Druk geeft de normale kracht per oppervlakte-eenheid op een gegeven punt aan, die op een gegeven vlak werkt. Aangezien er in een vloeistof in rust geen schuifspanningen aanwezig zijn – is de druk in een vloeistof onafhankelijk van de richting.
Voor vloeistoffen – vloeistoffen of gassen – in rust hangt de drukgradiënt in verticale richting alleen af van het soortelijk gewicht van de vloeistof.
Hoe de druk verandert met de hoogte in een vloeistof kan worden uitgedrukt als
Δp = – γ Δh (1)
waar
Δp = verandering van de druk (Pa, psi)
Δh = verandering in hoogte (m, in)
γ = soortelijk gewicht van vloeistof (N/m3, lb/ft3)
De drukgradiënt in verticale richting is negatief – de druk neemt naar boven toe af.
Specifiek gewicht
Het soortelijk gewicht van een vloeistof kan worden uitgedrukt als:
γ = ρ g (2)
waar
ρ = dichtheid van de vloeistof (kg/m3, slakken/ft3)
g = versnelling van de zwaartekracht (9.81 m/s2, 32.174 ft/s2)
In het algemeen is het soortelijk gewicht – γ – constant voor vloeistoffen. Voor gassen varieert het soortelijk gewicht – γ – met de hoogte (en de compressie).
De druk uitgeoefend door een statische vloeistof hangt slechts af van
- de diepte van de vloeistof
- de dichtheid van de vloeistof
- de versnelling van de zwaartekracht
Statische druk in een vloeistof
Voor een onsamendrukbare vloeistof – zoals een vloeistof – kan het drukverschil tussen twee hoogten worden uitgedrukt als:
Δp = p2 – p1
= – γ (h2 – h1) (3)
waar
p2 = druk op niveau 2 (Pa, psi)
p1 = druk op niveau 1 (Pa, psi)
h2 = niveau 2 (m, ft)
h1 = niveau 1 (m, ft)
(3) kan worden getransformeerd naar:
Δp = p1 – p2
= γ (h2 – h1) (4)
of
p1 – p2 = γ Δh (5)
waar
Δh = h2 – h1 = hoogteverschil – de diepte naar beneden van plaats h2 naar h1 (m, ft)
of
p1 = γ Δh + p2 (6)
Voorbeeld – Druk in een vloeistof
De absolute druk op een waterdiepte van 10 m kan worden berekend als:
p1 = γ Δh + p2
= (1000 kg/m3) (9,81 m/s2) (10 m) + (101.3 kPa)
= (98100 kg/ms2 of Pa) + (101300 Pa)
= 199400 Pa
= 199,4 kPa
waar
ρ = 1000 kg/m3
g = 9.81 m/s2
p2 = druk aan het oppervlak = atmosferische druk = 101,3 kPa
De overdruk kan worden berekend door p2 = 0
p1 = γ Δh + p2
= (1000 kg/m3) (9.81 m/s2) (10 m)
= 98100 Pa
= 98,1 kPa
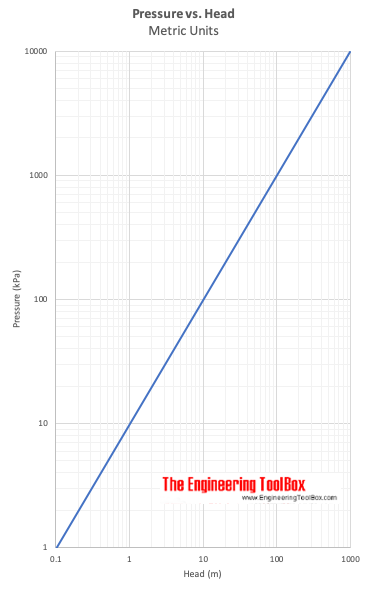
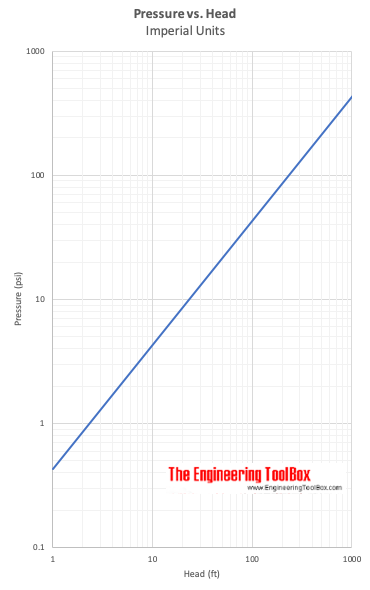
Druk vs. Opvoerhoogte
(6) kan worden omgezet in:
Δh = (p2 – p1) / γ (7)
Δh drukt de opvoerhoogte uit – het hoogteverschil van een kolom vloeistof met een bepaald gewicht – γ – dat nodig is om een drukverschil Δp = p2 – p1 te geven.
Voorbeeld – Druk vs. opvoerhoogte
Een drukverschil van 5 psi (lbf/in2) komt overeen met opvoerhoogte in water
(5 lbf/in2) (12 in/ft) (12 in/ft) / (62.4 lb/ft3)
= 11,6 ft water
of opvoerhoogte in kwik
(5 lbf/in2) (12 in/ft) (12 in/ft) / (847 lb/ft3)
= 0,85 ft kwik
Specifiek gewicht van water is 62.4 (lb/ft3) en het soortelijk gewicht van kwik is 847 (lb/ft3).
- Velocity – Dynamic Pressure vs. Head