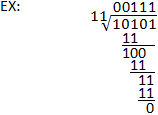Utilizați următoarele calculatoare pentru a efectua adunarea, scăderea, înmulțirea sau împărțirea a două valori binare, precum și pentru a converti valorile binare în valori zecimale și invers.

Calculație binară-adăugare, scădere, înmulțire, or Divide
Convert Binary Value to Decimal Value
Convert Decimal Value to Binary Value
Related Hex Calculator | IP Subnet Calculator
Sistemul binar este un sistem numeric care funcționează practic identic cu sistemul numeric zecimal cu care oamenii sunt probabil mai familiarizați. În timp ce sistemul numeric zecimal folosește numărul 10 ca bază, sistemul binar folosește 2. În plus, deși sistemul zecimal utilizează cifrele de la 0 la 9, sistemul binar utilizează doar 0 și 1, iar fiecare cifră este denumită bit. În afară de aceste diferențe, operațiile precum adunarea, scăderea, înmulțirea și împărțirea se calculează după aceleași reguli ca în sistemul zecimal.
Chiar toată tehnologia și calculatoarele moderne folosesc sistemul binar datorită ușurinței de implementare în circuitele digitale cu ajutorul porților logice. Este mult mai simplu să proiectezi hardware care trebuie să detecteze doar două stări, pornit și oprit (sau adevărat/false, prezent/absent etc.). Utilizarea unui sistem zecimal ar necesita un hardware care poate detecta 10 stări pentru cifrele de la 0 la 9 și este mai complicat.
Mai jos sunt câteva conversii tipice între valorile binare și cele zecimale:
Conversie binar/decimal
| Decimal | Binar |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 7 | 111 |
| 8 | 1000 |
| 10 | 1010 |
| 16 | 10000 |
| 20 | 10100 |
În timp ce lucrul cu binar poate părea inițial confuz, înțelegerea faptului că fiecare cifră binară reprezintă 2n, la fel cum fiecare cifră zecimală reprezintă 10n, ar trebui să ajute la clarificare. Să luăm de exemplu numărul 8. În sistemul numeric zecimal, 8 este poziționat în prima poziție zecimală din stânga punctului zecimal, însemnând locul 100. În esență, aceasta înseamnă:
8 × 100 = 8 × 1 = 8
Utilizând numărul 18 pentru comparație:
(1 × 101) + (8 × 100) = 10 + 8 = 18
În binar, 8 este reprezentat ca 1000. Citind de la dreapta la stânga, primul 0 reprezintă 20, al doilea 21, al treilea 22, iar al patrulea 23; la fel ca în sistemul zecimal, doar că are baza 2 și nu 10. Deoarece 23 = 8, se introduce un 1 în poziția sa, ceea ce dă 1000. Folosind 18, sau 10010 ca exemplu:
18 = 16 + 2 = 24 + 21
10010 = (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (0 × 20) = 18
Procesul pas cu pas pentru a converti din sistemul zecimal în sistemul binar este:
- Găsește cea mai mare putere de 2 care se află în interiorul numărului dat
- Suprimă această valoare din numărul dat
- Găsește cea mai mare putere de 2 în interiorul restului găsit la pasul 2
- Repeți până când nu mai există rest
- Introduceți un 1 pentru fiecare valoare de poziție binară găsită, și un 0 pentru restul
Utilizând din nou ținta de 18 ca exemplu, mai jos este un alt mod de a vizualiza acest lucru:
| 2n | 24 | 23 | 22 | 21 | 20 |
| Instanțe în limita a 18 | 1 | 0 | 0 | 1 | 0 |
| Țintă: 18 | 18 – 16 = 2 | → | 2 – 2 = 0 | ||
Conversia de la sistemul binar la cel zecimal este mai simplă. Determinați toate valorile locurilor în care apare 1 și găsiți suma valorilor.
EX: 10111 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 23
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 1 | 1 |
| 16 | 0 | 4 | 2 | 1 |
Înseamnă că: 16 + 4 + 4 + 2 + 1 = 23.
Adunare binară
Adunarea binară urmează aceleași reguli ca și adunarea în sistemul zecimal, cu excepția faptului că, în loc să se reporteze un 1 atunci când valorile adunate sunt egale cu 10, reportarea are loc atunci când rezultatul adunării este egal cu 2. Consultați exemplul de mai jos pentru clarificări.
Rețineți că în sistemul binar:
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, se reportează 1-ul, adică. 10
EX:
| 10 | 11 | 11 | 10 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | ||
| = | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Singura diferență reală între adunarea binară și cea zecimală este că valoarea 2 în sistemul binar este echivalentul lui 10 în sistemul zecimal. Rețineți că 1-ul supraevaluat reprezintă cifrele care sunt reportate. O greșeală frecventă la care trebuie să fim atenți atunci când efectuăm adunarea binară este în cazul în care 1 + 1 = 0 are, de asemenea, un 1 reportat din coloana anterioară din dreapta sa. Valoarea din partea de jos ar trebui să fie atunci 1 de la 1-ul reportat și nu 0. Acest lucru poate fi observat în a treia coloană din dreapta în exemplul de mai sus.
Substracție binară
În mod similar cu adunarea binară, există puține diferențe între scăderea binară și cea zecimală, cu excepția celor care decurg din utilizarea doar a cifrelor 0 și 1. Împrumutul apare în orice situație în care numărul care se scade este mai mare decât numărul din care se scade. În cazul scăderii binare, singurul caz în care împrumutul este necesar este atunci când se scade 1 din 0. Când se întâmplă acest lucru, 0-ul din coloana din care se împrumută devine, în esență, „2” (schimbând 0-1 în 2-1 = 1), reducând în același timp 1-ul din coloana din care se împrumută cu 1. Dacă următoarea coloană este, de asemenea, 0, împrumutul va trebui să aibă loc din fiecare coloană următoare până când o coloană cu valoarea 1 poate fi redusă la 0. Consultați exemplul de mai jos pentru clarificări.
Rețineți că în sistemul binar:
- 0 – 0 = 0
0 – 1 = 1, se împrumută 1, rezultând -1 reportat
1 – 0 = 1
1 – 1 = 0
EX1:
| -11 | 20 | 1 | 1 | 1 | |||
| – | 0 | 1 | 1 | 0 | 1 | ||
| = | 0 | 1 | 0 | 1 | 0 | 0 | |
EX2:
| -11 | 2-10 | 0 | |||
| – | 0 | 1 | 1 | ||
| = | 0 | 0 | 0 | 1 | |
Rețineți că suprapunctele afișate reprezintă modificările care se produc pe fiecare bit în cazul împrumutului. Coloana care împrumută obține, în esență, 2 în urma împrumutului, iar coloana de la care se împrumută este redusă cu 1.
Înmulțirea binară
Înmulțirea binară este, fără îndoială, mai simplă decât omologul său zecimal. Deoarece singurele valori utilizate sunt 0 și 1, rezultatele care trebuie adunate sunt fie identice cu primul termen, fie 0. Rețineți că, în fiecare rând următor, trebuie să se adauge 0-uri de rezervă, iar valoarea trebuie să fie deplasată spre stânga, la fel ca în cazul înmulțirii zecimale. Complexitatea înmulțirii binare provine din adunarea binară plictisitoare care depinde de numărul de biți din fiecare termen. Consultați exemplul de mai jos pentru clarificări.
Rețineți că în sistemul binar:
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
EX:
| 1 | 0 | 1 | 1 | 1 | ||||
| × | 1 | 1 | ||||||
| 1 | 0 | 1 | 1 | 1 | ||||
| + | 1 | 0 | 1 | 1 | 1 | 0 | ||
| = | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
Cum se poate observa în exemplul de mai sus, procesul de înmulțire binară este același cu cel al înmulțirii zecimale. Observați că simbolul 0 este scris în al doilea rând. În mod obișnuit, simbolul 0 nu este prezent vizual în cazul înmulțirii zecimale. Deși același lucru se poate face și în acest exemplu (cu simbolul 0 presupus și nu explicit), acesta este inclus în acest exemplu deoarece 0 este relevant pentru orice calculator de adunare/suprimare binară, precum cel furnizat pe această pagină. Fără ca 0-ul să fie afișat, ar fi posibil să se facă greșeala de a exclude 0-ul atunci când se adună valorile binare afișate mai sus. Rețineți din nou că, în sistemul binar, orice 0 aflat în dreapta unui 1 este relevant, în timp ce orice 0 aflat în stânga ultimului 1 din valoare nu este relevant.
EX:
- 1 0 1 0 1 0 1 1 0 0 0
= 0 0 1 0 1 0 1 1 1 0 0 0
≠ 1 0 1 0 1 1 1 0 0 0 0 0 0
Diviziune binară
Procesul de diviziune binară este similar diviziunii lungi din sistemul zecimal. Dividendul este în continuare împărțit la divizor în același mod, singura diferență semnificativă fiind utilizarea scăderii binare și nu a celei zecimale. Rețineți că o bună înțelegere a scăderii binare este importantă pentru efectuarea împărțirii binare. Consultați exemplul de mai jos, precum și secțiunea privind scăderea binară pentru clarificări.