Presiunea indică forța normală pe unitatea de suprafață într-un punct dat care acționează pe un plan dat. Deoarece nu există tensiuni de forfecare prezente într-un fluid în repaus – presiunea într-un fluid este independentă de direcție.
Pentru fluidele – lichide sau gaze – în repaus, gradientul de presiune pe direcție verticală depinde numai de greutatea specifică a fluidului.
Cum se modifică presiunea cu înălțimea într-un fluid se poate exprima prin
Δp = – γ Δh (1)
unde
Δp = variația presiunii (Pa, psi)
Δh = modificarea înălțimii (m, in)
γ = greutatea specifică a fluidului (N/m3, lb/ft3)
Gradientul de presiune în direcție verticală este negativ – presiunea scade în sus.
Puterea specifică
Puterea specifică a unui fluid poate fi exprimată astfel:
γ = ρ g (2)
unde
ρ = densitatea fluidului (kg/m3, melci/ft3)
g = accelerația gravitației (9.81 m/s2, 32,174 ft/s2)
În general, greutatea specifică – γ – este constantă pentru fluide. Pentru gaze, greutatea specifică – γ – variază în funcție de înălțime (și de compresie).
Δp = p2 – p1
= – γ (h2 – h1) (3)
unde
p2 = presiunea la nivelul 2 (Pa, psi)
p1 = presiunea la nivelul 1 (Pa, psi)
h2 = nivelul 2 (m, ft)
h1 = nivelul 1 (m, ft)
(3) poate fi transformat în:
Δp = p1 – p2
= γ (h2 – h1) (4)
sau
p1 – p2 = γ Δh (5)
unde
Δh = h2 – h1 = diferența de elevație – adâncimea în jos de la locația h2 la h1 (m, ft)
sau
p1 = γ Δh + p2 (6)
Exemplu – Presiunea într-un fluid
Presiunea absolută la o adâncime a apei de 10 m poate fi calculată astfel:
p1 = γ Δh + p2
= (1000 kg/m3) (9,81 m/s2) (10 m) + (101.3 kPa)
= (98100 kg/ms2 sau Pa) + (101300 Pa)
= 199400 Pa
= 199,4 kPa
unde
ρ = 1000 kg/m3
g = 9.81 m/s2
p2 = presiunea la nivelul suprafeței = presiunea atmosferică = 101,3 kPa
Presiunea manometrică poate fi calculată prin setarea p2 = 0
p1 = γ Δh + p2
= (1000 kg/m3) (9.81 m/s2) (10 m)
= 98100 Pa
= 98,1 kPa
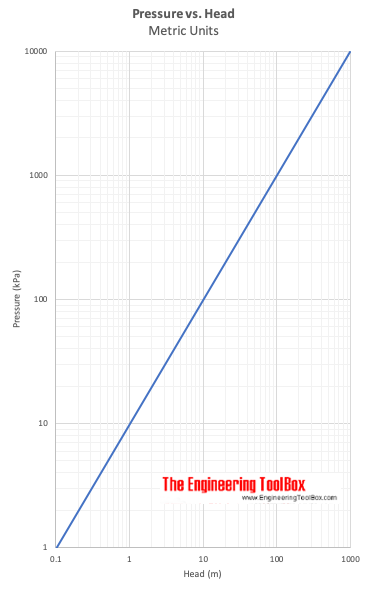
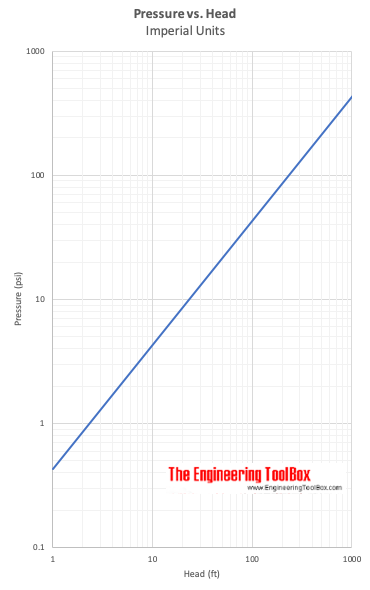
Presiunea în funcție de presiune. Capul
(6) poate fi transformat în:
Δh = (p2 – p1) / γ (7)
Δh exprimă capul – diferența de înălțime a unei coloane de fluid de greutate specifică – γ – necesară pentru a da o diferență de presiune Δp = p2 – p1.
Exemplu – Presiune vs. înălțime
O diferență de presiune de 5 psi (lbf/in2) este echivalentă cu înălțimea în apă
(5 lbf/in2) (12 in/ft) (12 in/ft) (12 in/ft) / (62.4 lb/ft3)
= 11,6 ft de apă
sau cap în mercur
(5 lbf/in2) (12 in/ft) (12 in/ft) (12 in/ft) / (847 lb/ft3)
= 0,85 ft de mercur
Greutatea specifică a apei este de 62.4 (lb/ft3) și greutatea specifică a mercurului este de 847 (lb/ft3).
- Velocitate – Presiune dinamică în funcție de înălțime

.