Amorterad analys används för algoritmer som har dyra operationer som endast sker sällan.

Amorterad analys av komplexitet används oftast med datastrukturer som har tillstånd som kvarstår mellan operationer.Den grundläggande idén är att en dyr operation kan ändra tillståndet så att det värsta fallet inte kan inträffa igen under lång tid, vilket gör att kostnaden amorteras.
Låt T1, T2, …, Tk vara komplexiteten hos en sekvens av operationer på en datastruktur. Den avskrivna komplexiteten för en enskild operation i denna sekvens är(T1 + T2 + …+ Tk) / k.
Exempel: en dynamisk matris
I en dynamisk matris lagras element i början av en underliggande fast matris och de återstående positionerna är oanvända.
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++Här är en bild av minnet när man lägger till elementen 2, 7, 1, 3, 8, 4till en ursprungligen tom matris med kapacitet 2.
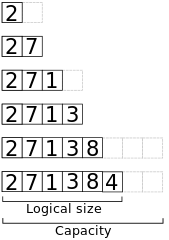
Svåraste tid
Den värsta tidskomplexiteten för att lägga till ett element till en matris med längd n, med hjälp av denna algoritm, är Θ(n).Om matrisen är full allokerar algoritmen en ny matris med längd 2n och kopierar sedan elementen från den gamla matrisen till den nya.
Det är tveksamt om detta resultat är alltför pessimistiskt.De följande n append-operationerna kommer att vara mycket billigare – var och en av dem kommer att köras på konstant tid eftersom den nyallokerade matrisen har plats för alla nya element.
Amorterad tid
En analys av den amorterade tiden ger en mycket bättre förståelse för algoritmen.
Konsultera en sekvens av n append-operationer,där vi börjar med en matris av längd 1. En noggrann analys visar att den totala tiden för dessa operationer endast är Θ(n).
- Det kommer att finnas totalt n tilldelnings- och inkrementeringsoperationer med konstant tid.
- Omstorleken kommer endast att ske vid operation 1, 2, 4, …, 2k, vilket ger totalt 1 + 2 + 4 + … + 2k = 2-2k – 1 elementkopieringsoperationer med konstant tid. Eftersom 2k ≤ n är detta högst 2n – 1.
Därmed är den avskrivna tidskomplexiteten för en enda append-operation Θ(1).
Mer om algoritmanalys

Tidskomplexitet: Räkna dina steg

Big O-notation