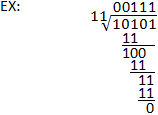Mit den folgenden Rechnern können Sie die Addition, Subtraktion, Multiplikation oder Division von zwei Binärwerten durchführen sowie Binärwerte in Dezimalwerte umwandeln und umgekehrt.

Binärberechnung – Addieren, Subtrahieren, Multiplizieren, oder dividieren
Binärwert in Dezimalwert umwandeln
Dezimalwert in Binärwert umwandeln
Verwandter Hex-Rechner | IP-Subnetz-Rechner
Das Binärsystem ist ein numerisches System, das praktisch identisch mit dem dezimalen Zahlensystem funktioniert, mit dem die Menschen wahrscheinlich besser vertraut sind. Während das Dezimalsystem die Zahl 10 als Basis verwendet, verwendet das Binärsystem die Zahl 2. Außerdem werden im Dezimalsystem die Ziffern 0 bis 9 verwendet, während im Binärsystem nur 0 und 1 verwendet werden, wobei jede Ziffer als Bit bezeichnet wird. Abgesehen von diesen Unterschieden werden Operationen wie Addition, Subtraktion, Multiplikation und Division nach denselben Regeln berechnet wie im Dezimalsystem.
Fast alle modernen Technologien und Computer verwenden das Binärsystem, weil es sich mit Hilfe von Logikgattern leicht in digitale Schaltungen implementieren lässt. Es ist viel einfacher, Hardware zu entwickeln, die nur zwei Zustände erkennen muss, nämlich an und aus (oder wahr/falsch, vorhanden/abwesend usw.). Die Verwendung eines Dezimalsystems würde Hardware erfordern, die 10 Zustände für die Ziffern 0 bis 9 erkennen kann, und das ist komplizierter.
Nachfolgend sind einige typische Umrechnungen zwischen binären und dezimalen Werten aufgeführt:
Binär/Dezimal Umrechnung
| Dezimal | Binär |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 7 | 111 |
| 8 | 1000 |
| 10 | 1010 |
| 16 | 10000 |
| 20 | 10100 |
Die Arbeit mit dem Binärsystem mag zunächst verwirrend erscheinen, Aber wenn man versteht, dass jede Binärstelle für 2n steht, so wie jede Dezimalstelle für 10n steht, sollte das zur Klärung beitragen. Nehmen wir zum Beispiel die Zahl 8. Im dezimalen Zahlensystem steht die 8 auf der ersten Dezimalstelle links vom Dezimalpunkt, also auf der 100er-Stelle. Das bedeutet im Wesentlichen:
8 × 100 = 8 × 1 = 8
Zum Vergleich die Zahl 18:
(1 × 101) + (8 × 100) = 10 + 8 = 18
Im Binärsystem wird die 8 als 1000 dargestellt. Von rechts nach links gelesen, steht die erste 0 für 20, die zweite für 21, die dritte für 22 und die vierte für 23; genau wie im Dezimalsystem, nur mit der Basis 2 statt 10. Da 23 = 8 ist, wird an dieser Stelle eine 1 eingegeben, was 1000 ergibt. Nehmen wir 18 oder 10010 als Beispiel:
18 = 16 + 2 = 24 + 21
10010 = (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (0 × 20) = 18
Das schrittweise Verfahren zur Umwandlung vom Dezimalsystem in das Binärsystem lautet
- Finde die größte 2er-Potenz, die innerhalb der gegebenen Zahl liegt
- Subtrahiere diesen Wert von der gegebenen Zahl
- Finde die größte 2er-Potenz innerhalb des in Schritt 2 gefundenen Restes
- Wiederhole den Vorgang, bis es keinen Rest mehr gibt
- Gebe für jeden gefundenen binären Stellenwert eine 1 ein, und eine 0 für den Rest
Am Beispiel der Zielzahl 18 lässt sich dies wie folgt veranschaulichen:
| 2n | 24 | 23 | 22 | 21 | 20 |
| Instanzen innerhalb 18 | 1 | 0 | 0 | 1 | 0 |
| Ziel: 18 | 18 – 16 = 2 | → | 2 – 2 = 0 | ||
Die Umrechnung vom Binär- ins Dezimalsystem ist einfacher. Bestimmen Sie alle Stellenwerte, an denen 1 vorkommt, und ermitteln Sie die Summe der Werte.
Z.B.: 10111 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 23
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 1 | 1 |
| 16 | 0 | 4 | 2 | 1 |
Daher: 16 + 4 + 2 + 1 = 23.
Binäre Addition
Die binäre Addition folgt denselben Regeln wie die Addition im Dezimalsystem, mit dem Unterschied, dass nicht eine 1 übertragen wird, wenn die addierten Werte gleich 10 sind, sondern dass übertragen wird, wenn das Ergebnis der Addition gleich 2 ist. Zur Verdeutlichung siehe das folgende Beispiel:
Beachten Sie, dass im Binärsystem:
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, Übertrag der 1, d.h. 10
EX:
| 10 | 11 | 11 | 10 | 1 | ||
| + | 1 | 0 | 1 | 1 | 1 | |
| = | 1 | 0 | 0 | 1 | 0 | 0 |
Der einzige wirkliche Unterschied zwischen binärer und dezimaler Addition besteht darin, dass der Wert 2 im binären System dem Wert 10 im dezimalen System entspricht. Beachten Sie, dass die hochgestellten 1en Ziffern darstellen, die übertragen werden. Ein häufiger Fehler, auf den man bei der binären Addition achten muss, ist der Fall, dass bei 1 + 1 = 0 auch eine 1 aus der vorhergehenden Spalte nach rechts übertragen wird. Der untere Wert sollte dann eine 1 sein, die sich aus der übertragenen 1 ergibt, und nicht eine 0. Dies ist in der dritten Spalte von rechts im obigen Beispiel zu beobachten.
Binäre Subtraktion
Wie bei der binären Addition gibt es auch bei der binären und dezimalen Subtraktion kaum Unterschiede, außer denen, die sich daraus ergeben, dass nur die Ziffern 0 und 1 verwendet werden. Eine Anleihe findet immer dann statt, wenn die Zahl, die subtrahiert wird, größer ist als die Zahl, von der sie abgezogen wird. Bei der binären Subtraktion ist eine Entlehnung nur dann notwendig, wenn 1 von 0 subtrahiert wird. In diesem Fall wird die 0 in der Entlehnungsspalte im Wesentlichen zu „2“ (die 0-1 wird zu 2-1 = 1), während die 1 in der Spalte, von der entlehnt wird, um 1 verringert wird. Wenn die folgende Spalte ebenfalls 0 ist, muss die Entlehnung von jeder nachfolgenden Spalte erfolgen, bis eine Spalte mit dem Wert 1 auf 0 reduziert werden kann. Zur Verdeutlichung wird auf das folgende Beispiel verwiesen.
Beachten Sie, dass im binären System:
- 0 – 0 = 0
0 – 1 = 1, leihen Sie sich 1, was zu einer übertragenen -1 führt
1 – 0 = 1
1 – 1 = 0
EX1:
| -11 | 20 | 1 | 1 | 1 | ||
| – | 0 | 1 | 1 | 0 | 1 | |
| = | 0 | 1 | 0 | 1 | 0 | |
EX2:
| -11 | 2-10 | 0 | ||
| – | 0 | 1 | 1 | |
| = | 0 | 0 | 1 | |
Beachten Sie, dass die angezeigten Hochkommata die Änderungen sind, die an jedem Bit beim Borgen auftreten. Die ausleihende Spalte erhält durch das Ausleihen im Wesentlichen eine 2, und die Spalte, von der ausgeliehen wird, wird um 1 verringert.
Binäre Multiplikation
Die binäre Multiplikation ist wohl einfacher als ihr dezimales Gegenstück. Da nur die Werte 0 und 1 verwendet werden, sind die Ergebnisse, die addiert werden müssen, entweder gleich dem ersten Term oder 0. Beachten Sie, dass in jeder folgenden Zeile Platzhalter 0 hinzugefügt und der Wert nach links verschoben werden muss, genau wie bei der Dezimalmultiplikation. Die Komplexität der binären Multiplikation ergibt sich aus der mühsamen binären Addition, die davon abhängt, wie viele Bits in jedem Term enthalten sind. Zur Verdeutlichung siehe das folgende Beispiel:
Beachten Sie, dass im Binärsystem:
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
EX:
| 1 | 0 | 1 | 1 | 1 | |||
| × | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | 0 | |
| = | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
Wie im obigen Beispiel zu sehen ist, ist der Prozess der binären Multiplikation derselbe wie bei der dezimalen Multiplikation. Beachten Sie, dass der Platzhalter 0 in die zweite Zeile geschrieben wird. Bei der dezimalen Multiplikation ist der Platzhalter 0 normalerweise nicht sichtbar. Obwohl dies auch in diesem Beispiel möglich ist (wobei der 0-Platzhalter nicht explizit, sondern angenommen wird), wird er in diesem Beispiel aufgeführt, da die 0 für jeden binären Additions-/Subtraktionsrechner, wie den auf dieser Seite bereitgestellten, relevant ist. Ohne die Anzeige der 0 wäre es möglich, bei der Addition der oben dargestellten binären Werte den Fehler zu machen, die 0 auszuschließen. Beachten Sie nochmals, dass im Binärsystem jede 0 rechts von einer 1 relevant ist, während jede 0 links von der letzten 1 im Wert nicht relevant ist.
EX:
- 1 0 1 0 1 1 0 0
= 0 0 1 0 1 0 1 1 0 0
≠ 1 0 1 0 1 0 0 0
Binäre Division
Das Verfahren der binären Division ist ähnlich wie die lange Division im Dezimalsystem. Der Dividend wird immer noch auf die gleiche Weise durch den Divisor dividiert, der einzige wesentliche Unterschied ist die Verwendung der binären statt der dezimalen Subtraktion. Beachten Sie, dass ein gutes Verständnis der binären Subtraktion wichtig für die Durchführung der binären Division ist. Siehe das folgende Beispiel sowie den Abschnitt über die binäre Subtraktion zur Erläuterung.