Der Druck gibt die Normalkraft pro Flächeneinheit an einem bestimmten Punkt an, die auf eine bestimmte Ebene wirkt. Da in einem ruhenden Fluid keine Scherspannungen vorhanden sind, ist der Druck in einem Fluid richtungsunabhängig.
Bei ruhenden Fluiden – Flüssigkeiten oder Gasen – hängt das Druckgefälle in vertikaler Richtung nur vom spezifischen Gewicht des Fluids ab.
Wie sich der Druck in einer Flüssigkeit mit der Höhe ändert, kann wie folgt ausgedrückt werden
Δp = – γ Δh (1)
wobei
Δp = Druckänderung (Pa, psi)
Δh = Höhenänderung (m, in)
γ = spezifisches Gewicht der Flüssigkeit (N/m3, lb/ft3)
Der Druckgradient in vertikaler Richtung ist negativ – der Druck nimmt nach oben ab.
Spezifisches Gewicht
Das spezifische Gewicht einer Flüssigkeit kann wie folgt ausgedrückt werden:
γ = ρ g (2)
wobei
ρ = Dichte der Flüssigkeit (kg/m3, slugs/ft3)
g = Erdbeschleunigung (9.81 m/s2, 32.174 ft/s2)
Im Allgemeinen ist das spezifische Gewicht – γ – für Flüssigkeiten konstant. Bei Gasen variiert das spezifische Gewicht – γ – mit der Höhe (und der Kompression).
Der von einem statischen Fluid ausgeübte Druck hängt nur ab von
- der Tiefe des Fluids
- der Dichte des Fluids
- der Erdbeschleunigung
Statischer Druck in einem Fluid
Für ein inkompressibles Fluid – wie eine Flüssigkeit – kann die Druckdifferenz zwischen zwei Höhenlagen ausgedrückt werden als:
Δp = p2 – p1
= – γ (h2 – h1) (3)
wobei
p2 = Druck in Höhe 2 (Pa, psi)
p1 = Druck in Höhe 1 (Pa, psi)
h2 = Niveau 2 (m, ft)
h1 = Niveau 1 (m, ft)
(3) kann transformiert werden zu:
Δp = p1 – p2
= γ (h2 – h1) (4)
oder
p1 – p2 = γ Δh (5)
wobei
Δh = h2 – h1 = Höhenunterschied – die Tiefe von Ort h2 nach h1 (m, ft)
oder
p1 = γ Δh + p2 (6)
Beispiel – Druck in einer Flüssigkeit
Der absolute Druck in einer Wassertiefe von 10 m kann berechnet werden als:
p1 = γ Δh + p2
= (1000 kg/m3) (9,81 m/s2) (10 m) + (101.3 kPa)
= (98100 kg/ms2 oder Pa) + (101300 Pa)
= 199400 Pa
= 199,4 kPa
wobei
ρ = 1000 kg/m3
g = 9.81 m/s2
p2 = Druck an der Oberfläche = Atmosphärendruck = 101,3 kPa
Der Überdruck kann berechnet werden, indem man p2 = 0
p1 = γ Δh + p2
= (1000 kg/m3) (9.81 m/s2) (10 m)
= 98100 Pa
= 98,1 kPa
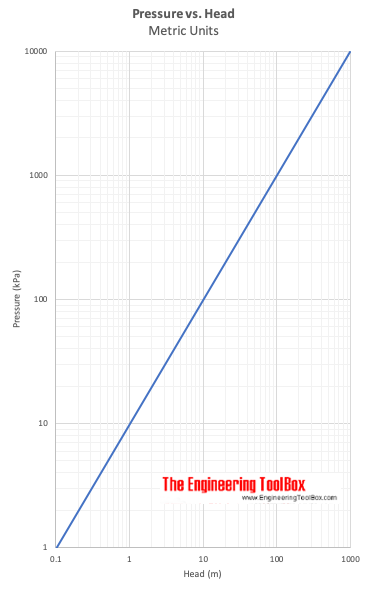
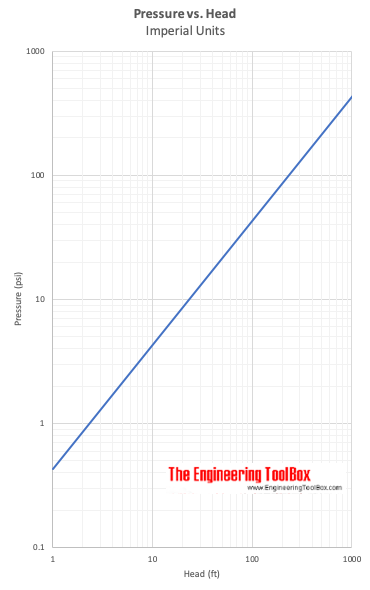
Druck vs. Druckhöhe
(6) kann umgewandelt werden in:
Δh = (p2 – p1) / γ (7)
Δh drückt die Druckhöhe – die Höhendifferenz einer Flüssigkeitssäule mit spezifischem Gewicht γ – aus, die erforderlich ist, um eine Druckdifferenz Δp = p2 – p1 zu erzeugen.
Beispiel – Druck vs. Förderhöhe
Eine Druckdifferenz von 5 psi (lbf/in2) entspricht einer Förderhöhe in Wasser
(5 lbf/in2) (12 in/ft) (12 in/ft) / (62.4 lb/ft3)
= 11.6 ft Wasser
oder Förderhöhe in Quecksilber
(5 lbf/in2) (12 in/ft) (12 in/ft) / (847 lb/ft3)
= 0.85 ft Quecksilber
Das spezifische Gewicht von Wasser ist 62.4 (lb/ft3) und das spezifische Gewicht von Quecksilber ist 847 (lb/ft3).
- Geschwindigkeit – Dynamischer Druck vs. Höhe