
Fern
Aquí hay una pregunta reciente del lector Pehr de Suecia:
Hola,
En primer lugar, maravilloso sitio. Me encanta.
He estado estudiando la sección de coordenadas polares con la esperanza de ampliar mis conocimientos sobre la espiral equiangular. Las herramientas interactivas son geniales, aunque me está costando derivar la solución matemática exacta de por qué la función resultante para la espiral áurea es
r = ae^(b(theta))
Para algunos antecedentes de la pregunta de Pehr, ver:
Coordenadas polares, curvas en coordenadas polares y espiral equiangular
Las espirales son comunes en la naturaleza y han inspirado a los matemáticos durante siglos.

Espiral de la sábila

Galaxia espiral NGC 5194
Espirales logarítmicas
La Espiral Dorada por la que pregunta Pehr es un caso especial de la espiral logarítmica.
Las espirales logarítmicas crecen de tal manera que el ángulo de una línea desde el centro de la espiral hasta la tangente a la curva en ese punto es constante. Por eso se conocen también como espirales «equi-angulares».
Para ver lo que esto significa, los 3 ángulos agudos marcados en la siguiente imagen del helecho son de aproximadamente 80°

Helecho equi-angular
Normalmente utilizamos funciones en Coordenadas Polares cuando describimos espirales. De lo contrario, si utilizamos coordenadas rectangulares ordinarias, las fórmulas se vuelven muy complejas.
La fórmula para una espiral logarítmica utilizando coordenadas polares es:
r = aeθ cot b
donde
r es la distancia al origen (o «polo»)
a es una constante
θ es el ángulo (en radianes) respecto al eje horizontal. Así que las coordenadas de un punto de la curva en coordenadas polares viene dado por (r, θ).
b es el ángulo (en radianes – el ángulo «igual») que forma la línea del centro de la espiral con la tangente a la espiral. En el caso del helecho anterior, b ≈ 1,4 radianes (≈ 80°).
Como consecuencia de la forma en que definimos la espiral logarítmica, la relación de las distancias del centro a cada brazo de la espiral de un par adyacente es constante.

Brazos de la espiral a una relación constante
La relación
distancia al primer brazo: distancia al segundo brazo
= 29:69
≈ 0.42
La otra relación
distancia al segundo brazo: distancia al tercer brazo
= 69:154
≈ 0,45
Vemos que las relaciones son casi iguales. (En una espiral logarítmica real, son exactamente iguales. Elegir el punto de inicio del helecho no es una ciencia exacta).
Espiral dorada
La espiral dorada es un caso especial de la espiral logarítmica.
Podemos escribir la espiral logarítmica general como una función en coordenadas polares usando t de la siguiente manera:
r(t) = aet cot b
Nota: Normalmente, usamos θ para la variable independiente, pero a menudo usamos t ya que podemos pensar que la espiral se traza en el tiempo. Además, ¡es más fácil de escribir!
La espiral áurea tiene la propiedad especial de que por cada 1/4 de vuelta (90° o π/2 en radianes), la distancia desde el centro de la espiral aumenta en la proporción áurea φ = 1,6180.
Para que esto ocurra, cot b debe tomar el valor (que sale de resolver nuestra función):
![]()
Usando este valor, y tomando el caso simple en el que a = 1, nuestra función se convierte en:
r(t) = e0,30635t
A partir de aquí utilizaremos la excelente herramienta gráfica gratuita GeoGebra.
Configuración de la espiral áurea con GeoGebra
Ahora, si graficamos nuestra función en ejes de coordenadas rectangulares ordinarios en GeoGebra, obtenemos la siguiente curva exponencial. Obsérvese que r aumenta a un ritmo cada vez mayor (se hace más pronunciado) a medida que aumenta t.
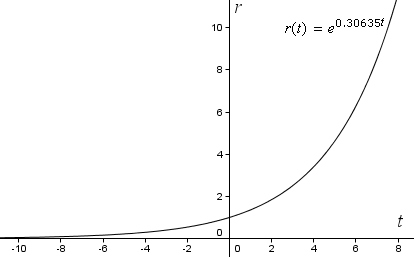
Pero para ver una espiral, necesitamos graficar la curva usando coordenadas polares.
Para convertir la forma polar (que tenemos) en forma rectangular (que necesitamos para la gráfica) en Geogebra, necesitamos establecer y graficar la siguiente función:
a(t) = (r(t) cos(t), r(t) sin(t))
Sustituyamos algunos valores importantes para ver qué significa esta expresión. Partiendo de t = 0, obtenemos el punto inicial de la curva:
a(0) = (r(0) cos(0), r(0) sin(0))
= (1×1, 1×0)
= (1, 0)
Entonces significa que empezamos a 1 unidad del origen a lo largo del eje x positivo. Puedes ver el punto de partida en la siguiente gráfica de la espiral.
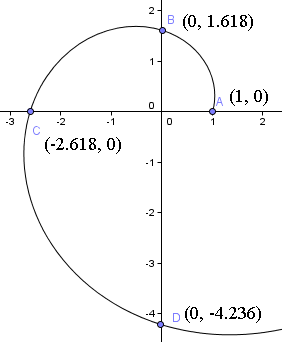
A continuación, giramos un cuarto de vuelta y encontramos en t = π/2,
a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2))
= (1,618×0, 1,618×1)
= (0, 1,618)
Nota que ahora estamos a 1,618 unidades del origen por el eje y. Es decir, φ = 1,6180 veces la distancia de la que partimos.
Otra rotación de un cuarto de vuelta nos lleva a t = π, donde:
a(π) = (r(π) cos(π), r(π) sin(π))
= (-2,618×1, -2,618×0)
= (-2,618, 0)
Ahora estamos a 2,618 unidades del origen a lo largo del eje x negativo, o φ = 1,6180 veces la distancia al origen que teníamos en el último cuarto de vuelta.
Nota:
φ2 = 2,6180
Podemos calcular nuestra siguiente posición, a lo largo del eje y negativo, simplemente multiplicando este último valor por φ = 1,6180, lo que nos da:
φ3 = 4,23606…
Así que la espiral cortará el eje y en (0, -4,236).
Un cuarto de vuelta más nos llevará a φ4 = 6,85410… unidades a lo largo del eje y positivo, es decir (6,854, 0).
Podemos ver que estos valores son correctos en nuestra gráfica de la espiral anterior.
Si seguimos adelante, obtendremos una espiral como la siguiente (se trata de 2 revoluciones completas, o 4π = 720°):
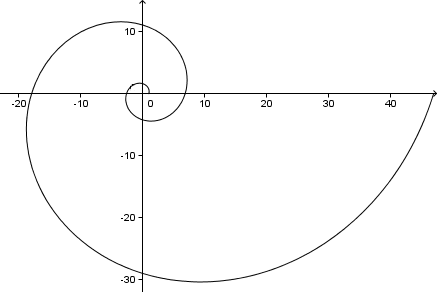
Como apunte, ya que en este problema
cot b = 0.30635
entonces
b = arccot 0,30635 = 1,274 radianes o unos 73°
Este es el ángulo que forman nuestros brazos de la espiral con una línea del centro de la misma. Puedes ver en el gráfico anterior que cada brazo de la espiral forma un ángulo de 73° con el eje x (y con el eje y, o con cualquier línea desde el centro).
Aproximación a la espiral áurea utilizando arcos de círculo
Podemos obtener una espiral que se parece bastante a la espiral áurea utilizando arcos de círculos que aumentan de tamaño por la razón áurea, como sigue.
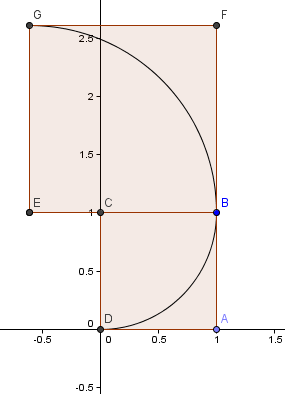
Empezamos con un cuadrado de 1×1 y dibujamos un arco, centro C, a través de 2 esquinas tal que los lados del cuadrado son tangentes al arco (es decir, se tocan una sola vez).
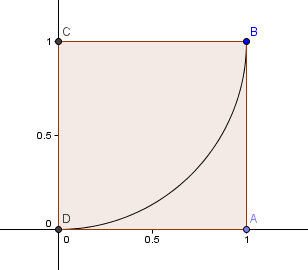
A continuación, colocamos un cuadrado con longitud de lado φ = 16180 por encima de nuestro primer cuadrado y construimos otro arco circular, centro E, como antes:
Nuestro siguiente cuadrado va a la izquierda y tiene lados φ2 = 2,6180 = 1 + φ.
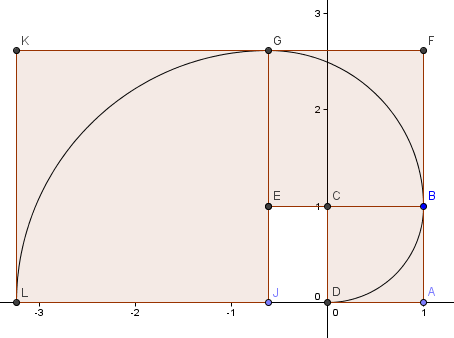
Continuamos el patrón (hemos dado otra vuelta completa) y obtenemos una espiral que se parece bastante a nuestra Espiral Dorada de antes.
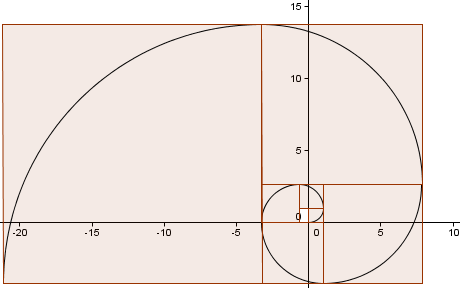
¿Qué tan cercana es nuestra aproximación?
El artículo de Wikipedia sobre la Espiral Dorada tiene una imagen que afirma que la espiral anterior y la Espiral Dorada tienen una forma muy cercana.
Aquí está esa imagen:
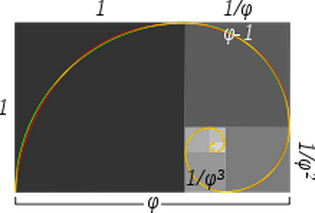
El pie de foto de la imagen dice:
Espirales doradas aproximada y verdadera: la espiral verde está hecha de cuartos de círculo tangentes al interior de cada cuadrado, mientras que la espiral roja es una espiral dorada, un tipo especial de espiral logarítmica. Las partes superpuestas aparecen en amarillo. La longitud del lado de un cuadrado mayor al siguiente más pequeño está en la proporción áurea.
¿Podemos recrear esto?
En la imagen de abajo, la curva roja es la primera parte de la espiral áurea que construimos anteriormente, mientras que la curva verde se basa en la aproximación del cuarto de vuelta que acabamos de trabajar.
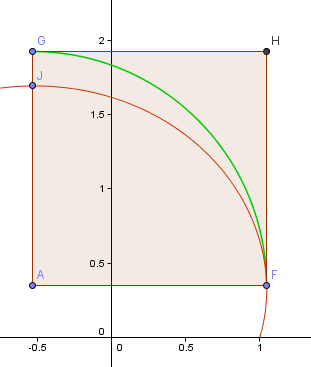
El punto F es el punto «más a la derecha» de la espiral, que será mi punto de partida para el arco del cuarto de vuelta. El punto J es el punto más alto de esta porción de la espiral.
El punto A es la intersección de las líneas horizontales y verticales que pasan por F y J respectivamente y este será el centro de mi arco.
Ahora, el arco GF no está en absoluto cerca de la porción relacionada de la espiral FJ.
Hagamos otro paso y veamos si la siguiente parte es mejor.
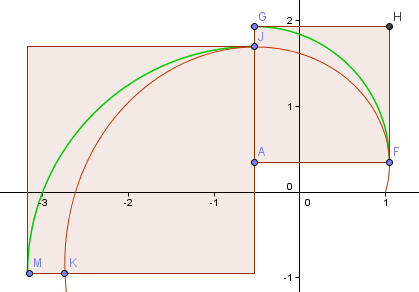
Como puedes ver, es peor (como era de esperar, ya que nos hemos alejado del origen y el brazo de la espiral es cada vez mayor).
Está claro que esto no va a funcionar nunca.
Sin embargo, en mi anterior Espiral Dorada utilizaba:
r(t) = e0.30635t
La constante a, tenía valor 1.
Si queremos que nuestros arcos de aproximación se ajusten bien a la Espiral Dorada real, tenemos que utilizar un valor de (probablemente no sorprendente)
a = φ = 1,618103399..
Esto nos da las siguientes curvas, similares al gráfico de Wikipedia.
La curva roja es la Espiral Dorada,
r(t) = 1,618013 e0,30635t
La curva verde es la colección de arcos circulares.
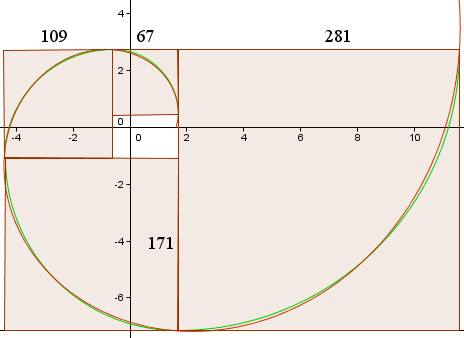
Se muestra la longitud de los lados de los cuadrados (en píxeles) y podemos ver que están aproximadamente en la proporción 1,618013…
Espiral dorada en el medio
De Wolfram’s Mathworld:
En el episodio de la cuarta temporada «Masterpiece» (2008) del drama criminal de la CBS-TV «Criminal Minds», los agentes de la Unidad de Análisis del Comportamiento del FBI se enfrentan a un asesino en serie que utiliza la secuencia numérica de Fibonacci para determinar el número de víctimas de cada uno de sus episodios de asesinato. En este episodio, el personaje Dr. Reid también se da cuenta de que las ubicaciones de los asesinatos se encuentran en el gráfico de una espiral dorada, e ir al centro de la espiral permite a Reid determinar la ubicación de la base de operaciones del asesino.
Aquí hay más información interesante de Wolfram’s Mathworld:
Espiral logarítmica
Para los geeks – diseño con espiral áurea
Se cree que los diseños que utilizan la proporción áurea y la espiral áurea son agradables a la vista.
Incluso Twitter ha rediseñado recientemente su página principal utilizando la espiral áurea.
Aquí hay un gran artículo de un tipo que ha construido una espiral dorada sin imágenes. (Sobre todo para los interesados en el diseño web)
Espiral dorada sin imágenes – usando CSS y jQuery
Como sugiere en el artículo, la trompa de un elefante también se acerca a la Espiral Dorada.

Trompa de elefante – casi una Espiral de Oro
Conclusión
La Espiral de Oro es un tema interesante – uno que vale la pena perseguir no sólo por los diseños agradables involucrados, sino también la interesante matemática detrás de ellos.
¡Espero que esto ayude a responder a tu pregunta, Pehr!