
Fern
Itt egy friss kérdés a svédországi Pehr olvasótól:
Hi,
Először is, csodálatos oldal. Imádom.
A polárkoordinátákról szóló részt tanulmányoztam, remélve, hogy bővíthetem a tudásomat az egyenlőszögű spirálról. Az interaktív eszközök nagyszerűek, bár nehezen tudom levezetni a pontos matematikai megoldást arra, hogy miért
r = ae^(b(theta)) az arany spirál eredő függvénye.
Pehr kérdésének hátterét lásd:
Poláris koordináták, görbék poláris koordinátákban és egyenlő szögű spirál
A spirálok gyakoriak a természetben, és évszázadok óta inspirálják a matematikusokat.

Aloe spirál

Spirál galaxis NGC 5194
Logaritmikus spirál
A Pehr által kérdezett Arany spirál a logaritmikus spirál egy speciális esete.
A logaritmikus spirálok úgy nőnek, hogy a spirál középpontja és a görbe adott ponton lévő érintője közötti egyenes szöge állandó. Ezért nevezik őket “egyenlő szögű” spiráloknak is.
Hogy lássuk, mit jelent ez, az alábbi páfrányképen jelölt 3 hegyesszög körülbelül 80°

Egyenlő szögű páfrány
A spirálok leírásakor általában polárkoordinátákban megadott függvényeket használunk. Ellenkező esetben, ha közönséges derékszögű koordinátákat használunk, a képletek nagyon bonyolulttá válnak.
A logaritmikus spirál képlete polárkoordinátákat használva a következő:
r = aeθ cot b
ahol
r az origótól (vagy “pólustól”) mért távolság
a egy állandó
θ a vízszintes tengelytől mért szög (radiánban). Tehát a görbe egy pontjának koordinátáit polárkoordinátákban (r, θ) adja meg.
b az a szög (radiánban – az “egyenlő” szög), amelyet a spirál középpontjából kiinduló egyenes a spirál érintőjével bezár. A fenti páfrányfenyő esetében b ≈ 1,4 radián (≈ 80°).
A logaritmikus spirál meghatározásának módjából következik, hogy egy szomszédos pár egyes spirálkarjainak középpontjától mért távolságok aránya állandó.

Spirálkarok állandó arányban
Az első kar távolsága
:második kar távolsága
= 29:69
≈ 0.42
A másik arány
távolság a második kartól: távolság a harmadik kartól
= 69:154
≈ 0,45
Láthatjuk, hogy az arányok közel azonosak. (Egy tényleges logaritmikus spirálban pontosan megegyeznek. A páfrány spirál kezdőpontjának kiválasztása nem egzakt tudomány!)
Aranyspirál
Az aranyspirál a logaritmikus spirál egy speciális esete.
Az általános logaritmikus spirált a következőképpen írhatjuk fel függvényként polárkoordinátákban t segítségével:
r(t) = aet cot b
Megjegyzés: Általában θ-t használjuk a független változónak, de gyakran t-t használunk, mivel a spirál időbeli követésére gondolhatunk. Különben is, könnyebb beírni!
Az aranyspirálnak olyan különleges tulajdonsága van, hogy minden 1/4 fordulat (90° vagy π/2 radiánban) esetén a spirál középpontjától mért távolság a φ = 1,6180 aranymetszéssel nő.
Ezért a cot b értéket kell felvennie (ami a függvényünk megoldásából származik):
![]()
Ezt az értéket felhasználva, és azt az egyszerű esetet véve, amikor a = 1, a függvényünk a következő lesz:
r(t) = e0.30635t
A továbbiakban a kiváló ingyenes grafikus eszközt, a GeoGebrát fogjuk használni.
Az aranyspirál felállítása a GeoGebra segítségével
Ha most a GeoGebrában ábrázoljuk függvényünket a közönséges derékszögű koordinátatengelyeken, a következő exponenciális görbét kapjuk. Vegyük észre, hogy az r egyre nagyobb ütemben növekszik (meredekebbé válik), ahogy t növekszik.
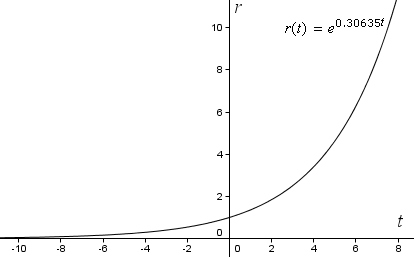
De ahhoz, hogy spirált lássunk, a görbét polárkoordinátákkal kell ábrázolnunk.
Azért, hogy a Geogebrában a polárformát (ami megvan) átkonvertáljuk derékszögű formára (amire a grafikonhoz szükségünk van), a következő függvényt kell felállítanunk és ábrázolnunk:
a(t) = (r(t) cos(t), r(t) sin(t))
Helyettesítsünk be néhány fontos értéket, hogy lássuk, mit jelent ez a kifejezés. A t = 0-ból kiindulva megkapjuk a görbe kezdőpontját:
a(0) = (r(0) cos(0), r(0) sin(0))
= (1×1, 1×0)
= (1, 0)
Ez tehát azt jelenti, hogy a pozitív x tengely mentén az origótól 1 egységnyire indulunk. A kiindulópontot a spirál következő grafikonján láthatjuk.
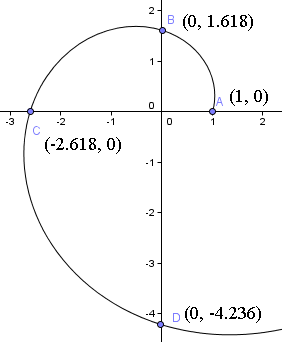
A következőkben elforgatunk egy negyed fordulatot, és t = π/2-nél találjuk,
a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2))
= (1,618×0, 1,618×1)
= (0, 1,618)
Megjegyezzük, hogy most 1,618 egységnyire vagyunk az origótól az y tengelyen felfelé. Vagyis φ = a kiindulási távolság 1,6180-szorosa.
Egy újabb negyed fordulatos elforgatással elérjük a t = π értéket, ahol:
a(π) = (r(π) cos(π), r(π) sin(π))
= (-2,618×1, -2,618×0)
= (-2,618, 0)
Most 2,618 egységnyire vagyunk az origótól a negatív x tengely mentén, vagy φ = 1,6180-szorosa annak a távolságnak, amennyire az origótól az utolsó negyed fordulatnál voltunk.
Jegyzet:
φ2 = 2,6180
A következő helyzetünket, a negatív y-tengely mentén, kiszámíthatjuk úgy, hogy ezt az utolsó értéket egyszerűen megszorozzuk φ = 1,6180-zal, így kapjuk:
φ3 = 4,23606…
A spirál tehát az y-tengelyt a (0, -4,236) ponton fogja metszeni.
Még egy negyed fordulat és elérjük a φ4 = 6,85410… egységet a pozitív y-tengely mentén, azaz (6,854, 0).
A fenti spirálgrafikonunkon láthatjuk, hogy ezek az értékek helyesek.
Ha továbbmegyünk, akkor a következő spirált kapjuk (ez 2 teljes fordulat, vagy 4π = 720°):
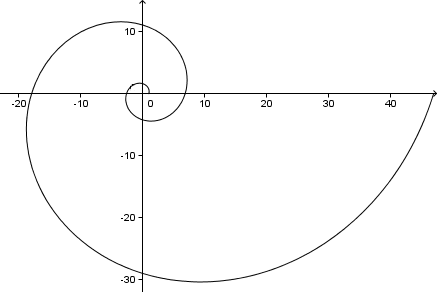
Mellesleg, mivel ebben a feladatban
cot b = 0.30635
akkor
b = arccot 0,30635 = 1,274 radián vagy kb. 73°
Ez az a szög, amit a spirálkarunk a spirál középpontjából kiinduló egyenessel bezár. A fenti grafikonon láthatjuk, hogy minden spirálkar 73°-os szöget zár be az x-tengellyel (és az y-tengellyel, vagy a középpontból kiinduló bármely vonallal).
Az aranyspirál megközelítése körívek segítségével
Az aranyspirálhoz nagyon hasonló spirált kaphatunk, ha olyan köríveket használunk, amelyek mérete az aranymetszéssel nő, az alábbiak szerint.
Egy 1×1-es négyzettel kezdünk, és rajzolunk egy ívet, C középponttal, 2 sarkon keresztül úgy, hogy a négyzet oldalai az ívet érintsék (vagyis csak egyszer érintsék egymást).
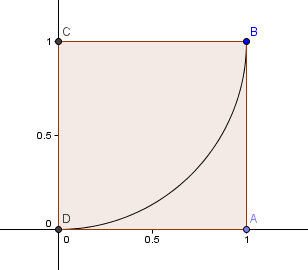
A következő lépésben egy φ = 1 oldalhosszúságú négyzetet helyezünk el.6180 az első négyzetünk fölé, és konstruálunk egy újabb körívet, középpontja E, mint korábban:
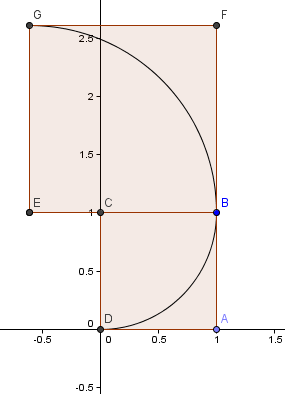
A következő négyzetünk balra kerül, és oldalhosszúsága φ2 = 2,6180 = 1 + φ.
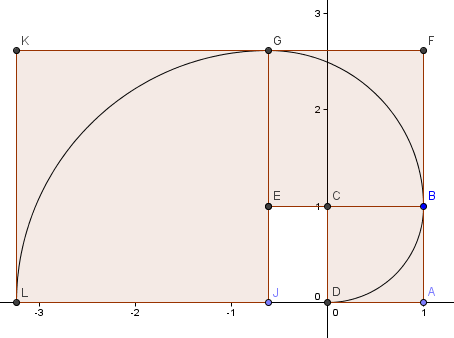
Folytatjuk a mintát (egy újabb teljes kört mentünk), és egy olyan spirált kapunk, amely nagyon hasonlít a korábbi Arany-spirálunkhoz.
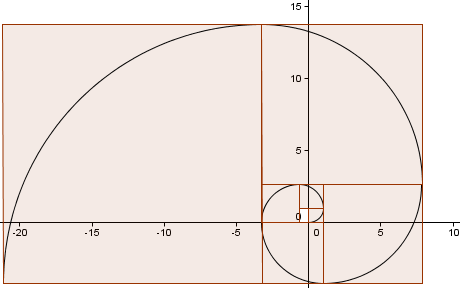
Mennyire közelítjük meg?
A Wikipedia Arany-spirál szócikkében van egy kép, amely azt állítja, hogy a fenti spirál és az Arany-spirál nagyon közel állnak egymáshoz.
Itt van ez a kép:
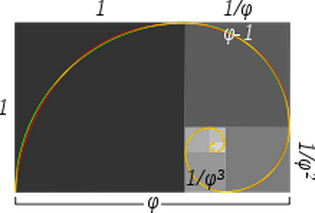
A kép felirata szerint:
Megközelítő és valódi aranyspirál: a zöld spirál az egyes négyzetek belsejét érintő negyedkörökből áll, míg a piros spirál egy aranyspirál, a logaritmikus spirál egy speciális típusa. Az átfedő részek sárgának tűnnek. Egy nagyobb négyzet oldalának a következő kisebb négyzethez viszonyított hossza az aranymetszésben van.
Meg tudjuk ezt újraalkotni ?
A lenti képen a piros görbe a fentebb konstruált aranyspirál első része, míg a zöld görbe a negyedkörös közelítésen alapul, amin az imént dolgoztunk.
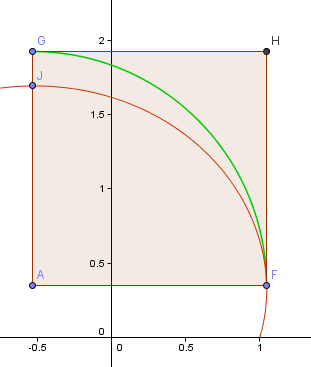
Az F pont a spirál “legjobb” pontja, ami a negyedkörös ív kiindulópontja lesz számomra. A J pont a spirál ezen részének legmagasabb pontja.
A pont az F-en és J-n áthaladó vízszintes és függőleges egyenesek metszéspontja, és ez lesz az ívem középpontja.
A GF ív most egyáltalán nem áll közel a spirál FJ kapcsolódó részéhez.
Tegyünk még egy lépést, és nézzük meg, hogy a következő rész jobb-e.
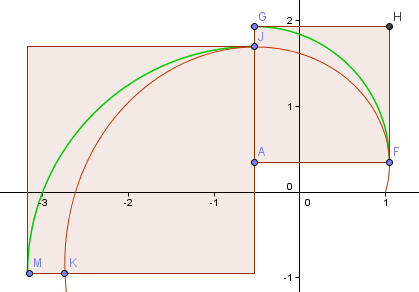
Mint láthatjuk, rosszabb lett (ahogy várható volt, hiszen távolabb kerültünk az origótól, és a spirálkar egyre nagyobb).
Láthatóan ez soha nem fog működni.
Mégis a korábbi Aranyspirálomban használtam:
r(t) = e0.30635t
A konstans a, értéke 1 volt.
Ha azt akarjuk, hogy a közelítő íveink jól illeszkedjenek a tényleges Aranyspirálhoz, akkor (valószínűleg nem meglepő módon)
a = φ = 1.618103399 értéket kell használnunk…
Az alábbi görbéket kapjuk, hasonlóan a Wikipédiában található grafikonhoz.
A piros görbe az Aranyspirál,
r(t) = 1,618013 e0,30635t
A zöld görbe a körívek gyűjteménye.
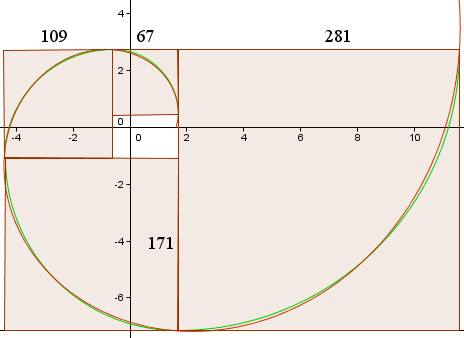
A négyzetek oldalhossza (pixelben) látható, és láthatjuk, hogy megközelítőleg 1,618013 arányban vannak…
Az Aranyspirál a médiában
From Wolfram’s Mathworld:
A CBS televízió Criminal Minds című bűnügyi drámájának 4. évadának “Masterpiece” (2008) című epizódjában az FBI viselkedéselemző egységének ügynökei egy sorozatgyilkossal kerülnek szembe, aki a Fibonacci-számsorozatot használja arra, hogy meghatározza az egyes gyilkossági epizódjai áldozatainak számát. Ebben az epizódban a karakter Dr. Reid azt is észreveszi, hogy a gyilkosságok helyszínei egy arany spirál grafikonján helyezkednek el, és a spirál közepére haladva Reid meg tudja határozni a gyilkos bázisának helyét.
Itt még több érdekes információ a Wolfram’s Mathworldből:
Logaritmikus spirál
A kockáknak – design az aranyspirállal
Sokak szerint az aranymetszést és az aranyspirált használó design kellemes a szemnek.
Még a Twitter is az aranyspirál segítségével tervezte át nemrég a főoldalát.
Itt van egy nagyszerű cikk egy fickótól, aki képek nélkül konstruált egy arany spirált. (Főleg a webdesign iránt érdeklődőknek)
Az arany spirál képek nélkül – CSS és jQuery segítségével
A cikk szerint az elefánt ormánya is közel áll az arany spirálhoz.

Elefánt ormány – majdnem egy Arany Spirál
Következtetés
Az Arany Spirál egy érdekes téma – amit nem csak a kellemes minták miatt érdemes követni, hanem a mögöttük álló érdekes matematika miatt is.
Remélem, ez segít megválaszolni a kérdésedet, Pehr!