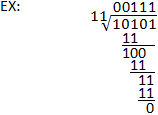Gebruik de volgende rekenmachines om twee binaire waarden bij elkaar op te tellen, van elkaar af te trekken, te vermenigvuldigen of te delen, en om binaire waarden om te zetten in decimale waarden en vice versa.

Binaire berekeningen – optellen, aftrekken, vermenigvuldigen, of delen
Binaire waarde omrekenen naar decimale waarde
Decimale waarde omrekenen naar binaire waarde
Gerelateerde Hex Calculator | IP Subnet Calculator
Het binaire stelsel is een numeriek systeem dat vrijwel identiek functioneert aan het decimale getallensysteem waarmee mensen waarschijnlijk meer vertrouwd zijn. Terwijl het decimale getallensysteem het getal 10 als basis gebruikt, gebruikt het binaire systeem 2. Bovendien worden in het decimale stelsel de cijfers 0 tot en met 9 gebruikt, terwijl in het binaire stelsel alleen 0 en 1 worden gebruikt, en elk cijfer een bit wordt genoemd. Afgezien van deze verschillen worden bewerkingen zoals optellen, aftrekken, vermenigvuldigen en delen volgens dezelfde regels berekend als in het decimale stelsel.
Bijna alle moderne technologie en computers gebruiken het binaire systeem vanwege het gemak waarmee het kan worden geïmplementeerd in digitale schakelingen met behulp van logische poorten. Het is veel eenvoudiger om hardware te ontwerpen die slechts twee toestanden hoeft te detecteren, aan en uit (of waar/onwaar, aanwezig/afwezig, enz.). Het gebruik van een decimaal systeem zou hardware vereisen die 10 toestanden voor de cijfers 0 tot en met 9 kan detecteren, en is gecompliceerder.
Hieronder staan enkele typische omzettingen tussen binaire en decimale waarden:
Binaire/Decimale omzetting
| Decimaal | Binair |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 7 | 111 |
| 8 | 1000 |
| 10 | 1010 |
| 16 | 10000 |
| 20 | 10100 |
Hoewel het werken met binair aanvankelijk verwarrend kan lijken, maar begrijpen dat elke binaire plaatswaarde 2n voorstelt, net zoals elke decimale plaatswaarde 10n voorstelt, zou moeten helpen verduidelijken. Neem bijvoorbeeld het getal 8. In het decimale getallensysteem staat 8 op de eerste decimale plaats links van de decimale punt, wat staat voor de plaats 100. In wezen betekent dit:
8 × 100 = 8 × 1 = 8
Gebruikt men ter vergelijking het getal 18:
(1 × 101) + (8 × 100) = 10 + 8 = 18
In binair wordt 8 voorgesteld als 1000. Van rechts naar links lezend stelt de eerste 0 20 voor, de tweede 21, de derde 22 en de vierde 23; net als in het decimale stelsel, maar dan met een basis van 2 in plaats van 10. Aangezien 23 = 8, wordt op die plaats een 1 ingevuld, wat 1000 oplevert. Met 18, of 10010 als voorbeeld:
18 = 16 + 2 = 24 + 21
10010 = (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (0 × 20) = 18
Het stap-voor-stap-proces om van het decimale naar het binaire stelsel om te zetten is als volgt:
- Vind de grootste macht van 2 die binnen het gegeven getal ligt
- Trek die waarde van het gegeven getal af
- Vind de grootste macht van 2 binnen de in stap 2 gevonden rest
- Herhaal dit totdat er geen rest meer is
- Voeg een 1 in voor elke binaire plaatswaarde die gevonden werd, en een 0 voor de rest
Met het doel van 18 weer als voorbeeld, hieronder een andere manier om dit te visualiseren:
| 2n | 24 | 23 | 22 | 21 | 20 |
| Stoffen binnen 18 | 1 | 0 | 0 | 1 | 0 |
| Target: 18 | 18 – 16 = 2 | → | 2 – 2 = 0 | ||
Het omrekenen van het binaire naar het decimale stelsel is eenvoudiger. Bepaal alle plaatswaarden waar 1 voorkomt, en vind de som van de waarden.
EX: 10111 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 23
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 1 | |
| 16 | 0 | 4 | 2 | 1 |
Hieruit volgt: 16 + 4 + 2 + 1 = 23.
Binaire optelling
Binaire optelling volgt dezelfde regels als optelling in het decimale stelsel, behalve dat in plaats van een 1 over te dragen wanneer de opgetelde waarden gelijk zijn aan 10, overdracht optreedt wanneer het resultaat van optelling gelijk is aan 2. Zie het onderstaande voorbeeld ter verduidelijking.
Merk op dat in het binaire stelsel:
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, de 1 overdragen, d.w.z. 10
EX:
| 10 | 11 | 11 | 10 | 1 | ||
| + | 1 | 0 | 1 | 1 | 1 | |
| = | 1 | 0 | 0 | 1 | 0 | 0 |
Het enige echte verschil tussen binair en decimaal optellen is dat de waarde 2 in het binaire stelsel het equivalent is van 10 in het decimale stelsel. Merk op dat de 1’s in superscript cijfers zijn die worden overgedragen. Een veel voorkomende fout bij het binair optellen is het geval waarin 1 + 1 = 0 ook een 1 heeft die uit de vorige kolom naar rechts is getransporteerd. De waarde onderaan moet dan 1 zijn van de overgeboekte 1 in plaats van 0. Dit kan worden waargenomen in de derde kolom van rechts in het bovenstaande voorbeeld.
Binaire aftrekking
Gelijk aan binaire optelling is er weinig verschil tussen binaire en decimale aftrekking, behalve die welke voortvloeien uit het gebruik van alleen de cijfers 0 en 1. Aftrekken treedt op in elk geval waarin het getal dat wordt afgetrokken groter is dan het getal waarvan het wordt afgetrokken. Bij binaire aftrekking is lenen alleen nodig wanneer 1 wordt afgetrokken van 0. In dat geval wordt de 0 in de leenkolom in feite “2” (de 0-1 wordt 2-1 = 1) en de 1 in de geleende kolom wordt verminderd met 1. Als de volgende kolom ook 0 is, moet uit elke volgende kolom worden geleend tot een kolom met een waarde van 1 kan worden verminderd tot 0. Zie onderstaand voorbeeld ter verduidelijking.
Merk op dat in het binaire stelsel:
- 0 – 0 = 0
0 – 1 = 1, leen 1, resulterend in -1 overgebracht
1 – 0 = 1
1 – 1 = 0
EX1:
| -11 | 20 | 1 | 1 | 1 | ||
| – | 0 | 1 | 1 | 0 | 1 | |
| = | 0 | 1 | 0 | 0 | ||
EX2:
| -11 | 2-10 | 0 | ||
| – | 0 | 1 | 1 | |
| = | 0 | 0 | 1 | |
Merk op dat de weergegeven superscripts de veranderingen zijn die optreden in elk bit bij het lenen. De leenkolom krijgt in wezen 2 door het lenen, en de kolom waarvan geleend wordt, wordt met 1 verminderd.
Binaire vermenigvuldiging
Binaire vermenigvuldiging is aantoonbaar eenvoudiger dan zijn decimale tegenhanger. Aangezien de enige gebruikte waarden 0 en 1 zijn, zijn de resultaten die moeten worden opgeteld ofwel gelijk aan de eerste term, ofwel 0. Merk op dat in elke volgende rij plaatsvervangende 0’s moeten worden toegevoegd, en de waarde naar links moet worden verschoven, net als bij decimale vermenigvuldiging. De complexiteit van de binaire vermenigvuldiging komt voort uit de omslachtige binaire optelling, afhankelijk van het aantal bits in elke term. Zie het onderstaande voorbeeld ter verduidelijking.
Merk op dat in het binaire stelsel:
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
EX:
| 1 | 0 | 1 | 1 | 1 | |||
| × | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | 0 | |
| = | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
Zoals in bovenstaand voorbeeld te zien is, is het proces van binaire vermenigvuldiging hetzelfde als dat van decimale vermenigvuldiging. Merk op dat de 0 plaatshouder op de tweede regel staat. Gewoonlijk is de 0 plaatshouder niet visueel aanwezig in decimale vermenigvuldiging. Hoewel hetzelfde kan worden gedaan in dit voorbeeld (waarbij de 0 plaatshouder wordt verondersteld in plaats van expliciet), is het opgenomen in dit voorbeeld omdat de 0 relevant is voor elke binaire optel / aftrek calculator, zoals degene die op deze pagina. Zonder de 0 zou het mogelijk zijn de fout te maken de 0 uit te sluiten bij het optellen van de hierboven getoonde binaire waarden. Merk nogmaals op dat in het binaire stelsel elke 0 rechts van een 1 relevant is, terwijl elke 0 links van de laatste 1 in de waarde dat niet is.
EX:
- 1 0 1 1 0 0
= 0 0 1 0 1 1 0 0
≠ 1 0 1 0 1 0 0 0
Binaire deling
Het proces van binaire deling is vergelijkbaar met lange deling in het decimale stelsel. Het deeltal wordt nog steeds op dezelfde manier door de deler gedeeld, met als enige belangrijke verschil het gebruik van binaire aftrekking in plaats van decimale aftrekking. Merk op dat een goed begrip van binaire aftrekking belangrijk is voor het uitvoeren van binaire deling. Raadpleeg het onderstaande voorbeeld en de paragraaf over binaire aftrekking voor meer uitleg.