
Fern
Iată o întrebare recentă de la cititorul Pehr din Suedia:
Bună ziua,
În primul rând, minunat site. Îmi place.
Am studiat secțiunea de coordonate polare în speranța de a-mi extinde cunoștințele despre spirala equiangulară. Instrumentele interactive sunt grozave, deși îmi este greu să deriv soluția matematică exactă de ce funcția rezultată pentru spirala de aur este
r = ae^(b(theta))
Pentru câteva informații despre întrebarea lui Pehr, vedeți:
Coordonate polare, curbe în coordonate polare și spirala echi-angulară
Spiralele sunt comune în natură și i-au inspirat pe matematicieni timp de secole.

Spirala Aloe

Spirala galaxiei NGC 5194
Spirale logaritmice
Spirala de aur despre care întreabă Pehr este un caz special al spiralei logaritmice.
Spiralele logaritmice cresc astfel încât unghiul unei drepte de la centrul spiralei la tangenta la curbă în acel punct este constant. Acesta este motivul pentru care sunt cunoscute și sub numele de spirale „equi-angulare”.
Pentru a vedea ce înseamnă acest lucru, cele 3 unghiuri acute marcate în următoarea imagine a ferigii sunt de aproximativ 80°

Ferigă equi-angulară
În mod normal folosim funcții în coordonate polare atunci când descriem spiralele. În caz contrar, dacă folosim coordonate rectangulare obișnuite, formulele devin foarte complexe.
Formula pentru o spirală logaritmică folosind coordonate polare este:
r = aeθ cot b
unde
r este distanța de la origine (sau „polul”)
a este o constantă
θ este unghiul (în radiani) față de axa orizontală. Așadar, coordonatele unui punct de pe curbă în coordonate polare sunt date de (r, θ).
b este unghiul (în radiani – unghiul „egal”) pe care îl face dreapta din centrul spiralei cu tangenta la spirală. În cazul ferigii de mai sus, b ≈ 1,4 radiani (≈ 80°).
Ca o consecință a modului în care am definit spirala logaritmică, raportul dintre distanțele de la centru la fiecare braț al spiralei dintr-o pereche adiacentă este constant.

Brațele spiralei la un raport constant
Raportul
distanța la primul braț: distanța la al doilea braț
= 29:69
≈ 0.42
Celălalt raport
distanța până la al doilea braț: distanța până la al treilea braț
= 69:154
≈ 0,45
Veziem că rapoartele sunt aproape identice. (Într-o spirală logaritmică reală, ele sunt exact aceleași. Alegerea punctului de plecare pentru ferigă nu este o știință exactă)!
Spirala de aur
Spirala de aur este un caz special al spiralei logaritmice.
Potem scrie spirala logaritmică generală ca o funcție în coordonate polare folosind t după cum urmează:
r(t) = aet cot b
Nota: În mod normal, folosim θ pentru variabila independentă, dar adesea folosim t deoarece ne putem gândi că spirala este trasată în timp. În plus, este mai ușor de scris!
Spirala de aur are proprietatea specială astfel încât pentru fiecare 1/4 de tură (90° sau π/2 în radiani), distanța de la centrul spiralei crește cu raportul de aur φ = 1,6180.
Pentru ca acest lucru să se întâmple, cot b trebuie să ia valoarea (care provine din rezolvarea funcției noastre):
![]()
Utilizând această valoare și luând cazul simplu în care a = 1, funcția noastră devine:
![]()
:
r(t) = e0.30635t
De aici încolo vom folosi excelentul instrument grafic gratuit GeoGebra.
Configurarea spiralei de aur folosind GeoGebra
Acum, dacă reprezentăm grafic funcția noastră pe axe de coordonate dreptunghiulare obișnuite în GeoGebra, obținem următoarea curbă exponențială. Observați că r crește cu o rată tot mai mare (devine mai abruptă) pe măsură ce t crește.
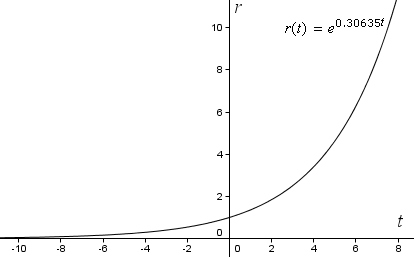
Dar pentru a vedea o spirală, trebuie să reprezentăm grafic curba folosind coordonate polare.
Pentru a converti forma polară (pe care o avem) în formă dreptunghiulară (de care avem nevoie pentru grafic) în Geogebra, trebuie să configurăm și să reprezentăm grafic următoarea funcție:
a(t) = (r(t) cos(t), r(t) sin(t))
Să înlocuim câteva valori importante pentru a vedea ce înseamnă această expresie. Pornind de la t = 0, obținem punctul de plecare al curbei:
a(0) = (r(0) cos(0), r(0) sin(0))
= (1×1, 1×0)
= (1, 0)
Deci înseamnă că pornim de la 1 unitate de la origine de-a lungul axei x pozitive. Puteți vedea punctul de plecare în următorul grafic al spiralei.
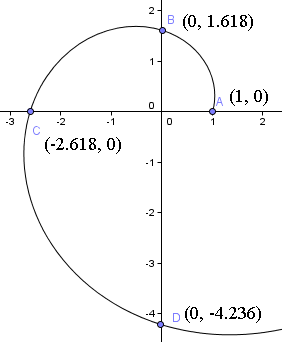
În continuare, ne rotim un sfert de tură și găsim la t = π/2,
a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2))
= (1,618×0, 1,618×1)
= (0, 1,618)
Rețineți că acum ne aflăm la 1,618 unități de la origine pe axa y. Adică, φ = de 1,6180 ori distanța de la care am pornit.
O altă rotație de un sfert de rotație ne aduce la t = π, unde:
a(π) = (r(π) cos(π), r(π) sin(π))
= (-2,618×1, -2,618×0)
= (-2,618, 0)
Ne aflăm acum la 2,618 unități distanță de origine de-a lungul axei x negative, sau φ = 1,6180 ori distanța față de origine la care ne aflam la ultimul sfert de rotație.
Nota:
φ2 = 2,6180
Am putea calcula următoarea noastră poziție, de-a lungul axei y negative, doar înmulțind această ultimă valoare cu φ = 1,6180, obținând:
φ3 = 4,23606…
Așa că spirala va tăia axa y la (0, -4,236).
Încă un sfert de rotație ne va aduce la φ4 = 6,85410… unități de-a lungul axei y pozitive, adică (6,854, 0).
Potem vedea că aceste valori sunt corecte pe graficul spiralei noastre de mai sus.
Dacă vom continua, vom obține o spirală după cum urmează (aceasta este de 2 rotații complete, sau 4π = 720°):
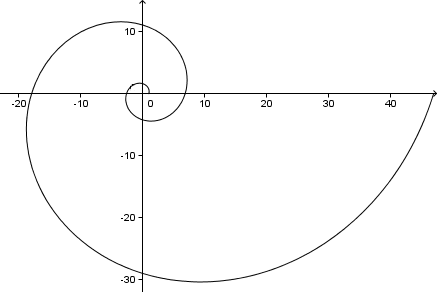
Ca o paranteză, deoarece în această problemă
cot b = 0.30635
atunci
b = arccot 0,30635 = 1,274 radiani sau aproximativ 73°
Acesta este unghiul pe care brațele spiralei noastre îl fac cu o linie din centrul spiralei. Puteți vedea pe graficul de mai sus că fiecare braț al spiralei face un unghi de 73° cu axa x (și cu axa y, sau cu orice linie de la centru).
Aproximarea Spiralei de Aur folosind arce de cerc
Potem obține o spirală care arată destul de asemănător cu Spirala de Aur folosind arce de cerc care cresc în mărime cu Raportul de Aur, după cum urmează.
Începem cu un pătrat 1×1 și trasăm un arc, centru C, prin 2 colțuri astfel încât laturile pătratului să fie tangente la arc (adică să se atingă o singură dată).
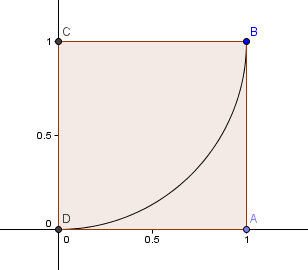
În continuare, plasăm un pătrat cu lungimea laturii φ = 1.6180 deasupra primului nostru pătrat și construim un alt arc de cerc, cu centrul E, ca mai înainte:
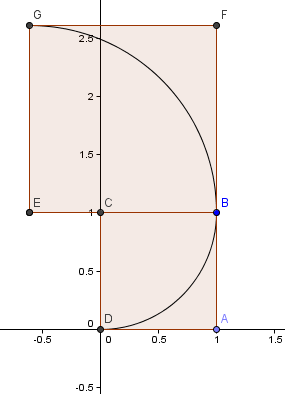
Postăm următorul nostru pătrat la stânga și are laturile φ2 = 2.6180 = 1 + φ.
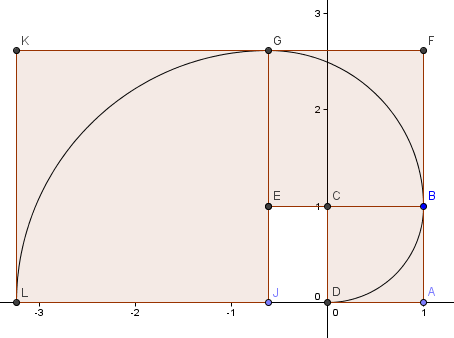
Continuăm modelul (am mai făcut o tură completă) și obținem o spirală care seamănă destul de mult cu Spirala de Aur de mai înainte.
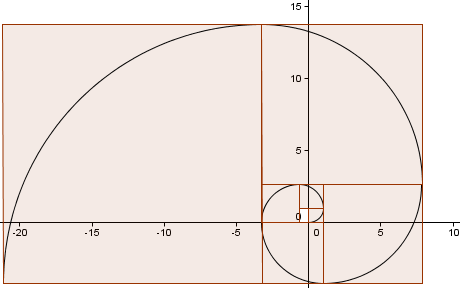
Cât de aproape este aproximația noastră?
Articolul Wikipedia despre Spirala de Aur are o imagine care susține că spirala de mai sus și Spirala de Aur sunt foarte apropiate ca formă.
Iată acea imagine:
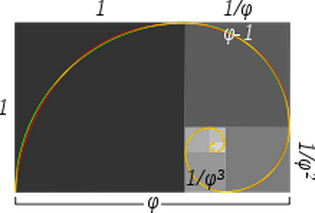
Legenda imaginii afirmă:
Spirale de aur aproximative și adevărate: spirala verde este făcută din sferturi de cercuri tangente la interiorul fiecărui pătrat, în timp ce spirala roșie este o spirală de aur, un tip special de spirală logaritmică. Porțiunile care se suprapun apar în galben. Lungimea laturii unui pătrat mai mare până la următorul pătrat mai mic se află în raportul de aur.
Se poate re-crea acest lucru ?
În imaginea de mai jos, curba roșie este prima parte a spiralei de aur pe care am construit-o mai sus, în timp ce curba verde se bazează pe aproximarea sfertului de tură la care tocmai lucram.
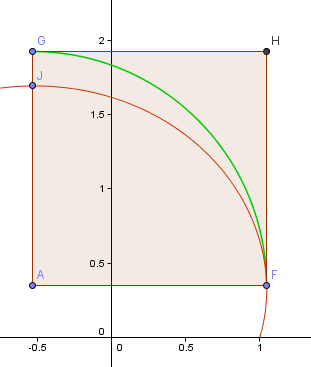
Punctul F este punctul „cel mai drept” de pe spirală, care va fi punctul meu de plecare pentru arcul de sfert de tură. Punctul J este punctul cel mai înalt al acestei porțiuni a spiralei.
Punctul A este intersecția liniilor orizontală și verticală care trec prin F și respectiv J și acesta va fi centrul arcului meu.
Acum, arcul GF nu este deloc aproape de porțiunea aferentă a spiralei FJ.
Să mai facem un pas și să vedem dacă următoarea parte este mai bună.
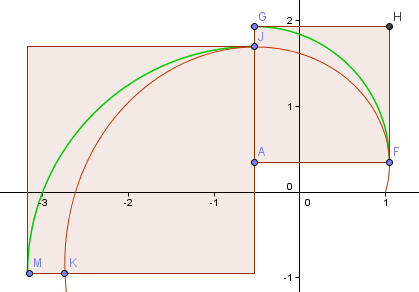
După cum vedeți, este mai rău (așa cum era de așteptat, deoarece ne-am îndepărtat mai mult de origine și brațul spiralei este din ce în ce mai mare).
Evident, acest lucru nu va funcționa niciodată.
Cu toate acestea, în spirala mea anterioară de aur foloseam:
r(t) = e0.30635t
Constanta a, avea valoarea 1.
Dacă vrem ca arcele noastre de aproximare să se potrivească bine cu Spirala de Aur reală, trebuie să folosim o valoare de (probabil nu este surprinzător)
a = φ = 1.618103399..
Aceasta ne dă următoarele curbe, similare cu graficul din Wikipedia.
Curba roșie este Spirala de Aur,
r(t) = 1.618013 e0.30635t
Curba verde este colecția de arce circulare.
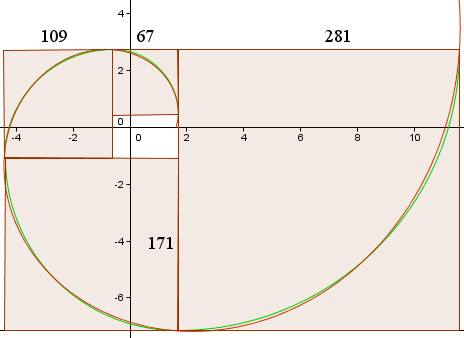
Lungimile laturilor pătratelor (în pixeli) sunt arătate și putem vedea că acestea sunt aproximativ în raportul 1,618013…
Spirala de Aur în media
Din Wolfram’s Mathworld:
În episodul „Masterpiece” (2008) din sezonul 4 al serialului polițist CBS-TV „Criminal Minds”, agenții Unității de analiză comportamentală a FBI se confruntă cu un criminal în serie care folosește secvența numerică Fibonacci pentru a determina numărul de victime pentru fiecare dintre episoadele sale de crimă. În acest episod, personajul Dr. Reid observă, de asemenea, că locațiile crimelor se află pe graficul unei spirale de aur, iar mersul spre centrul spiralei îi permite lui Reid să determine locația bazei de operațiuni a criminalului.
Iată mai multe informații interesante din Wolfram’s Mathworld:
Spirala logaritmică
Pentru tocilari – design folosind Spirala de Aur
Mulți cred că designurile care folosesc Raportul de Aur și Spirala de Aur sunt plăcute la vedere.
Inclusiv Twitter și-a reproiectat recent pagina principală folosind Spirala de Aur.
Iată un articol grozav al unui tip care a contruit o spirală de aur fără imagini. (Mai ales pentru cei interesați de web design)
Spirala de aur fără imagini – folosind CSS și jQuery
După cum sugerează el în articol, trompa unui elefant este, de asemenea, aproape de Spirala de Aur.

Tronc de elefant – aproape o Spirală de Aur
Concluzie
Spirala de Aur este un subiect interesant – unul care merită urmărit nu numai pentru desenele plăcute implicate, ci și pentru matematica interesantă din spatele lor.
Sper că asta ajută la răspunsul la întrebarea ta, Pehr!