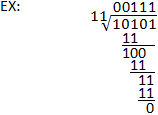Använd följande kalkylatorer för att addera, subtrahera, multiplicera eller dividera två binära värden samt konvertera binära värden till decimalvärden och vice versa.

Binary Calculation-Add, Subtract, Multiply, eller dela
Konvertera binärt värde till decimalvärde
Konvertera decimalvärde till binärt värde
Relaterad Hex-kalkylator | IP-subnäts-kalkylator
Det binära systemet är ett numeriskt system som fungerar i stort sett identiskt med det decimala talsystemet som människor förmodligen är mer bekanta med. Medan det decimala talsystemet använder talet 10 som bas, använder det binära systemet 2. Dessutom, även om decimaltalsystemet använder siffrorna 0 till 9, använder det binära systemet endast 0 och 1, och varje siffra kallas för en bit. Bortsett från dessa skillnader beräknas operationer som addition, subtraktion, multiplikation och division enligt samma regler som i decimalsystemet.
Nästan all modern teknik och datorer använder det binära systemet på grund av att det är lätt att genomföra i digitala kretsar med hjälp av logiska grindar. Det är mycket enklare att konstruera hårdvara som bara behöver upptäcka två tillstånd, på och av (eller sant/falskt, närvarande/frånvarande osv.). Att använda ett decimalsystem skulle kräva hårdvara som kan upptäcka 10 tillstånd för siffrorna 0 till 9, vilket är mer komplicerat.
Nedan följer några typiska konverteringar mellan binära och decimala värden:
Binary/Decimal Conversion
| Decimal | Binary |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 7 | 111 |
| 8 | 1000 |
| 10 | 1010 |
| 16 | 10000 |
| 20 | 10100 |
Om det till en början kan verka förvirrande att arbeta med binära tal, bör förståelsen av att varje binär platsvärde representerar 2n, precis som varje decimalplats representerar 10n, hjälpa till att klargöra. Ta t.ex. talet 8. I det decimala talsystemet är 8 placerat på den första decimalplatsen till vänster om decimalpunkten, vilket betecknar 100-platsen. I huvudsak innebär detta:
8 × 100 = 8 × 1 = 8
Med talet 18 som jämförelse:
(1 × 101) + (8 × 100) = 10 + 8 = 18
I binärt tal representeras 8 som 1000. När man läser från höger till vänster representerar den första 0:an 20, den andra 21, den tredje 22 och den fjärde 23. Precis som i decimalsystemet, fast med basen 2 i stället för 10. Eftersom 23 = 8 anges en 1 i dess position, vilket ger 1000. Med 18 eller 10010 som exempel:
18 = 16 + 2 = 24 + 21
10010 = (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (0 × 20) = 18
Den stegvisa processen för att konvertera från decimalsystemet till det binära systemet är:
- Finn den största potensen av 2 som ligger inom det givna talet
- Subtrahera det värdet från det givna talet
- Finn den största potensen av 2 inom den rest som hittades i steg 2
- Upprepa tills det inte finns någon rest
- Inför en 1 för varje binärt platsvärde som hittades, och en 0 för resten
Om vi återigen använder målet 18 som exempel, kan vi nedan visa ett annat sätt att visualisera detta:
| 2n | 24 | 23 | 22 | 21 | 20 |
| Institutioner inom 18 | 1 | 0 | 0 | 1 | 0 |
| Mål: 18 | 18 – 16 = 2 | → | 2 – 2 = 0 | ||
Konverteringen från det binära till det decimala systemet är enklare. Bestäm alla platsvärden där 1 förekommer och hitta summan av värdena.
EX: 10111 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 23
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 1 | 1 |
| 16 | 0 | 4 | 2 | 1 |
Därmed: 16 + 4 + 2 + 1 = 23.
Binär addition
Binär addition följer samma regler som addition i decimalsystemet förutom att i stället för att föra över en 1 när de adderade värdena är lika med 10, sker överföringen när resultatet av additionen är lika med 2. Se exemplet nedan för ett förtydligande.
Bemärk att i det binära systemet:
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, överför 1, dvs. 10
EX:
| 10 | 11 | 11 | 10 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | ||
| = | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Den enda egentliga skillnaden mellan binär- och decimaladdition är att värdet 2 i binärsystemet motsvarar 10 i decimalsystemet. Observera att de överskrivna 1:orna representerar siffror som överförs. Ett vanligt misstag att se upp för när man utför binär addition är i det fall där 1 + 1 = 0 också har en 1 som förts över från den föregående kolumnen till höger. Värdet längst ner ska då vara 1 från den överförda 1:an i stället för 0. Detta kan observeras i den tredje kolumnen från höger i exemplet ovan.
Binär subtraktion
Som vid binär addition är det inte mycket som skiljer sig mellan binär och decimal subtraktion, förutom de skillnader som uppstår genom att man endast använder siffrorna 0 och 1. Låneberoende uppstår i alla fall där talet som subtraheras är större än talet det subtraheras ifrån. Vid binär subtraktion är det enda fallet där lånande är nödvändigt när 1 subtraheras från 0. När detta inträffar blir 0 i den lånande kolumnen i princip ”2” (0-1 ändras till 2-1 = 1) samtidigt som 1 i den kolumn som lånas från minskas med 1. Om den följande kolumnen också är 0 måste lånande ske från varje efterföljande kolumn tills en kolumn med värdet 1 kan minskas till 0. Se exemplet nedan för att få en förtydligande förklaring.
Bemärk att i det binära systemet:
- 0 – 0 = 0
0 – 1 = 1, låna 1, vilket resulterar i att -1 överförs
1 – 0 = 1
1 – 1 = 0
EX1:
| -11 | 20 | 1 | 1 | 1 | ||
| – | 0 | 1 | 1 | 0 | 1 | |
| = | 0 | 1 | 0 | 1 | 0 | |
EX2:
| -11 | 2-10 | 0 | ||
| – | 0 | 1 | 1 | |
| = | 0 | 0 | 1 | |
Bemärk att de superskript som visas är de förändringar som sker för varje bit vid lån. Den lånande kolumnen får i huvudsak 2 från lånet, och kolumnen som lånas från minskas med 1.
Binär multiplikation
Binär multiplikation är utan tvekan enklare än sin decimala motsvarighet. Eftersom de enda värden som används är 0 och 1 är de resultat som måste adderas antingen samma som den första termen eller 0. Observera att i varje efterföljande rad måste platshållaren 0 läggas till och värdet förskjutas till vänster, precis som vid decimalmultiplikation. Komplexiteten i binär multiplikation beror på en omständlig binär addition som är beroende av hur många bitar som finns i varje term. Se exemplet nedan för ett förtydligande.
Notera att i det binära systemet:
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
EX:
| 1 | 0 | 1 | 1 | 1 | |||
| × | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | 0 | |
| = | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
Som framgår av exemplet ovan, är processen för binär multiplikation densamma som för decimalmultiplikation. Observera att platshållaren 0 är skriven på den andra raden. Typiskt sett är 0-placeringshållaren inte visuellt närvarande vid decimalmultiplikation. Även om samma sak kan göras i det här exemplet (där 0-placeringshållaren antas i stället för att vara explicit) är den inkluderad i det här exemplet eftersom 0 är relevant för alla binära additions-/subtraktionsräknare, som den som tillhandahålls på den här sidan. Utan att 0 visas skulle det vara möjligt att göra misstaget att utesluta 0 när man adderar de binära värden som visas ovan. Observera återigen att i det binära systemet är varje 0 till höger om en 1 relevant, medan varje 0 till vänster om den sista 1:an i värdet inte är det.
EX:
- 1 0 1 0 1 1 0 0 0
= 0 0 1 0 1 0 1 1 0 0 0
≠ 1 0 1 0 1 0 1 0 0 0 0 0 0
Binärdivision
Förfarandet vid binärdivision liknar långdivision i decimalsystemet. Utdelningen divideras fortfarande med divisorn på samma sätt, med den enda betydande skillnaden att binär subtraktion används i stället för decimal subtraktion. Observera att en god förståelse för binär subtraktion är viktig för att genomföra binär division. Se exemplet nedan samt avsnittet om binär subtraktion för förtydligande.