
Fern
Här kommer en fråga från läsaren Pehr i Sverige:
Hej,
Först av allt, underbar webbplats. Älskar den.
Jag har studerat avsnittet om polarkoordinater i hopp om att kunna utöka mina kunskaper om den ekviangulära spiralen. De interaktiva verktygen är fantastiska, men jag har svårt att härleda den exakta matematiska lösningen på varför den resulterande funktionen för den gyllene spiralen är
r = ae^(b(theta))
För lite bakgrund till Pehrs fråga, se:
Polära koordinater, kurvor i polära koordinater och ekviovinkelspiral
Spiraler är vanliga i naturen och har inspirerat matematiker i århundraden.

Aloe spiral

Spiralgalaxen NGC 5194
Logaritmiska spiraler
Den gyllene spiralen som Pehr frågar om är ett specialfall av den logaritmiska spiralen.
Logaritmiska spiraler växer så att vinkeln på en linje från spiralens centrum till tangenten till kurvan i den punkten är konstant. Det är därför de också kallas ”likvinkliga” spiraler.
För att se vad detta innebär kan man se att de tre spetsiga vinklarna som är markerade i följande bild av ormbunken är ungefär 80°

Klikvinklig ormbunke
Vi använder normalt funktioner i polära koordinater när vi beskriver spiraler. Om vi annars använder vanliga rektangulära koordinater blir formlerna mycket komplicerade.
Formeln för en logaritmisk spiral med hjälp av polarkoordinater är:
r = aeθ cot b
där
r är avståndet från origo (eller ”polen”)
a är en konstant
θ är vinkeln (i radianer) från den horisontella axeln. Så koordinaterna för en punkt på kurvan i polarkoordinater ges av (r, θ).
b är den vinkel (i radianer – den ”lika” vinkeln) som linjen från spiralens centrum gör med tangenten till spiralen. I ormbunksfallet ovan är b ≈ 1,4 radianer (≈ 80°).
Som en följd av hur vi definierade den logaritmiska spiralen är förhållandet mellan avstånden från centrum till varje spiralarmen i ett intilliggande par konstant.

Spiralarmar i konstant förhållande
Förhållandet
avstånd till den första armen: avstånd till den andra armen
= 29:69
≈ 0.42
Det andra förhållandet
avstånd till andra armen: avstånd till tredje armen
= 69:154
≈ 0,45
Vi ser att förhållandena är nästan lika. (I en verklig logaritmisk spiral är de exakt lika. Att välja startpunkt för ormbunken är ingen exakt vetenskap!).
Gyllene spiral
Den gyllene spiralen är ett specialfall av den logaritmiska spiralen.
Vi kan skriva den allmänna logaritmiska spiralen som en funktion i polära koordinater med hjälp av t på följande sätt:
r(t) = aet cot b
Notera: Normalt använder vi θ för den oberoende variabeln, men vi använder ofta t eftersom vi kan tänka oss att spiralen spåras ut över tiden. Dessutom är det lättare att skriva!
Den gyllene spiralen har den speciella egenskapen att för varje 1/4 varv (90° eller π/2 i radianer) ökar avståndet från spiralens centrum med det gyllene snittet φ = 1,6180.
För att detta ska inträffa måste cot b anta värdet (vilket kommer från lösningen av vår funktion):
![]()
Med hjälp av detta värde, och med det enkla fallet där a = 1, blir vår funktion:
r(t) = e0.30635t
Vi kommer att använda det utmärkta gratis grafiska verktyget GeoGebra hädanefter.
Sätt upp den gyllene spiralen med hjälp av GeoGebra
Om vi nu graferar vår funktion på vanliga rektangulära koordinataxlar i GeoGebra får vi följande exponentialkurva. Observera att r ökar i allt snabbare takt (den blir brantare) när t ökar.
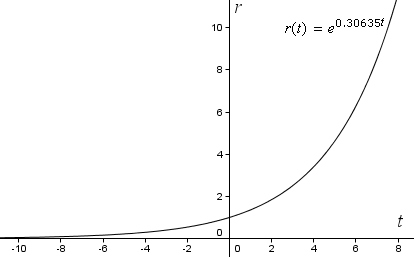
Men för att se en spiral måste vi grafera kurvan med hjälp av polarkoordinater.
För att omvandla polarformen (som vi har) till rektangulär form (som vi behöver för grafen) i Geogebra måste vi ställa upp och grafera följande funktion:
a(t) = (r(t) cos(t), r(t) sin(t))
Låt oss ersätta några viktiga värden för att se vad detta uttryck betyder. Om vi börjar vid t = 0 får vi kurvans utgångspunkt:
a(0) = (r(0) cos(0), r(0) sin(0))
= (1×1, 1×0)
= (1, 0)
Det betyder alltså att vi börjar 1 enhet från origo längs den positiva x-axeln. Du kan se startpunkten i följande graf över spiralen.
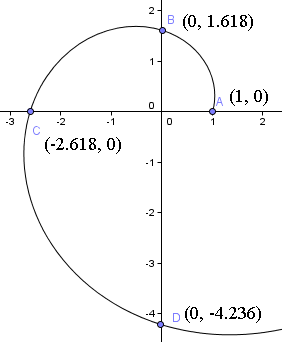
Nästan roterar vi ett kvarts varv och finner vid t = π/2,
a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2)).
= (1,618×0, 1,618×1)
= (0, 1,618)
Bemärk att vi nu är 1,618 enheter från origo uppåt på y-axeln. Det vill säga φ = 1,6180 gånger avståndet vi startade från.
En annan rotation på ett kvarts varv ger oss t = π, där:
a(π) = (r(π) cos(π), r(π) sin(π)).
= (-2,618×1, -2,618×0)
= (-2,618, 0)
Vi är nu 2,618 enheter bort från origo längs den negativa x-axeln, eller φ = 1,6180 gånger avståndet från origo som vi hade vid det senaste kvartsvarvet.
Notera:
φ2 = 2,6180
Vi kan räkna ut vår nästa position, längs den negativa y-axeln, genom att bara multiplicera detta sista värde med φ = 1,6180, vilket ger oss:
φ3 = 4,23606…
Så spiralen kommer att skära y-axeln vid (0, -4,236).
Ett kvartsvarv till ger oss φ4 = 6,85410… enheter längs den positiva y-axeln, det vill säga (6,854, 0).
Vi kan se att dessa värden är korrekta på vår spiralgraf ovan.
Om vi fortsätter får vi en spiral som ser ut på följande sätt (detta är 2 kompletta varv, eller 4π = 720°):
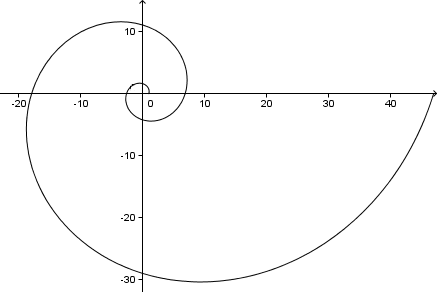
Som ett sidospår, eftersom i detta problem
cot b = 0.30635
då
b = arccot 0,30635 = 1,274 radianer eller cirka 73°
Detta är den vinkel som våra spiralarmar gör med en linje från spiralens centrum. Du kan se på grafen ovan att varje spiralarmen gör en vinkel på 73° med x-axeln (och y-axeln, eller vilken linje som helst från centrum).
Närma sig den gyllene spiralen med hjälp av cirkelbågar
Vi kan få fram en spiral som ser ganska likadan ut som den gyllene spiralen genom att använda cirkelbågar som ökar i storlek med det gyllene snittet, enligt följande.
Vi börjar med en kvadrat 1×1 och ritar en båge, centrum C, genom 2 hörn så att sidorna i kvadraten tangerar bågen (det vill säga de berörs bara en gång).
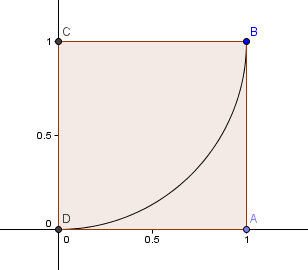
Nästan placerar vi en kvadrat med sidlängden φ = 1.6180 ovanför vår första kvadrat och konstruerar ytterligare en cirkelbåge, centrum E, som tidigare:
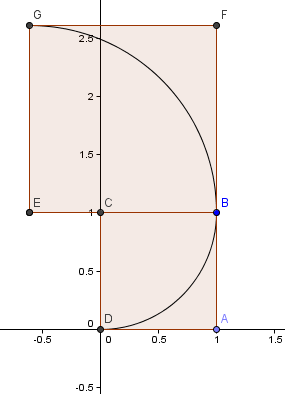
Vår nästa kvadrat går till vänster och har sidorna φ2 = 2,6180 = 1 + φ.
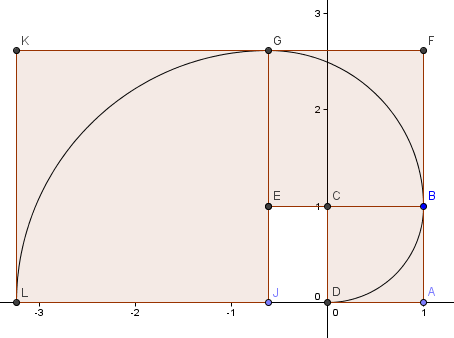
Vi fortsätter mönstret (vi har gått ytterligare ett helt varv) och får en spiral som ser ganska mycket ut som vår gyllene spiral från tidigare.
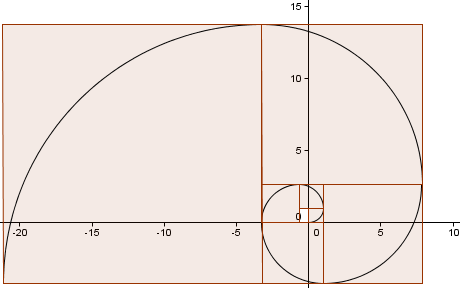
Hur nära är vår approximation?
Wikipedias artikel om den gyllene spiralen har en bild som påstår att ovanstående spiral och den gyllene spiralen ligger mycket nära varandra i form.
Här är den bilden:
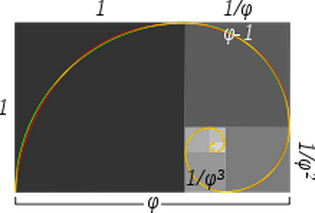
I bildtexten till bilden står det:
Närliggande och äkta gyllene spiraler: den gröna spiralen består av kvartscirklar som tangerar insidan av varje kvadrat, medan den röda spiralen är en gyllene spiral, en speciell typ av logaritmisk spiral. Överlappande delar visas gula. Längden mellan sidan av en större kvadrat och nästa mindre kvadrat är i gyllene snittet.
Kan vi återskapa detta?
I bilden nedan är den röda kurvan den första delen av den gyllene spiralen som vi konstruerade ovan, medan den gröna kurvan är baserad på den approximation av kvartssvängningen som vi just arbetade med.
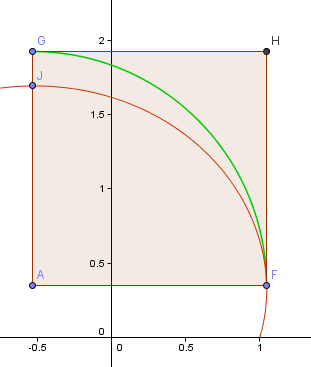
Punkten F är den ”högraste” punkten på spiralen, vilket kommer att bli min utgångspunkt för kvartssvängningsbågen. Punkten J är den högsta punkten på denna del av spiralen.
Punkten A är skärningspunkten mellan de horisontella och vertikala linjerna som går genom F respektive J och detta kommer att bli mittpunkten för min båge.
Nu ligger bågen GF inte alls nära den relaterade delen av spiralen FJ.
Vi gör ett steg till och ser om nästa del är bättre.
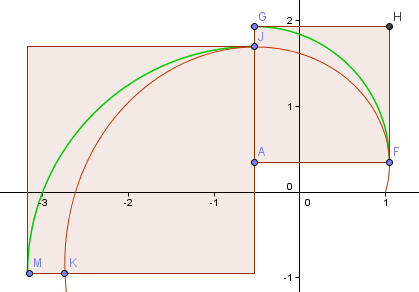
Som ni ser är det sämre (som väntat, eftersom vi har rört oss längre bort från ursprunget och spiralarmen blir större).
Det är uppenbart att detta aldrig kommer att fungera.
I min tidigare gyllene spiral använde jag dock:
r(t) = e0.30635t
Konstanten a hade värdet 1.
Om vi vill att våra approximativa bågar ska passa bra till den verkliga gyllene spiralen måste vi använda ett värde på (förmodligen inte överraskande)
a = φ = 1,618103399…
Detta ger oss följande kurvor, som liknar grafen i Wikipedia.
Den röda kurvan är den gyllene spiralen,
r(t) = 1,618013 e0,30635t
Den gröna kurvan är samlingen av cirkelbågar.
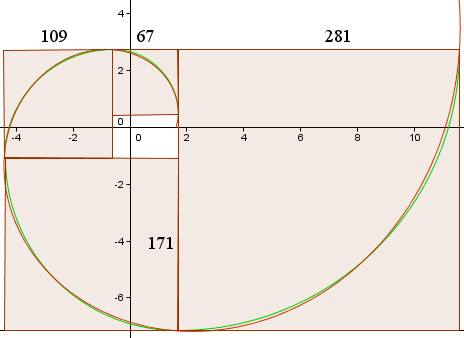
Fältets sidlängd (i pixlar) visas och vi kan se att de är ungefär i förhållandet 1,618013…
Den gyllene spiralen i media
Från Wolfram’s Mathworld:
I avsnittet ”Masterpiece” (2008) i säsong 4 av CBS:s kriminaldrama ”Criminal Minds” konfronteras agenterna från FBI:s enhet för beteendeanalys med en seriemördare som använder Fibonacci-nummerserien för att bestämma antalet offer för var och en av sina mordepisoder. I det här avsnittet märker karaktären Dr. Reid också att platserna för morden ligger på grafen för en gyllene spiral, och genom att gå till mitten av spiralen kan Reid bestämma platsen för mördarens operationsbas.
Här finns mer intressant information från Wolfram’s Mathworld:
Logaritmisk spiral
För nördarna – design med hjälp av den gyllene spiralen
Flera människor anser att design med hjälp av det gyllene snittet och den gyllene spiralen är en fröjd för ögat.
Även Twitter har nyligen omdesignat sin huvudsida med hjälp av den gyllene spiralen.
Här finns en bra artikel av en kille som har konstruerat en gyllene spiral utan bilder. (Mest för dem som är intresserade av webbdesign)
Gyllene spiral utan bilder – med hjälp av CSS och jQuery
Som han antyder i artikeln ligger en elefants snabel också nära den gyllene spiralen.

Elefantstam – nästan en gyllene spiral
Slutsats
Den gyllene spiralen är ett intressant ämne – ett ämne som är värt att följa upp, inte bara för de trevliga konstruktioner som ingår, utan också för den intressanta matematiken bakom dem.
Jag hoppas att detta hjälper till att besvara din fråga, Pehr!