Free Press

Násobení matic

Existují přesně dva způsoby násobení matic. Prvním způsobem je násobení matice skalárem. Tento postup se nazývá skalární násobení. Druhým způsobem je násobení matice jinou maticí. To je známé jako násobení matic.

Skalární násobení

Skalární násobení je vlastně velmi jednoduchá maticová operace. Chceme-li vynásobit skalár s maticí, jednoduše vezmeme skalár a vynásobíme ho s každým zápisem v matici. Udělejme si příklad:

Otázka 1: Vypočítejte 2A2A2A, jestliže

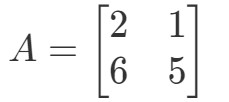
V otázce se po nás chce, abychom zjistili, co je 2A2A2A. Jinými slovy zjišťujeme

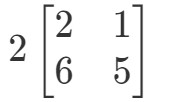
Všimněte si, že máme-li ke každému zápisu v matici násobit 2, dostaneme, že:

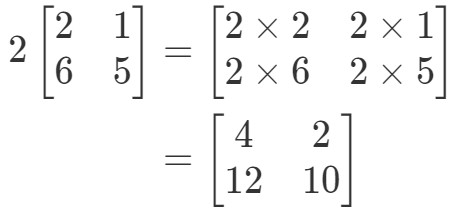
Velmi jednoduché! Uděláme další.

Úloha 2: Vypočítejte 0A0A0A, jestliže

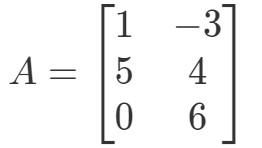
Znovu se snažíme najít 0A0A0A. To znamená, že budeme hledat odpověď na

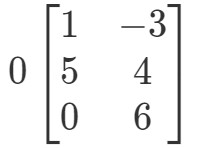
Matice bude mít zvláštní tvar, ale koncept zůstává stejný. Ke každému zápisu v matici budeme stále násobit skalár 0. Tím získáme:

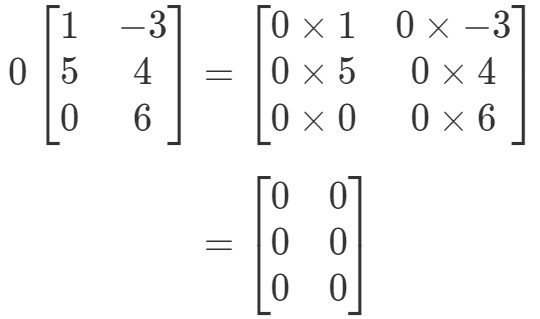
Všimněte si, že všechny záznamy v matici jsou 0. Taková matice se nazývá nulová matice, která má rozměry 3 x 2.

Když už jsme se dobře seznámili se skalárním násobením, proč nepřejít k násobení matic?

Jak násobit matice

Chceme-li násobit matici jinou maticí, musíme se nejprve dozvědět, co je to bodový součin.

Co je to bodový součin?

Bodový součin (známý také jako násobení vektorů) je způsob výpočtu součinu dvou vektorů. Nechť jsou to například tyto dva vektory:

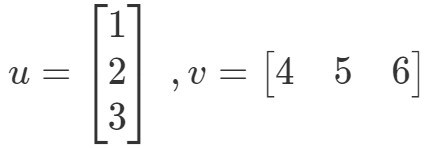
Jak bych tyto dva vektory vynásobil? Jednoduše stačí vynásobit příslušné položky a součin sečíst. Jinými slovy,

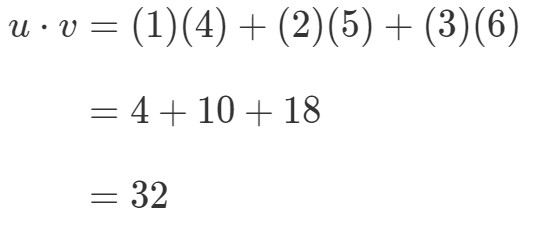
Takto získáme vynásobením vektorů jedinou hodnotu. Všimněte si však, jak to, že oba vektory mají stejný počet zápisů. co když má jeden z vektorů jiný počet zápisů než druhý? Například nechť

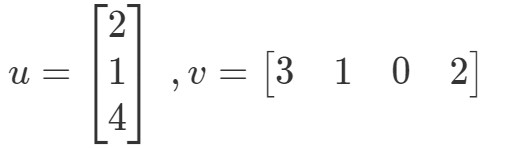
Pokud bych příslušné položky vynásobil a sečetl je všechny dohromady, pak dostanu:

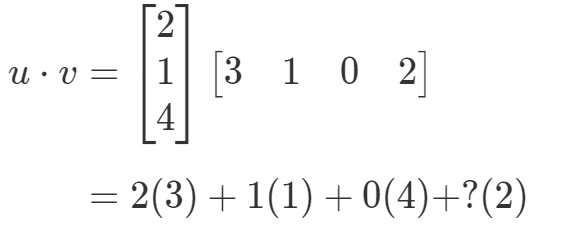
Tady je problém. První tři položky mají odpovídající položky, kterými se násobí, ale poslední položka ne. Co zde tedy uděláme? Odpověď zní, že zde nemůžeme dělat nic. Znamená to pouze, že nemůžeme vypočítat tečkový součin těchto dvou vektorů.

Takže závěrem, nemůžeme najít tečkový součin dvou vektorů, které mají různé počty zápisů. Musí mít stejný počet zápisů.

2 x 2 násobení matic

Takže jaký smysl mělo učit se tečkový součin? No, bodový součin budeme používat, když budeme násobit dvě matice dohromady. Při násobení matice jinou maticí chceme s řádky a sloupci zacházet jako s vektorem. Přesněji řečeno, s každým řádkem první matice chceme zacházet jako s vektory a s každým sloupcem druhé matice jako s vektory. Udělejme si příklad.

Úloha 3: Najděte A∙BA \bullet BA∙B jestliže

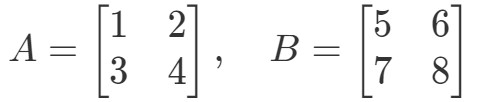
Násobením obou matic získáme:

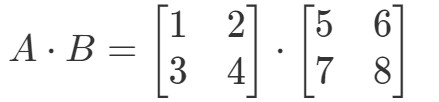
Nyní řádky a sloupce, na které se zaměřujeme, jsou

kde r1r_{1}r1 je první řádek, r2r_{2}r2 je druhý řádek a, c1,c2c_{1}, c_{2}c1,c2 jsou první a druhý sloupec. Nyní budeme s každým řádkem a sloupcem, které zde vidíme, zacházet jako s vektorem.

Všimněte si, že vynásobením matice 2 x 2 s jinou maticí 2 x 2 získáme matici 2 x 2. Všimněte si, že matice 2 x 2 se vynásobí s jinou maticí 2 x 2. Jinými slovy, matice, kterou dostaneme, by měla mít 4 položky.

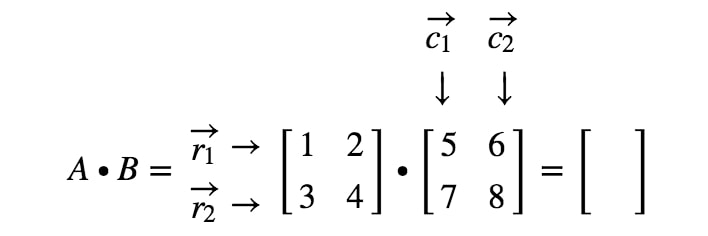
Jak přesně získáme první položku? No, všimněte si, že první položka se nachází na prvním řádku a v prvním sloupci. Takže jednoduše vezmeme tečkový součin r1r_{1}r1 a c1c_{1}c1. První zadání tedy bude

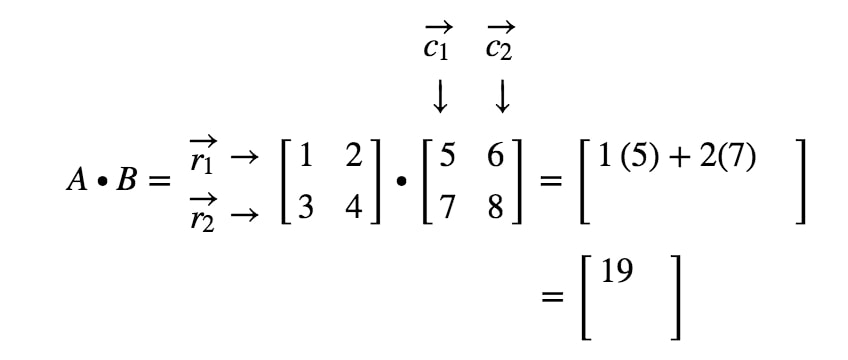
Jak tentokrát získáme druhé zadání? No, všimněte si, že umístění druhého zápisu je v prvním řádku a druhém sloupci. Jednoduše tedy vezmeme tečkový součin r1r_{1}r1 a c2c_{2}c2. Druhý zápis tedy bude

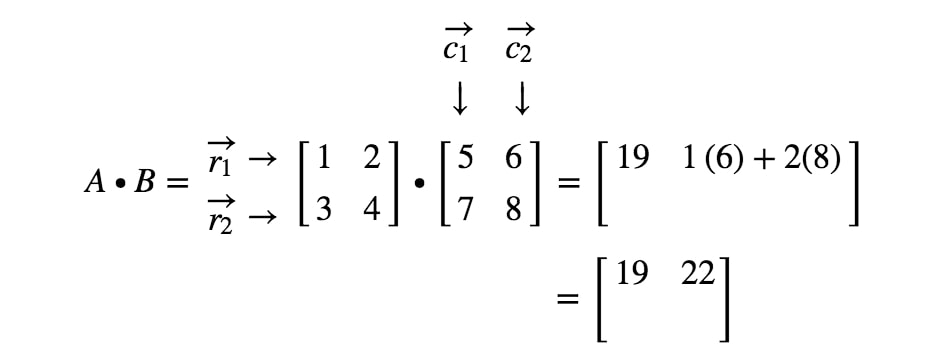
Nyní použijeme stejnou strategii při hledání posledních dvou zápisů. Všimněte si, že předposlední zápis se nachází ve 2.2^{druhém}2. řádku a 1.1^{st}1. sloupci a poslední zápis se nachází ve 2.2^{druhém}2. řádku a 2.2^{druhém}2. sloupci. Vezmeme tedy bodový součin r2r_{2}r2 a c1c_{1}c1 a bodový součin r2r_{2}r2 a c2c_{2}c2. Tím získáme:

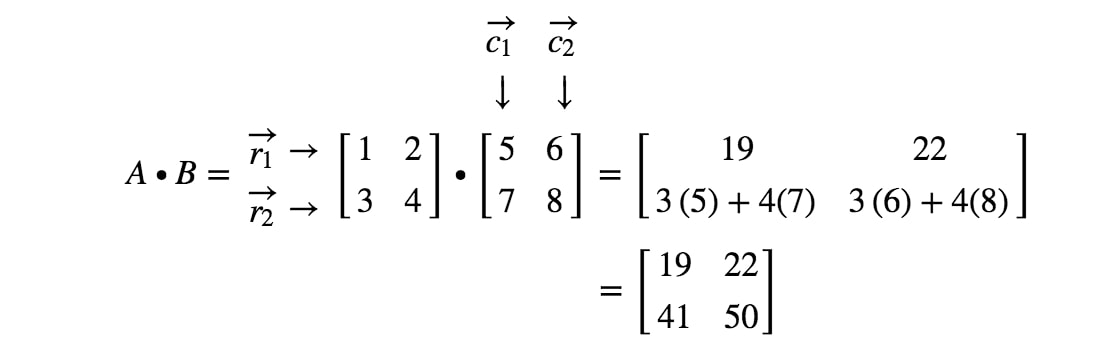
Nyní máme hotovo! Toto dostaneme, když násobíme matice 2 x 2. Obecně platí, že vzorec pro násobení matic 2 x 2 je

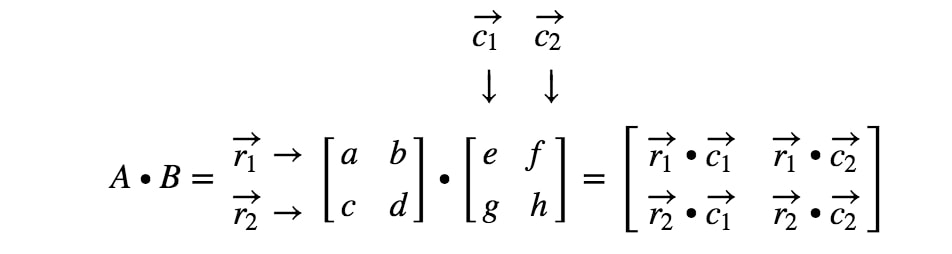
Násobení matic 3 x 3

Nyní je postup násobení matic 3 x 3 velmi podobný postupu násobení matic 2 x 2. V případě, že se jedná o násobení matic 2 x 2, můžeme použít vzorce pro násobení matic 3 x 3. Proč si opět neuděláme příklad na násobení matic

Otázka 4:Najděte A∙BA \bullet BA∙B if

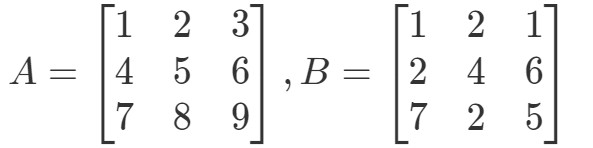
Nejprve si všimněte, že jejich vynásobením bychom měli získat další matici 3 x 3. Všimněte si, že násobení matic 3 x 2 a 3 by se mělo odehrávat v rámci jedné matice. Jinými slovy,

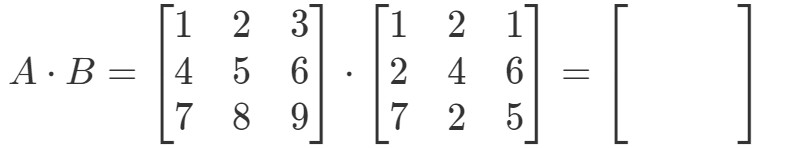
Nyní si označíme všechny řádky první matice a sloupce druhé matice.

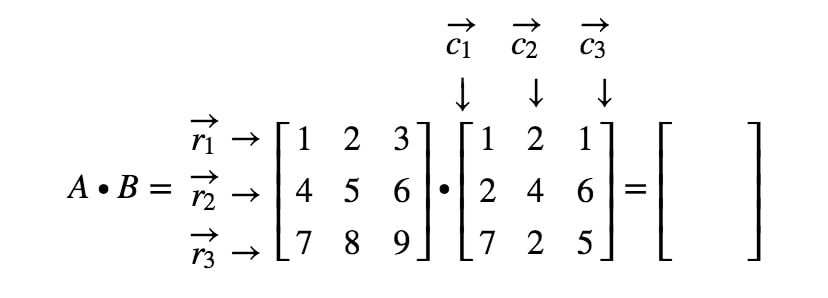
Všimněte si, že první položka matice se nachází v 1.1^{st}1. řádku a 1.1^{st}1. sloupci, takže vezmeme bodový součin r1r_{1}r1 a c1c_{1}c1. Tím získáme:

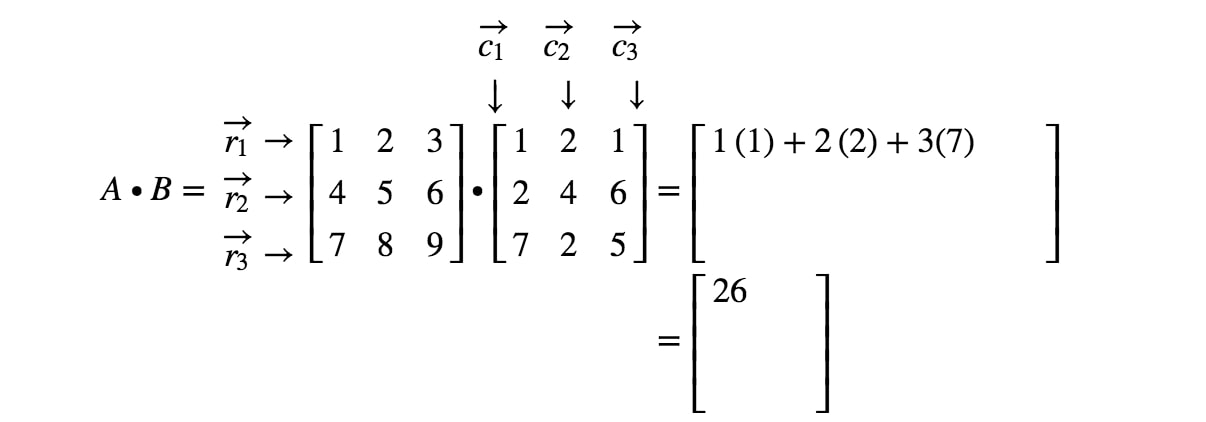
Nyní si všimněte, že druhý zápis matice se nachází v 1.1^{st}1. řádku a 2.2^{nd}2. sloupci. Vezmeme tedy tečkový součin r1r_{1}r1 a c2c_{2}c2. Tím získáme:

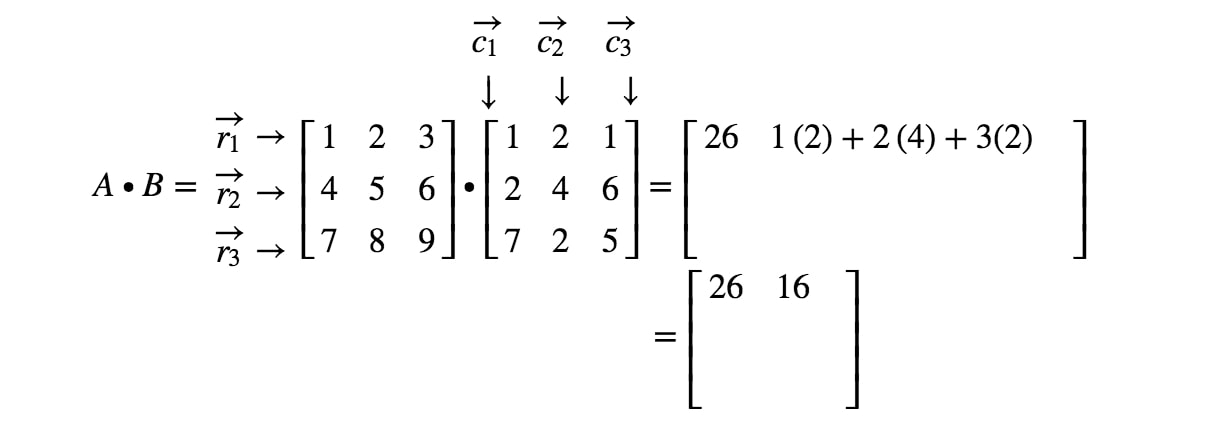
Pokud máme nadále lokalizovat všechny položky a provést bodový součin odpovídající řádkům a sloupcům, pak dostaneme konečný výsledek:

Máme hotovo! Všimněte si, že čím jsou matice větší, tím je násobení matic zdlouhavější. Je to proto, že musíme pracovat se stále větším počtem čísel! Obecně platí, že vzorec pro násobení matic 3 x 3 je

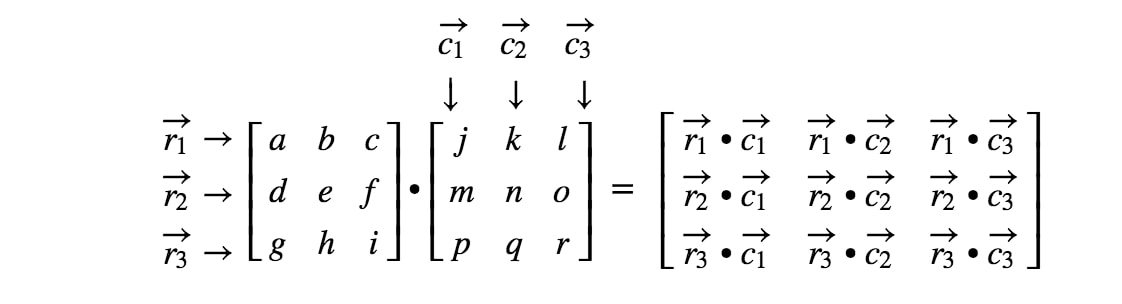
Jak násobit matice s různými rozměry?“

Dosud jsme násobili matice se stejnými rozměry. Dále víme, že vynásobením dvou matic se stejným rozměrem získáme matici stejných rozměrů. Co se však stane, když vynásobíme matici s různými rozměry? Jak bychom zjistili rozměry vypočtené matice? Nejprve se musíme přesvědčit, že vynásobením matic získáme definovanou matici.

Je matice definovaná?“

Existují případy, kdy není možné vynásobit dvě matice dohromady. Pro tyto případy nazýváme matici nedefinovanou. Jak poznáme, že jsou nedefinované?“

Součin dvou matic je definovaný pouze tehdy, je-li počet sloupců první matice roven počtu řádků druhé matice.

Zkusme tuto definici použít v tomto příkladu.

Otázka 5: Nechť

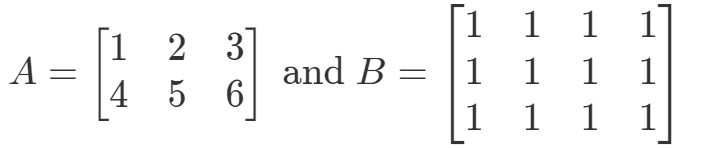
Je definována matice A∙BA \bullet BA∙B?

Nejprve si všimněte, že první matice má 3 sloupce. Také druhá matice má 3 řádky. Protože jsou obě rovny 3, pak vím, že A∙BA \bullet BA∙B je definována.

Když už víme, že je definována, jak bychom poznali rozměry A∙BA \bullet BA∙B?

Vlastnost rozměrů

Chceme-li zjistit rozměry A∙BA \bullet BA∙B, musíme se nejprve podívat na rozměry a zvlášť.

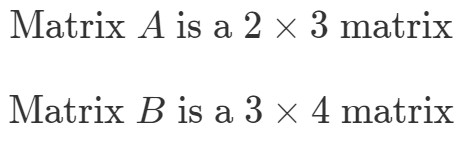
Nyní dáme rozměry matic vedle sebe takto:

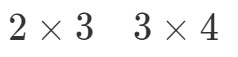
Nyní vezmeme první číslo a poslední číslo a spojíme je, abychom dostali rozměry A∙BA \bullet BA∙B. Vidíme, že první číslo je 2 a poslední číslo je 4. Takže rozměry matice A∙BA \bullet BA∙B budou:

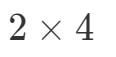
Teď, když známe rozměry matice, můžeme už jen vypočítat jednotlivé položky pomocí bodových součinů. Tím získáme:

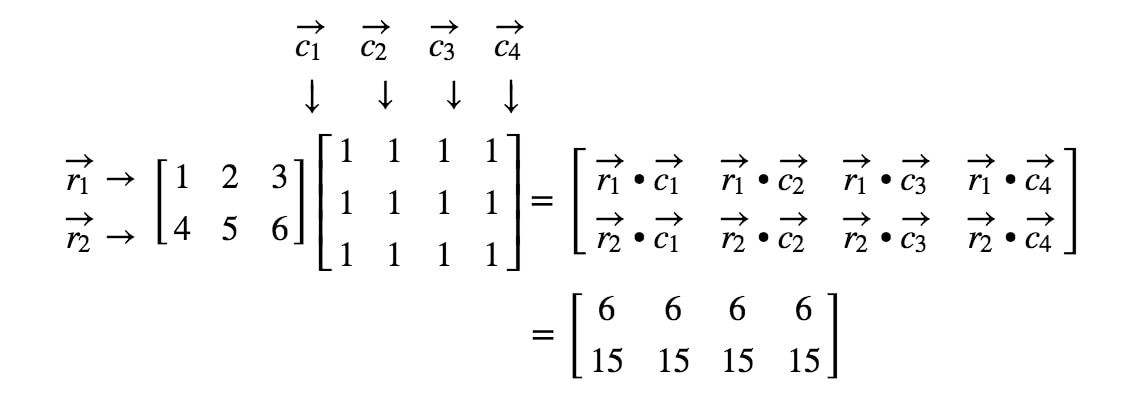
Když už dobře víme, jak násobit matice, proč se nepodívat na některá pravidla násobení matic?

Vlastnosti násobení matic

Takže jaké vlastnosti vlastně násobení matic má? Nejprve si vše formálně definujme.

Nechť X,Y,ZX, Y, ZX,Y,Z jsou matice, InI_{n}In je matice identity a OnO_{n}On je nulová matice. Má-li všech pět těchto matic stejné rozměry, pak budeme mít následující vlastnosti násobení matic na matice:

Asociativní vlastnost říká, že na pořadí, v jakém násobíme, nezáleží. Jinými slovy, výpočet X∙YX \bullet YX∙Y a následné vynásobení ZZZ by dalo stejný výsledek jako výpočet Y∙ZY \bullet ZY∙Z a následné vynásobení XXX. Udělejme si příklad.

Otázka 6: Ukažte, že asociativní vlastnost funguje s těmito maticemi:

Podíváme-li se na levou stranu rovnice v asociativní vlastnosti, vidíme, že (XY)Z(XY)Z(XY)Z dává:

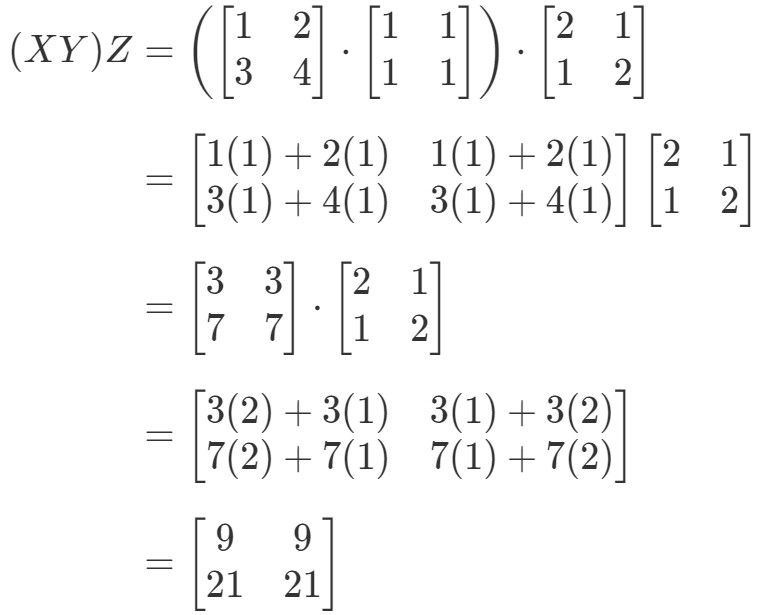
Podíváme-li se nyní na pravou stranu rovnice v asociativní vlastnosti, vidíme, že X(YZ)X(YZ)X(YZ) dává:

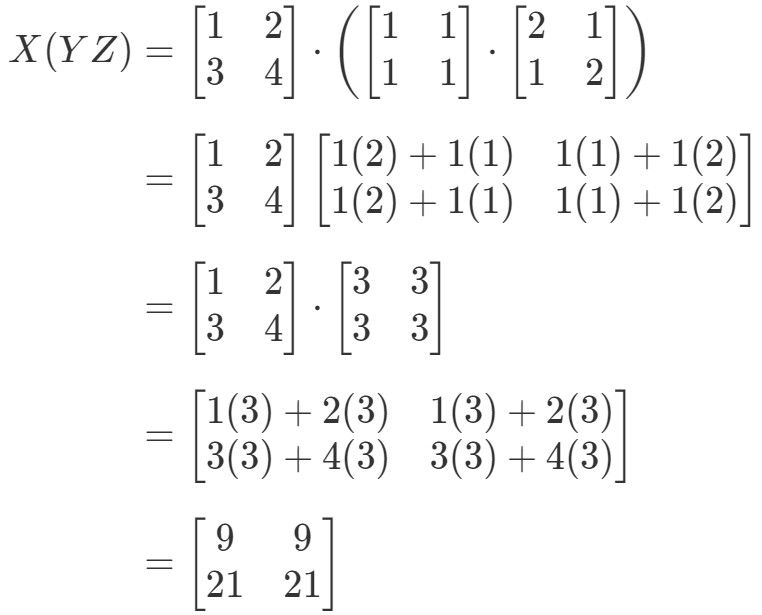
Vidíme, že levá i pravá strana rovnice se rovnají. Víme tedy, že asociativní vlastnost skutečně funguje! Opět to znamená, že na pořadí násobení matic nezáleží!

Další vlastností je vlastnost distributivní. Distributivní vlastnost říká, že:

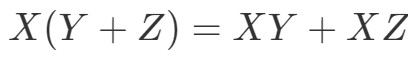
Vidíme, že můžeme použít foliovou techniku i pro matice. Abychom si ukázali, že tato vlastnost funguje, uděláme si příklad:

Úkol 7: Ukažte, že distributivní vlastnost funguje pro následující matice:

Vidíme, že levá strana rovnice je X(Y+Z)X(Y + Z)X(Y+Z). Proto nám výpočet dává:

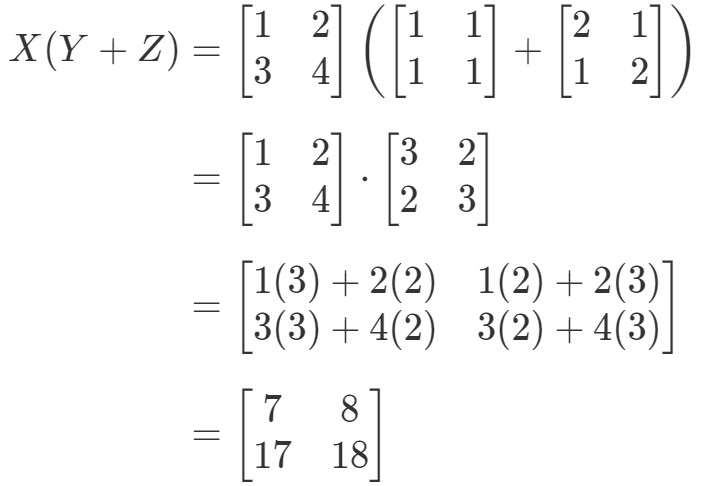
Nyní zkontrolujeme, zda nám pravá strana rovnice dává úplně totéž. Všimněte si, že pravá strana rovnice je XY+XZXY + XZXY+XZ. Výpočet nám dává:

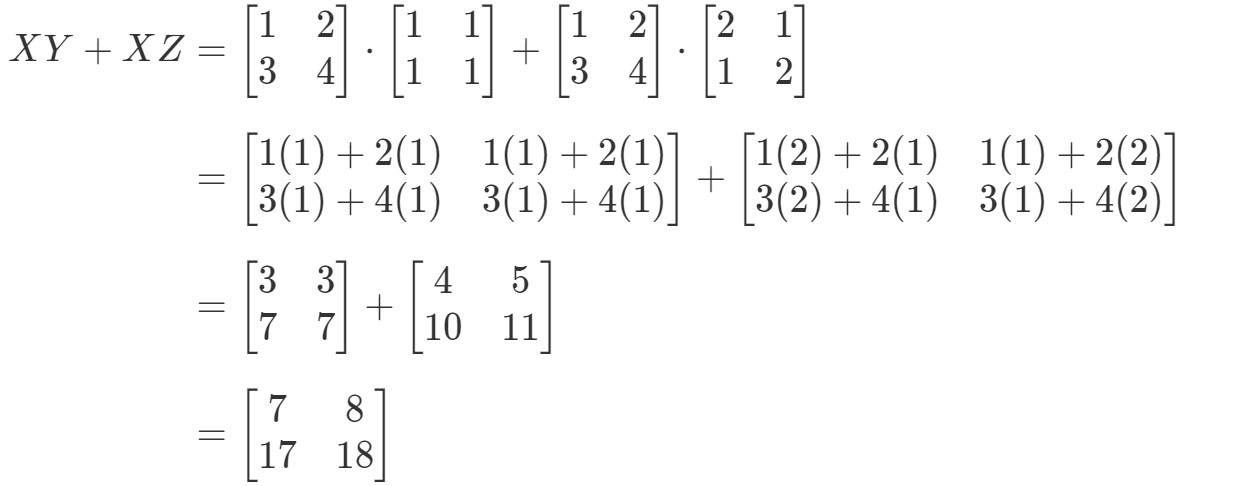
Všimněte si, že levá strana rovnice je přesně stejná jako pravá strana rovnice. Můžeme tedy potvrdit, že distributivní vlastnost skutečně funguje.

Je násobení matic komutativní?

Víme, že násobení matic splňuje asociativní i distributivní vlastnost, o komutativní vlastnosti jsme však vůbec nemluvili. Znamená to, že ji násobení matic nesplňuje? Ve skutečnosti nesplňuje a můžeme si to ověřit na příkladu.

Otázka 8: Je-li násobení matic komutativní, pak musí platit následující:

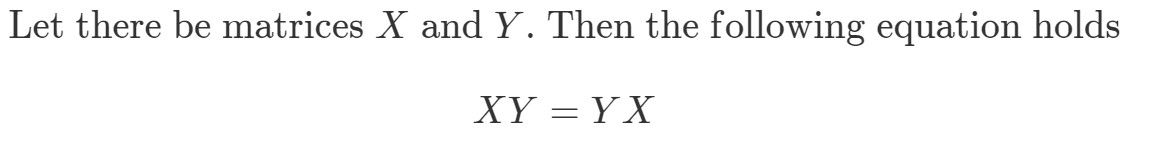
Ukažte, že XYeqYXXY eq YXXYeqYX, jestliže

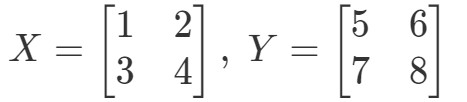
Nejprve vypočítáme levou stranu rovnice. Výpočtem XYXYXY získáme:

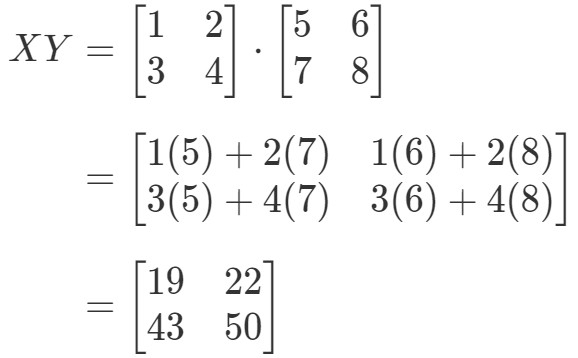
Nyní výpočtem pravé strany rovnice získáme:

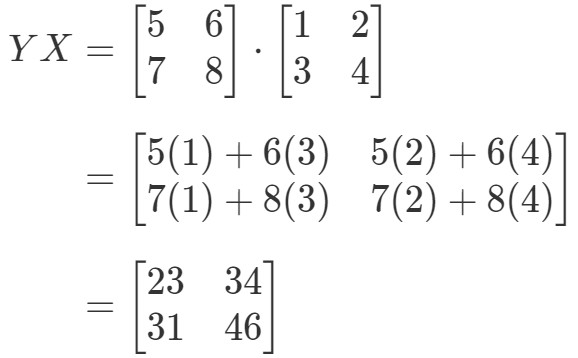
Jak vidíte,

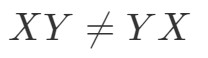
Protože máme

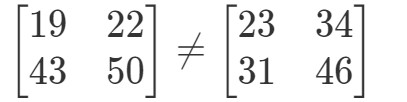
Tyto dvě matice jsou zcela odlišné.

Nyní zbývá ještě několik vlastností násobení matic. Tyto vlastnosti se však týkají nulové a identitní matice.

Násobení matic pro nulovou matici

Vlastnost násobení matic pro nulovou matici říká následující:

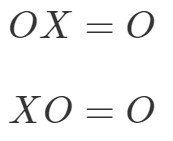
kde OOO je nulová matice.

To znamená, že pokud vynásobíte nulovou matici jinou nenulovou maticí, dostanete nulovou matici. Ověřme si, zda to platí, na příkladu:

Úkol 9: Ukažte, že rovnice OX=OOX = OOX=O a XO=OXO = OXO=O platí, jestliže:

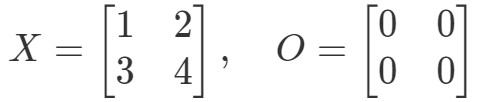
Nejprve se podívejme na rovnici

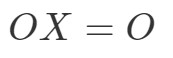
Všimněte si, že výpočet OXOXOX nám dává:

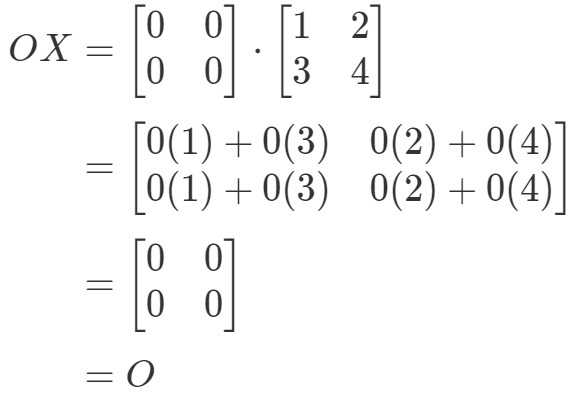
Vidíme, že OX=OOX = OOX=O, takže rovnice platí. Podobně když vypočítáme XOXOXO, dostaneme:

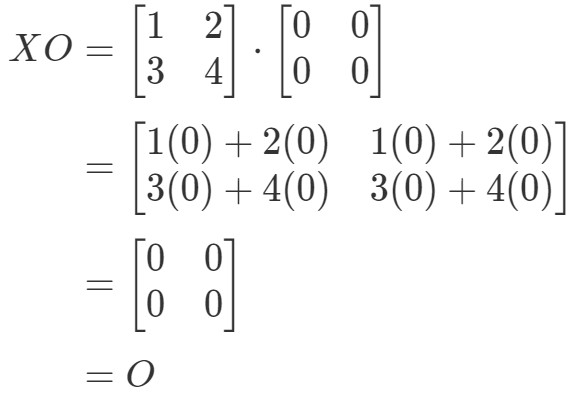
Vidíme, že rovnice XO=OXO = OXO=O platí, takže jsme hotovi.

Násobení matice pro identickou matici

A co nyní s vlastností násobení matice pro identické matice? Inu, tato vlastnost říká následující:

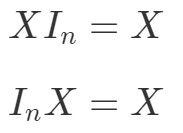
kde InI_{n}In je n×nn \krát nn×n matice identity. O tom, že následující rovnice skutečně platí, se opět můžeme přesvědčit na příkladu.

Otázka 10: Ukažte, že rovnice XI2=XX I_{2} = XXI2=X a I2X=XI_{2}. X = XI2X=X platí s následujícími maticemi

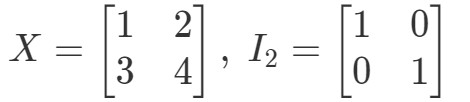
Takže pro rovnici XI2=XX I_{2} = XXI2=X máme:

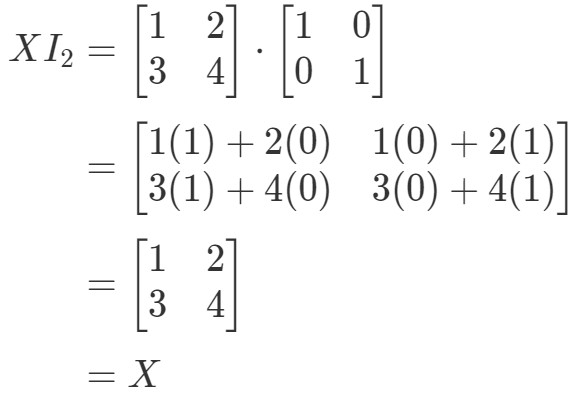
Takže rovnice platí. Podobně jako u rovnice I2X=XI_{2}X = XI2X=X máme:

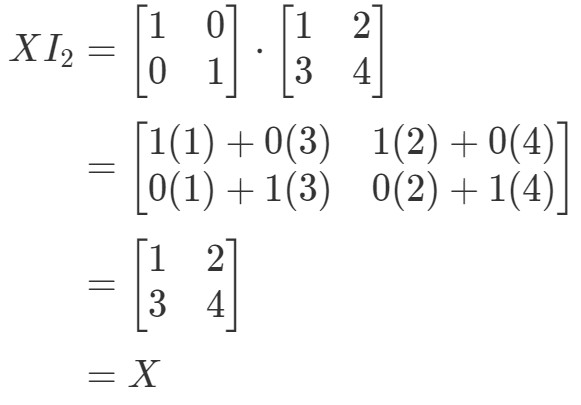
Rovnice opět platí. Tím jsme s otázkou skončili, obě rovnice platí a tím jsme uzavřeli všechny vlastnosti násobení matic. Pokud se nyní chcete podívat na reálnou aplikaci násobení matic, pak vám doporučuji podívat se na tento článek.

https://www.mathsisfun.com/algebra/matrix-multiplying.html

.