Free Press

Mnożenie macierzy

Istnieją dokładnie dwa sposoby mnożenia macierzy. Pierwszy sposób polega na mnożeniu macierzy przez skalar. Jest to znane jako mnożenie skalarne. Drugi sposób polega na mnożeniu macierzy przez inną macierz. Jest to znane jako mnożenie macierzy.

Mnożenie skalarne

Mnożenie skalarne jest w rzeczywistości bardzo prostą operacją na macierzach. Aby pomnożyć skalar przez macierz, po prostu bierzemy skalar i mnożymy go do każdego wpisu w macierzy. Zróbmy przykład.

Pytanie 1: Oblicz 2A2A2A, jeśli

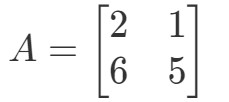
Pytanie to prosi nas o znalezienie odpowiedzi na pytanie, czym jest 2A2A2A. Innymi słowy, znajdujemy

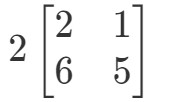
Zauważ, że jeśli pomnożymy 2 do każdego wpisu w macierzy, to otrzymamy:

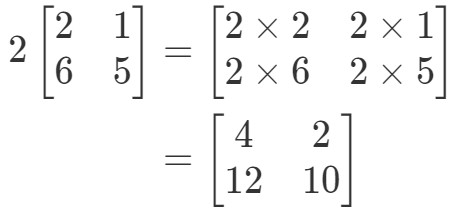
Bardzo proste! Zróbmy jeszcze jedno.

Pytanie 2: Oblicz 0A0A0A, jeśli

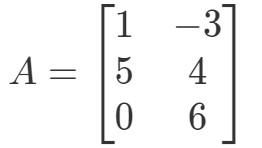
Ponownie, próbujemy znaleźć 0A0A0A. Oznacza to, że będziemy szukać odpowiedzi na

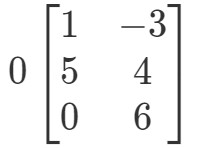
Macierz będzie miała dziwny kształt, ale koncepcja pozostaje ta sama. Nadal będziemy mnożyć skalar 0 do każdego wpisu w macierzy. W ten sposób otrzymamy:

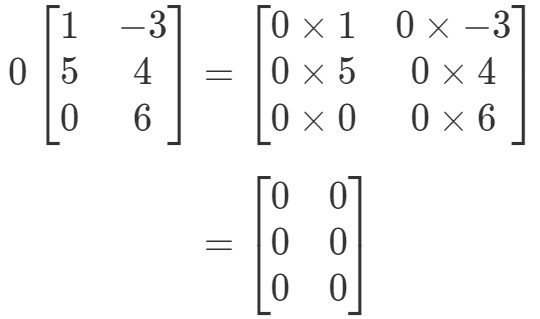
Zauważ, że wszystkie pozycje w macierzy są 0. Jest to znane jako macierz zerowa, która jest 3 x 2.

Teraz, gdy jesteśmy bardzo zaznajomieni z mnożeniem skalarnym, dlaczego nie przejdziemy do mnożenia macierzowego?

Jak mnożyć macierze

Aby pomnożyć macierz przez inną macierz, musimy najpierw dowiedzieć się, czym jest iloczyn kropkowy.

Co to jest iloczyn kropkowy?

Iloczyn kropkowy (znany również jako mnożenie wektorowe) jest sposobem obliczania iloczynu dwóch wektorów. Na przykład, niech dwa wektory będą następujące:

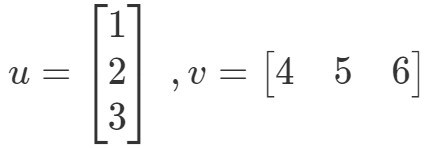
Jak mógłbym pomnożyć te dwa wektory? Po prostu pomnóż odpowiednie pozycje, a następnie dodaj produkty razem. Innymi słowy,

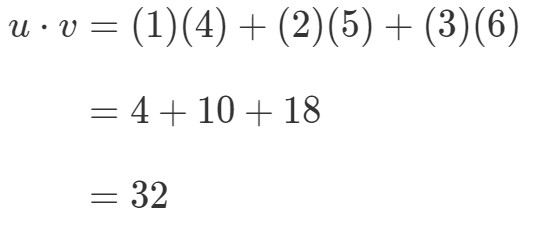
W ten sposób otrzymujemy pojedynczą wartość z mnożenia wektorów. Zauważmy jednak, że te dwa wektory mają taką samą liczbę wpisów. Co jeśli jeden z wektorów ma inną liczbę wpisów niż drugi? Na przykład, niech

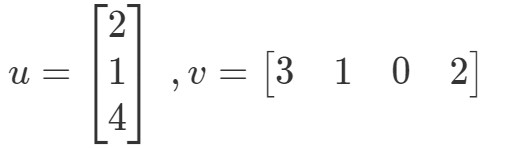
Jeśli miałbym pomnożyć odpowiadające sobie zapisy i dodać je do siebie, to otrzymam:

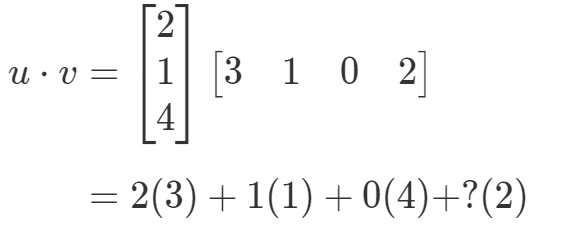
Jest tu pewien problem. Pierwsze trzy wpisy mają odpowiadające im wpisy, z którymi można je pomnożyć, ale ostatni wpis nie ma. Co więc robimy w tym miejscu? Odpowiedź brzmi: nie możemy tu nic zrobić. Oznacza to po prostu, że nie możemy obliczyć iloczynu punktowego tych dwóch wektorów.

Więc podsumowując, nie możemy znaleźć iloczynu punktowego dwóch wektorów, które mają różne liczby wpisów. Muszą one mieć taką samą liczbę wpisów.

Mnożenie macierzowe 2 x 2

Więc jaki był sens uczenia się iloczynu kropkowego? Cóż, będziemy używać iloczynu kropkowego, gdy będziemy mnożyć dwie macierze razem. Podczas mnożenia macierzy z inną macierzą, chcemy traktować wiersze i kolumny jako wektor. Dokładniej, chcemy traktować każdy wiersz w pierwszej macierzy jako wektor, a każdą kolumnę w drugiej macierzy jako wektor. Zróbmy przykład.

Pytanie 3: Znajdź A∙BA ∙B jeśli

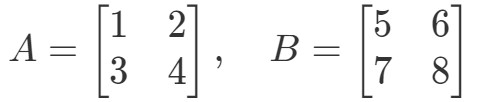
Mnożąc dwie macierze otrzymamy:

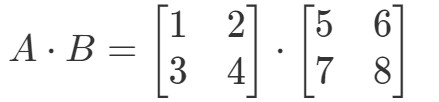
Teraz wiersze i kolumny, na których się skupiamy to

gdzie r1r_{1}r1 jest pierwszym rzędem, r2r_{2}r2 jest drugim rzędem, a c1,c2c_{1}, c_{2}c1,c2 są pierwszą i drugą kolumną. Teraz będziemy traktować każdy wiersz i kolumnę, które widzimy tutaj jako wektor.

Zauważ tutaj, że mnożenie macierzy 2 x 2 z inną macierzą 2 x 2 daje macierz 2 x 2. Innymi słowy, macierz, którą otrzymamy powinna mieć 4 wpisy.

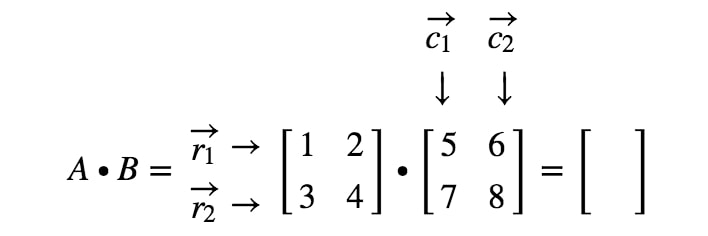
Jak dokładnie otrzymamy pierwszy wpis? Cóż, zauważ, że pierwszy wpis znajduje się w pierwszym wierszu i pierwszej kolumnie. Więc po prostu weźmiemy iloczyn kropkowy r1r_{1}r1 i c1c_{1}c1. Tak więc, pierwszy wpis będzie

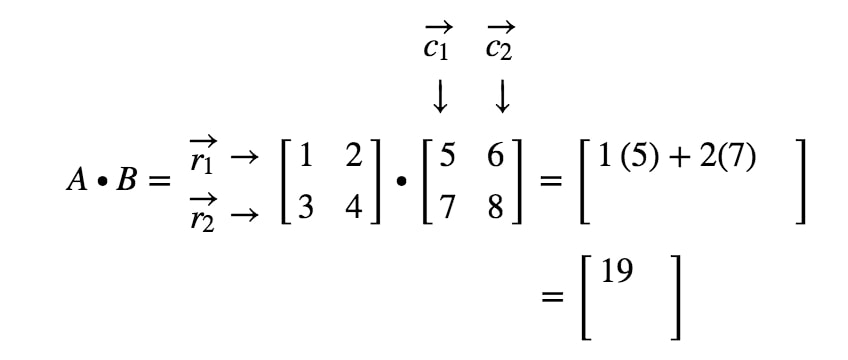
Jak tym razem otrzymamy drugi wpis? Zauważ, że drugi wpis znajduje się w pierwszym wierszu i drugiej kolumnie. Zatem po prostu weźmiemy iloczyn kropkowy r1r_{1}r1 i c2c_{2}c2. Tak więc drugi wpis będzie

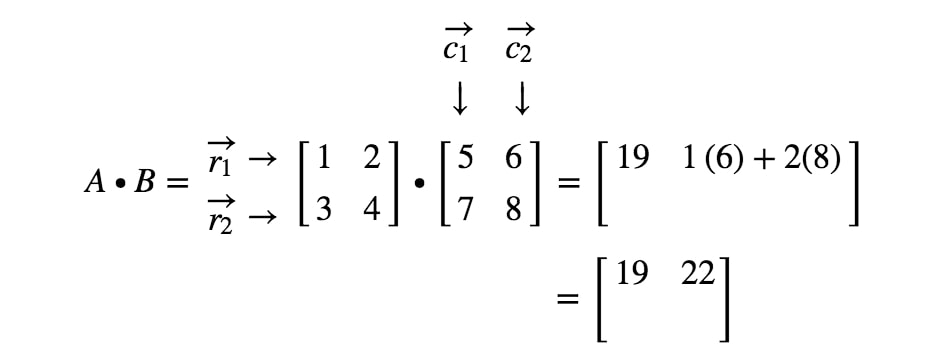
Teraz użyjemy tej samej strategii, aby poszukać dwóch ostatnich wpisów. Zauważmy, że drugi ostatni wpis znajduje się w 2^{nd}2. wierszu i 1^{st}1. kolumnie, a ostatni wpis znajduje się w 2^{nd}2. wierszu i 2^{nd}2. kolumnie. Bierzemy więc iloczyn punktowy r2r_{2}r2 i c1c_{1}c1 oraz iloczyn punktowy r2r_{2}r2 i c2c_{2}c2. Daje nam to:

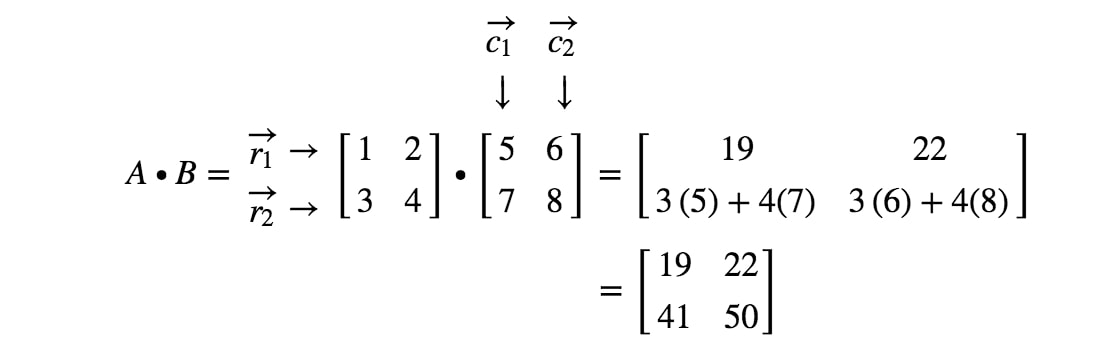
Teraz skończyliśmy! Oto co otrzymamy, gdy będziemy mnożyć macierze 2 x 2. Ogólnie, wzór mnożenia macierzy dla macierzy 2 x 2 to

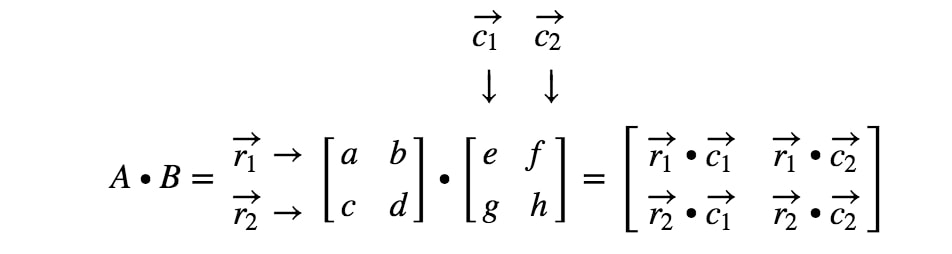
Mnożenie macierzy 3 x 3

Teraz proces mnożenia macierzy 3 x 3 jest bardzo podobny do procesu mnożenia macierzy 2 x 2. Ponownie, dlaczego nie zrobimy przykładu mnożenia macierzy?

Pytanie 4:Znajdź A∙BA ∙B jeśli

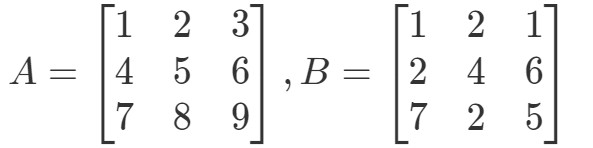
Po pierwsze, zauważ, że pomnożenie ich powinno dać nam kolejną macierz 3 x 3. Innymi słowy,

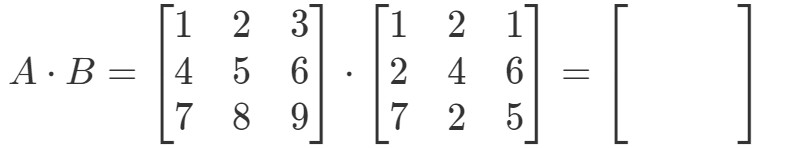
Naznaczmy teraz wszystkie nasze wiersze w pierwszej macierzy i kolumny w drugiej macierzy.

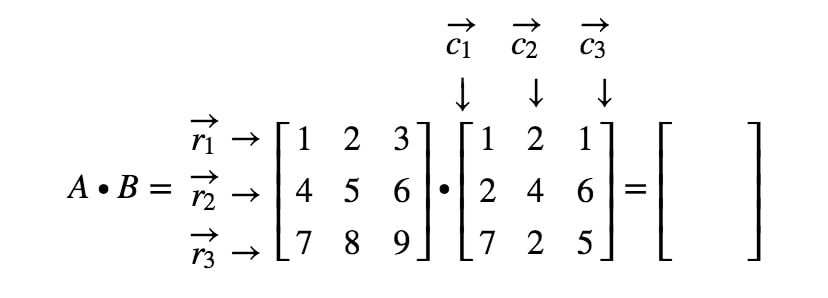
Zauważmy, że pierwszy wpis macierzy znajduje się w 1.^{st}1. wierszu i 1.^{st}1. kolumnie, więc wykonujemy iloczyn kropkowy r1r_{1}r1 i c1c_{1}c1. To daje nam:

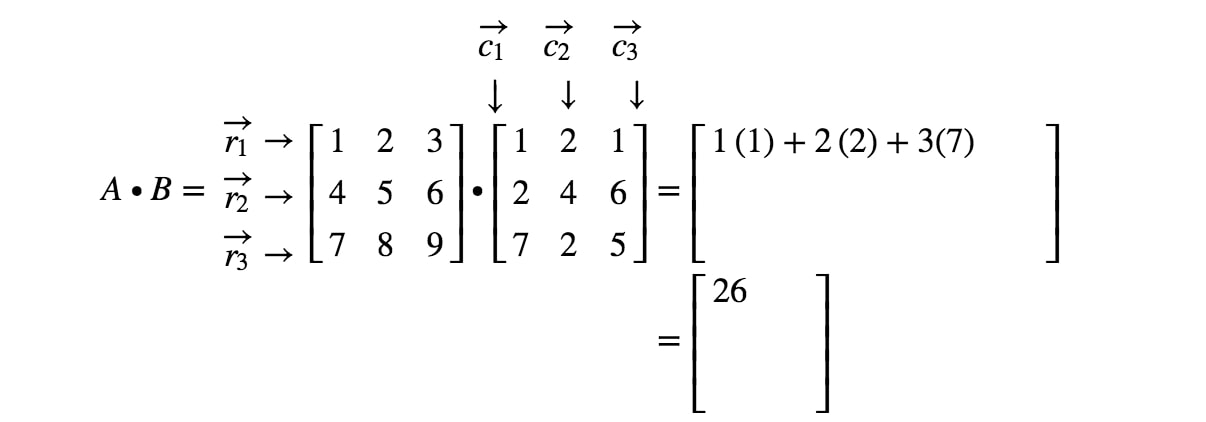
Zauważmy teraz, że drugi wpis macierzy znajduje się w 11^{st}1 wierszu i 2^{nd}2 kolumnie. Zatem wykonujemy iloczyn punktowy r1r_{1}r1 i c2c_{2}c2. To daje nam:

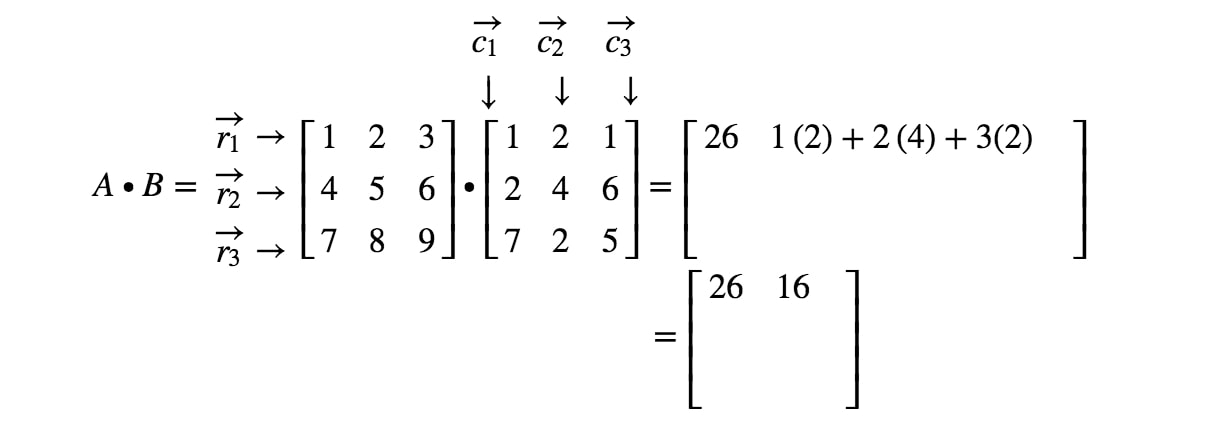
Jeśli nadal będziemy lokalizować wszystkie wpisy i wykonywać iloczyn kropkowy odpowiadający wierszom i kolumnom, to otrzymamy wynik końcowy.

Skończyliśmy! Zauważ, że im większe są macierze, tym bardziej żmudne staje się mnożenie macierzy. Dzieje się tak dlatego, że mamy do czynienia z coraz większą ilością liczb! Ogólnie, wzór na mnożenie macierzy dla macierzy 3 x 3 to

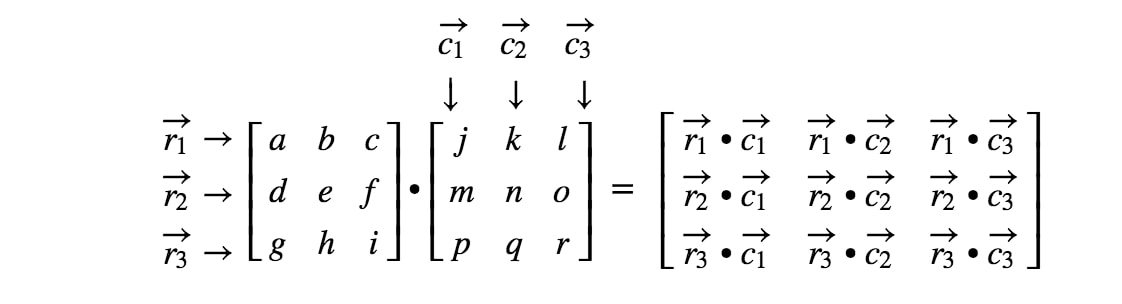
Jak mnożyć macierze o różnych wymiarach?

Do tej pory mnożyliśmy macierze o tych samych wymiarach. Ponadto wiemy, że mnożenie dwóch macierzy o tych samych wymiarach daje macierz o tych samych wymiarach. Ale co się stanie, jeśli pomnożymy macierz o różnych wymiarach? Skąd będziemy wiedzieć, jakie wymiary ma wyliczona macierz? Po pierwsze, musimy zobaczyć, że mnożenie macierzy daje zdefiniowaną macierz.

Is the Matrix Defined?

Są przypadki, w których nie jest możliwe pomnożenie dwóch macierzy razem. Dla tych przypadków, nazywamy macierz niezdefiniowaną. Jak możemy stwierdzić, że są one niezdefiniowane?

Iloczyn dwóch macierzy jest zdefiniowany tylko wtedy, gdy liczba kolumn pierwszej macierzy jest równa liczbie wierszy drugiej macierzy.

Postarajmy się wykorzystać tę definicję w tym przykładzie.

Pytanie 5: Niech

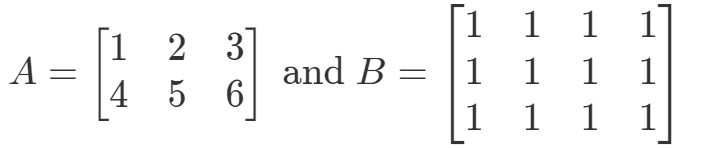
Czy macierz A∙BA jest zdefiniowana?

Po pierwsze zauważ, że pierwsza macierz ma 3 kolumny. Również druga macierz ma 3 wiersze. Ponieważ obie są równe 3, to wiem, że A∙BA ∙bullet BA∙B jest zdefiniowana.

Teraz, gdy wiemy, że jest zdefiniowana, jak moglibyśmy poznać wymiary A∙BA ∙bullet BA∙B?

Własność wymiaru

Aby znaleźć wymiary A∙BA ∙bullet BA∙B, musimy najpierw spojrzeć na wymiary i oddzielnie.

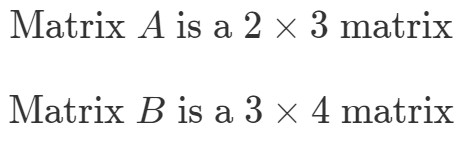
Teraz umieścimy wymiary macierzy obok siebie w ten sposób:

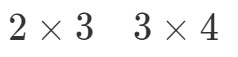
What we are going to do now is taking the first number and the last number and combine it to get the dimensions of A∙BA ∙bullet BA∙B. Zobacz, że pierwsza liczba to 2, a ostatnia to 4. Zatem wymiary A∙BA ∙bullet BA∙B będą:

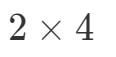
Teraz, gdy znamy wymiary macierzy, możemy po prostu obliczyć każdy wpis używając iloczynów kropkowych. W ten sposób otrzymamy:

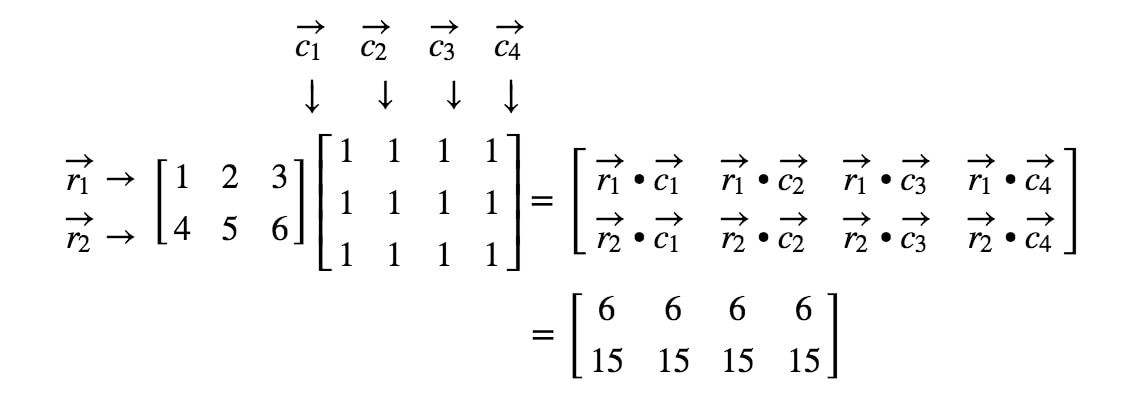
Teraz, gdy wiemy już jak dobrze mnożyć macierze, dlaczego nie przyjrzeć się niektórym regułom mnożenia macierzy?

Właściwości mnożenia macierzy

Jakie właściwości ma mnożenie macierzy? Po pierwsze, zdefiniujmy wszystko formalnie.

Niech X,Y,ZX, Y, ZX,Y,Z będą macierzami, InI_{n}In będzie macierzą tożsamości, a OnO_{n}On będzie macierzą zerową. Jeśli wszystkie pięć z tych macierzy ma równe wymiary, to mamy następujące własności mnożenia macierzy:

Własność asocjacyjna mówi, że kolejność mnożenia nie ma znaczenia. Innymi słowy, obliczenie X∙YX ∙bullet YX∙Y, a następnie pomnożenie przez ZZZ da taki sam wynik, jak obliczenie Y∙ZY ∙bullet ZY∙Z, a następnie pomnożenie przez XXX. Zróbmy przykład.

Pytanie 6: Pokaż, że własność asocjacyjna działa z tymi macierzami:

Patrząc na lewą stronę równania we własności asocjacyjnej, widzimy, że (XY)Z(XY)Z(XY)Z daje:

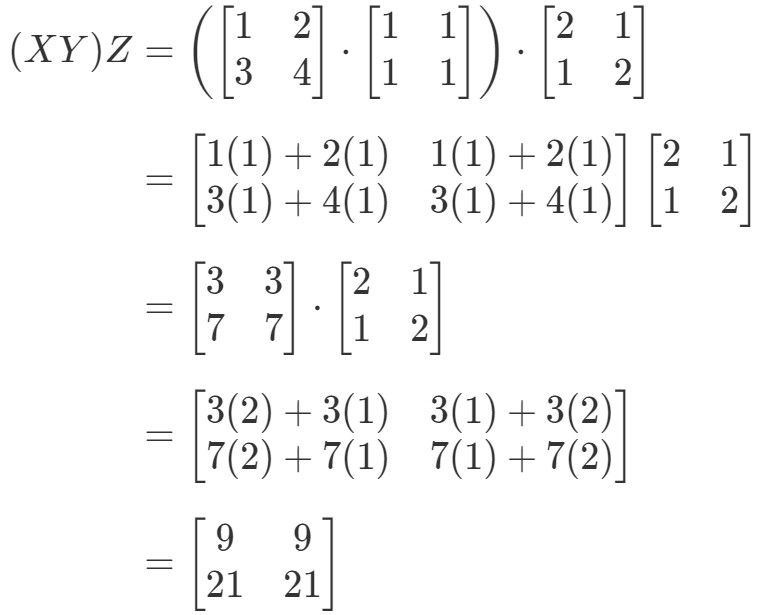
Patrząc teraz na prawą stronę równania we własności asocjacyjnej, widzimy, że X(YZ)X(YZ)X(YZ) daje:

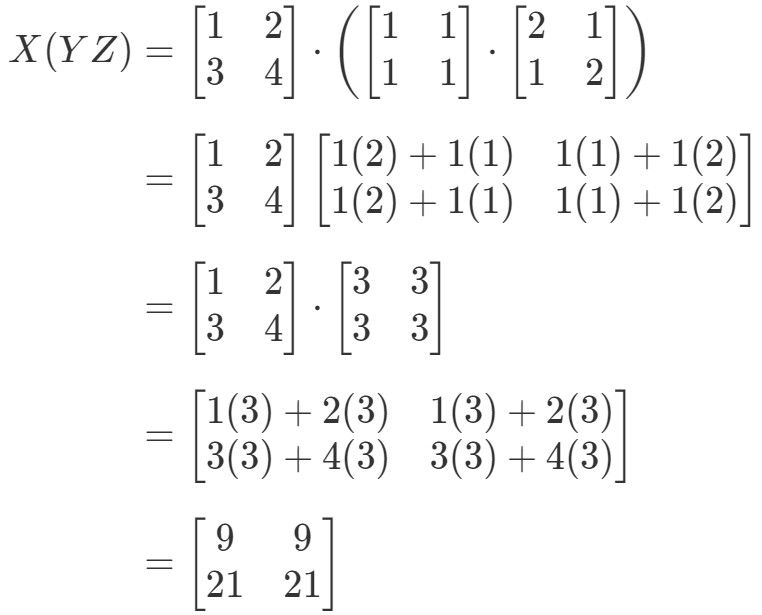
Zobacz jak lewa i prawa strona równania są równe. Stąd wiemy, że własność asocjacyjna faktycznie działa! Ponownie, oznacza to, że kolejność mnożenia macierzy nie ma znaczenia!

Teraz następną własnością jest własność dystrybucyjna. Własność dystrybucyjna mówi, że:

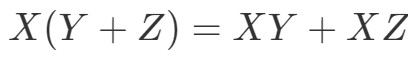
Widzimy, że możemy używać techniki foliacji również dla macierzy. Aby pokazać, że ta własność działa, zróbmy przykład.

Pytanie 7: Pokaż, że własność rozdzielcza działa dla następujących macierzy:

Zauważmy, że lewa strona równania to X(Y+Z)X(Y + Z)X(Y+Z). Stąd obliczenie tego daje nam:

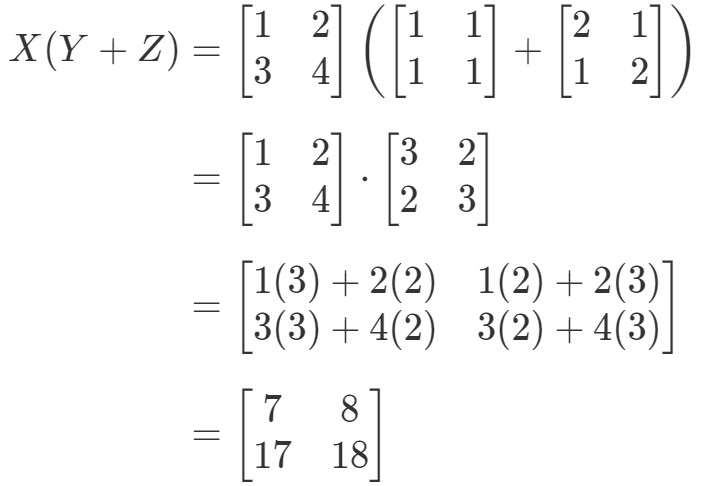
Sprawdźmy teraz, czy prawa strona równania daje nam dokładnie to samo. Zauważmy, że prawa strona równania to XY+XZXY + XZXY+XZ. Obliczenie tego daje nam:

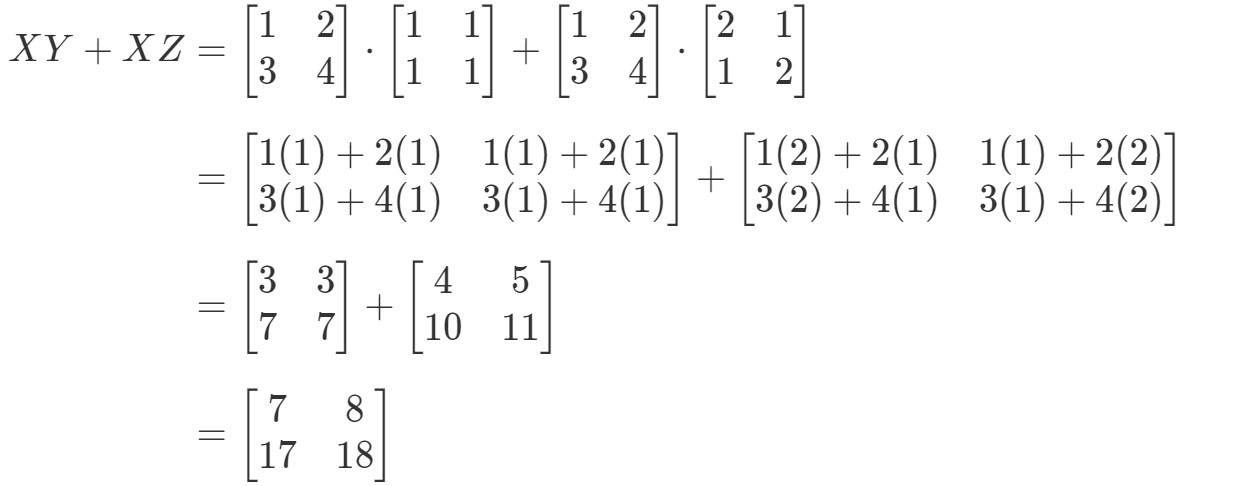
Zauważ, że lewa strona równania jest dokładnie taka sama jak prawa strona równania. Stąd możemy potwierdzić, że własność rozdzielcza rzeczywiście działa.

Is Matrix Multiplication Commutative?

Wiemy, że mnożenie macierzy spełnia zarówno własność asocjacyjną, jak i rozdzielczą, jednak w ogóle nie mówiliśmy o własności komutacyjnej. Czy to oznacza, że mnożenie macierzowe jej nie spełnia? W rzeczywistości nie spełnia, a możemy to sprawdzić na przykładzie.

Pytanie 8: Jeśli mnożenie macierzowe jest komutatywne, to musi być prawdziwe:

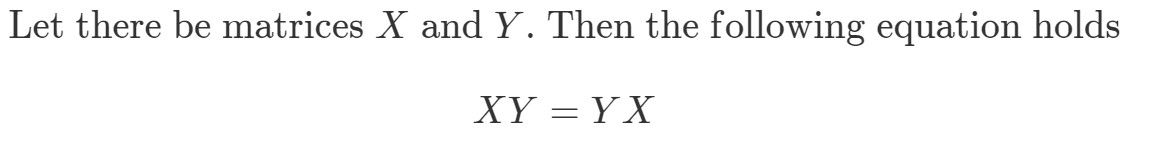
Wykaż, że XYeqYXXY eq YXXYeqYX if

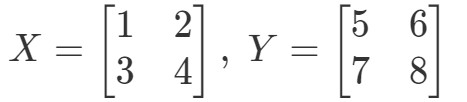
Najpierw obliczamy lewą stronę równania. Obliczając XYXYXY otrzymujemy:

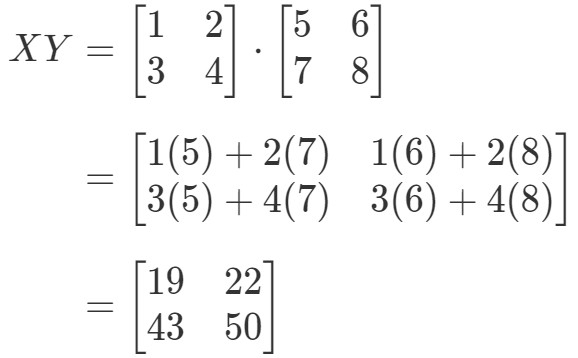
Teraz obliczając prawą stronę równania, mamy:

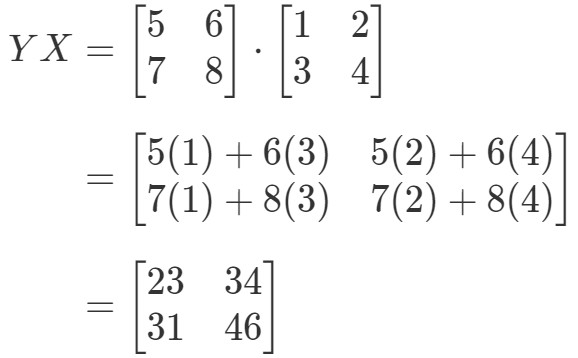
Jak widać,

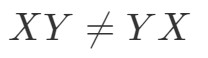
Ponieważ mamy

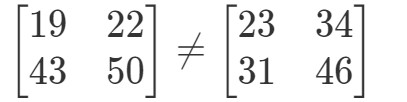
Te dwie macierze są zupełnie inne.

Teraz pozostaje jeszcze kilka własności mnożenia macierzy. Jednak te własności dotyczą macierzy zerowych i tożsamościowych.

Mnożenie macierzy dla macierzy zerowej

Własność mnożenia macierzy dla macierzy zerowej mówi co następuje:

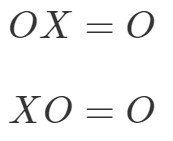
gdzie OOO jest macierzą zerową.

Oznacza to, że gdybyśmy mieli pomnożyć macierz zerową przez inną niezerową, to otrzymamy macierz zerową. Sprawdźmy na przykładzie, czy to prawda.

Pytanie 9: Pokaż, że równanie OX=OOX = OOX=O i XO=OXO = OXO=O zachodzi, jeśli:

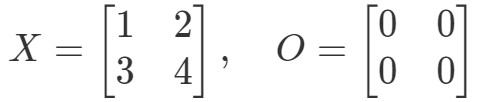
Spójrzmy najpierw na równanie

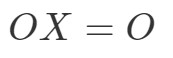
Zauważmy, że obliczając OXOXOX otrzymamy:

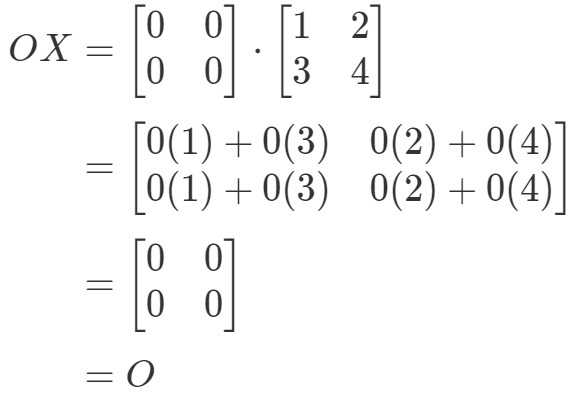
Widzimy, że OX=OOX = OOX=O, więc równanie zachodzi. Podobnie, jeśli obliczymy XOXOXO, otrzymamy:

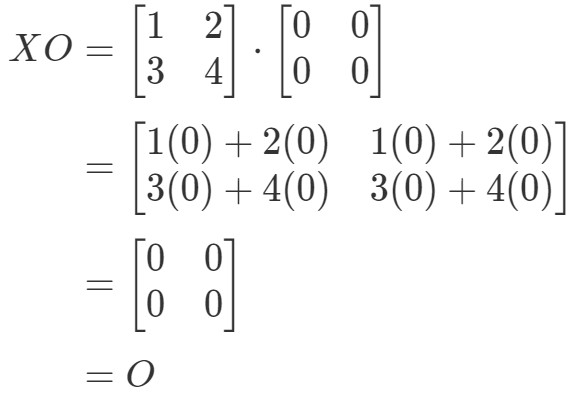
Widzimy, że równanie XO=OXO = OXO=O zachodzi, więc skończyliśmy.

Mnożenie macierzy dla macierzy tożsamości

A co z własnością mnożenia macierzy dla macierzy tożsamości? Otóż własność ta mówi, co następuje:

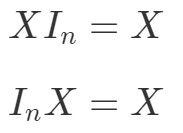
gdzie InI_{n}In jest macierzą tożsamości n×nn ̨ razy nn×n. Ponownie możemy przekonać się na przykładzie, że poniższe równania są prawdziwe.

Pytanie 10: Pokaż, że równania XI2=XX I_{2} = XXI2=X oraz I2X=XI_{2} X = XI2X=X zachodzi dla następujących macierzy

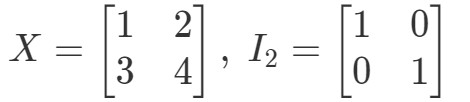
Więc dla równania XI2=XX I_{2} = XXI2=X, mamy:

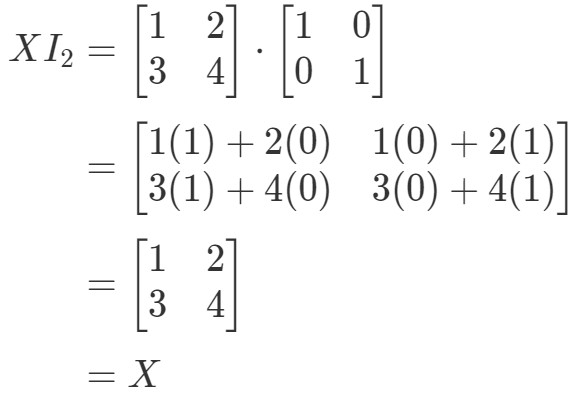
Więc równanie spełnia warunki. Podobnie jak w przypadku równania I2X=XI_{2}X = XI2X=X, mamy:

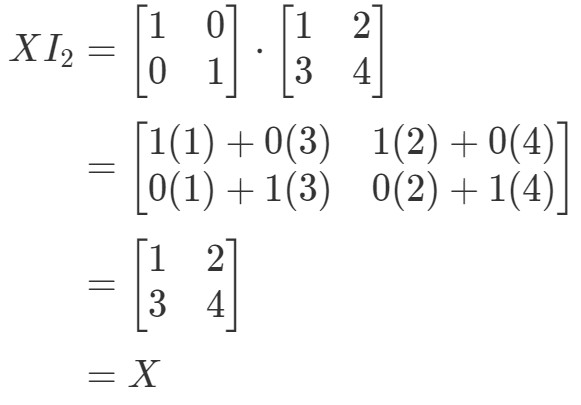
Ponownie, równanie zachodzi. Skończyliśmy więc z tym pytaniem, a oba równania spełniają warunki. Teraz, jeśli chcesz spojrzeć na prawdziwe zastosowanie mnożenia macierzy, to polecam spojrzeć na ten artykuł.

https://www.mathsisfun.com/algebra/matrix-multiplying.html