Free Press

Multiplicación de matrices

Hay exactamente dos formas de multiplicar matrices. La primera forma es multiplicar una matriz por un escalar. Esto se conoce como multiplicación escalar. La segunda forma es multiplicar una matriz con otra matriz. Esto se conoce como multiplicación matricial.

Multiplicación escalar

La multiplicación escalar es en realidad una operación matricial muy sencilla. Para multiplicar un escalar con una matriz, simplemente tomamos el escalar y lo multiplicamos por cada entrada de la matriz. Hagamos un ejemplo.

Pregunta 1: Calcular 2A2A2A si

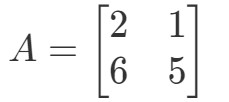
La pregunta nos está pidiendo que averigüemos qué es 2A2A2A. En otras palabras, estamos encontrando

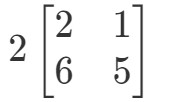
Nota que si vamos a multiplicar 2 a cada entrada de la matriz, obtenemos que:

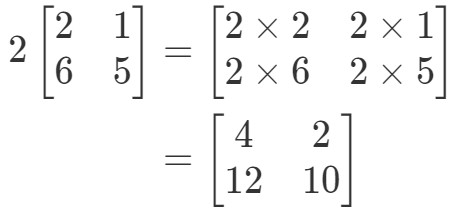
¡Muy sencillo! Hagamos otra.

Pregunta 2: Calcula 0A0A0A si

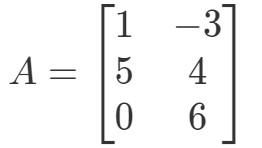
De nuevo, estamos tratando de encontrar 0A0A0A. Esto significa que estaremos buscando la respuesta a

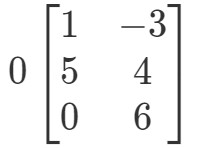
La matriz tendrá una forma extraña, pero el concepto sigue siendo el mismo. Seguiremos multiplicando el escalar 0 a cada entrada de la matriz. Haciendo esto nos da:

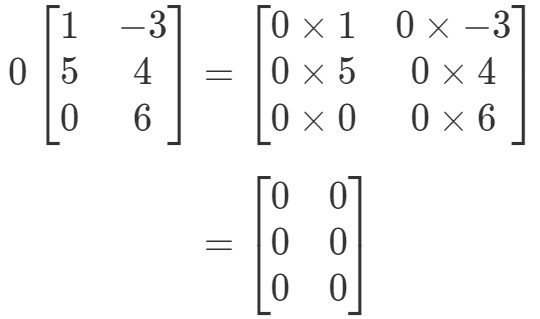
Nota que todas las entradas de la matriz son 0. Esto se conoce como una matriz cero que es 3 x 2.

Ahora que estamos muy familiarizados con la multiplicación escalar, ¿por qué no pasamos a la multiplicación matricial?

Cómo multiplicar matrices

Para multiplicar una matriz por otra matriz, primero tenemos que aprender qué es el producto punto.

¿Qué es el producto punto?

El producto punto (también conocido como multiplicación vectorial) es una forma de calcular el producto de dos vectores. Por ejemplo, dejemos que los dos vectores sean:

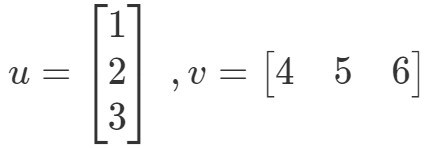
¿Cómo multiplicaría estos dos vectores? Simplemente multiplica las entradas correspondientes, y suma los productos. En otras palabras,

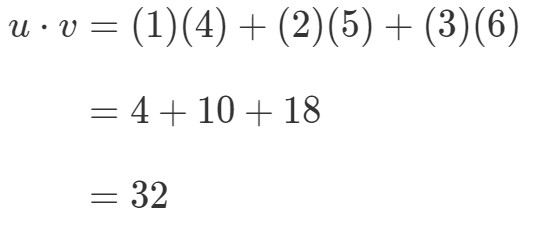
Así que obtenemos un único valor al multiplicar los vectores. Sin embargo, fíjate en que los dos vectores tienen el mismo número de entradas. ¿Qué pasa si uno de los vectores tiene un número diferente de entradas que el otro? Por ejemplo, dejemos que

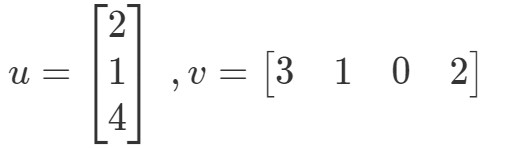
Si multiplicara las entradas correspondientes y las sumara todas, entonces obtendría:

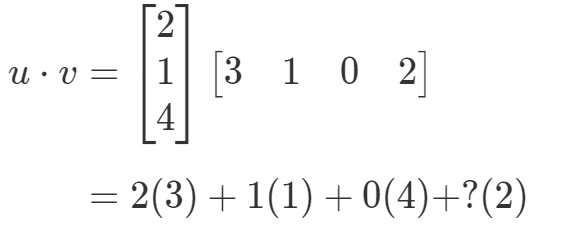
Hay un problema aquí. Las tres primeras entradas tienen entradas correspondientes para multiplicar, pero la última entrada no. Entonces, ¿qué hacemos aquí? La respuesta es que no podemos hacer nada aquí. Esto sólo significa que no podemos calcular el producto punto de estos dos vectores.

Así que en conclusión, no podemos encontrar el producto punto de dos vectores que tienen diferentes números de entradas. Deben tener el mismo número de entradas.

Multiplicación de matrices 2 x 2

Entonces, ¿qué sentido tenía aprender el producto punto? Bueno, usaremos el producto punto cuando multipliquemos dos matrices juntas. Al multiplicar una matriz con otra matriz, queremos tratar las filas y las columnas como un vector. Más específicamente, queremos tratar cada fila de la primera matriz como vectores, y cada columna de la segunda matriz como vectores. Hagamos un ejemplo.

Pregunta 3: Encuentra A∙BA \bullet BA∙B if

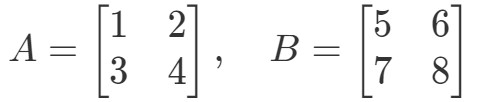
La multiplicación de las dos matrices nos dará:

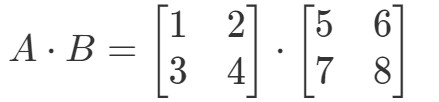
Ahora las filas y las columnas en las que nos centramos son

donde r1r_{1}r1 es la primera fila, r2r_{2}r2 es la segunda fila, y, c1,c2c_{1}, c_{2}c1,c2 son primera y segunda columnas. Ahora vamos a tratar cada fila y columna que vemos aquí como un vector.

Nota aquí que al multiplicar una matriz de 2 x 2 con otra matriz de 2 x 2 se obtiene una matriz de 2 x 2. En otras palabras, la matriz que obtenemos debe tener 4 entradas.

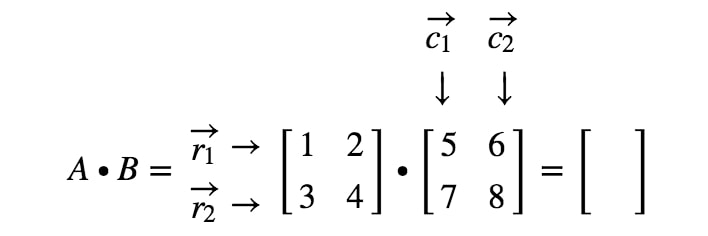
¿Cómo obtenemos exactamente la primera entrada? Bien, observa que la primera entrada se encuentra en la primera fila y la primera columna. Así que simplemente tomamos el producto punto de r1r_{1}r1 y c1c_{1}c1. Así, la primera entrada será

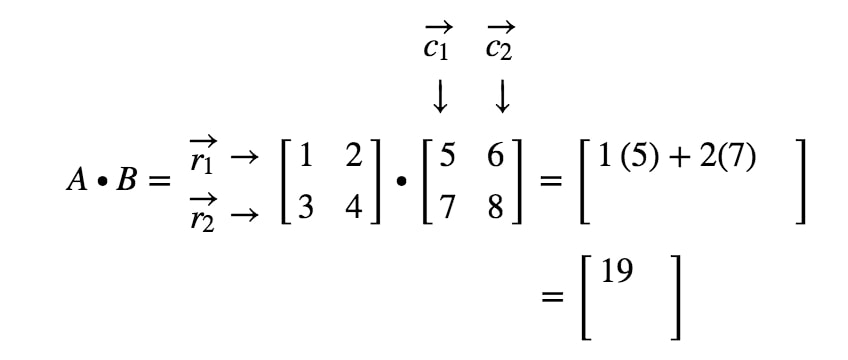
¿Cómo obtenemos la segunda entrada esta vez? Bien, observa que la ubicación de la segunda entrada está en la primera fila y la segunda columna. Así que simplemente tomamos el producto punto de r1r_{1}r1 y c2c_{2}c2. Así, la segunda entrada será

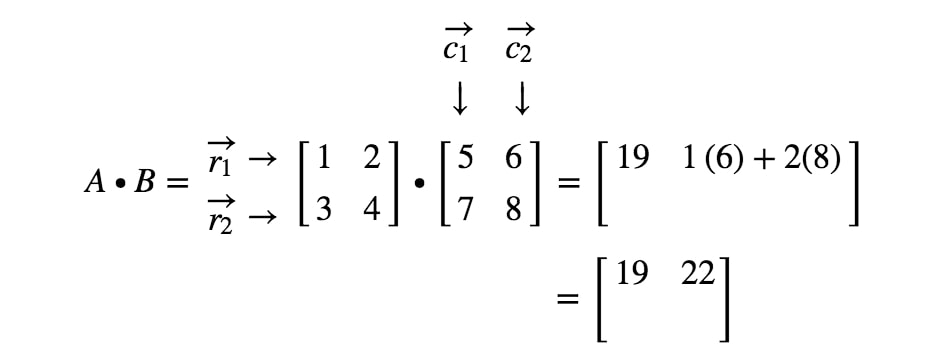
Ahora vamos a utilizar la misma estrategia para buscar las dos últimas entradas. Observa que la penúltima entrada se encuentra en la 2ª2^{nd}2ª fila y 1ª1^{st}1ª columna, y la última entrada se encuentra en la 2ª2^{nd}2ª fila y 2ª2^{nd}2ª columna. Así que tomamos el producto punto de r2r_{2}r2 y c1c_{1}c1, y el producto punto de r2r_{2}r2 y c2c_{2}c2. Esto nos da:

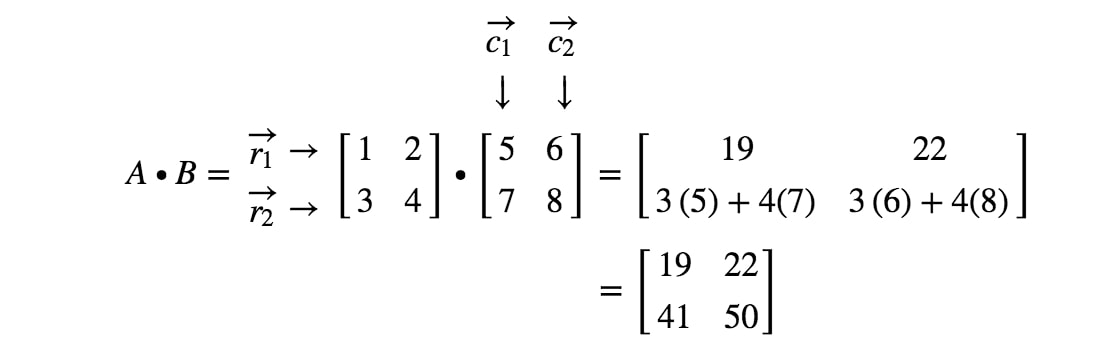
¡Ya hemos terminado! Esto es lo que obtenemos cuando multiplicamos matrices de 2 x 2. En general, la fórmula de multiplicación de matrices de 2 x 2 es

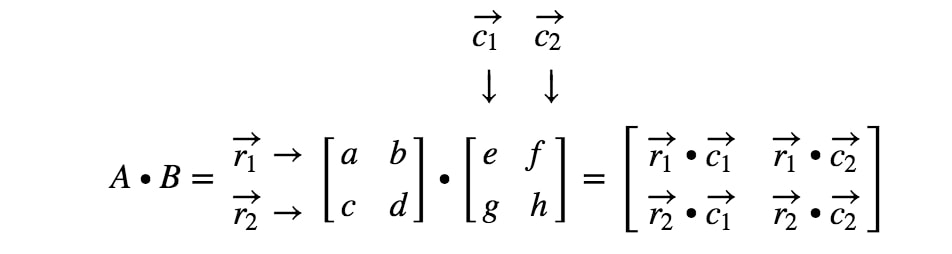
Multiplicación de matrices de 3 x 3

Ahora el proceso de una multiplicación de matrices de 3 x 3 es muy similar al proceso de una multiplicación de matrices de 2 x 2. De nuevo, ¿por qué no hacemos un ejemplo de multiplicación de matrices?

Pregunta 4:Encuentra A∙BA \bullet BA∙B if

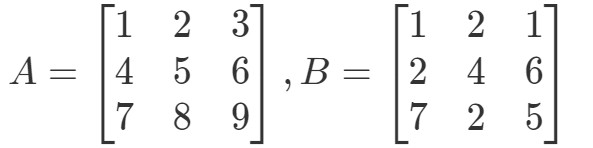
Primero, fíjate en que al multiplicarlas deberíamos obtener otra matriz de 3 x 3. En otras palabras,

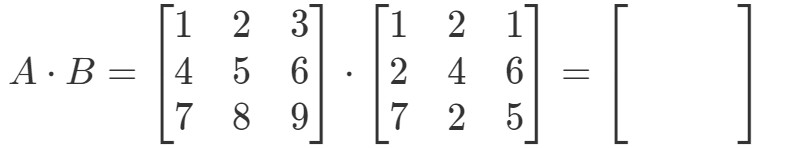
Ahora vamos a etiquetar todas nuestras filas en la primera matriz y las columnas en la segunda matriz.

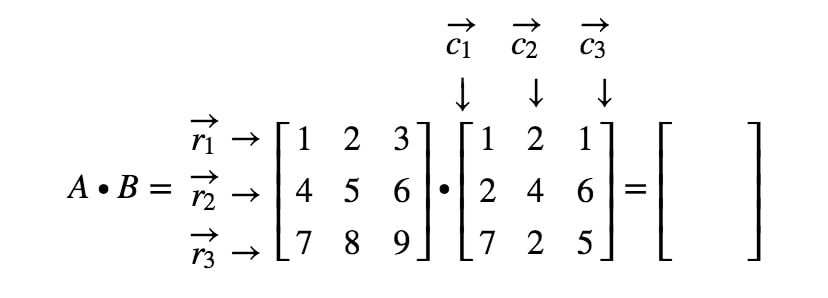
Nota que la primera entrada de la matriz se encuentra en la 1ª1^{st}1ª fila y 1ª1^{st}1ª columna, por lo que tomamos el producto punto de r1r_{1}r1 y c1c_{1}c1. Esto nos da:

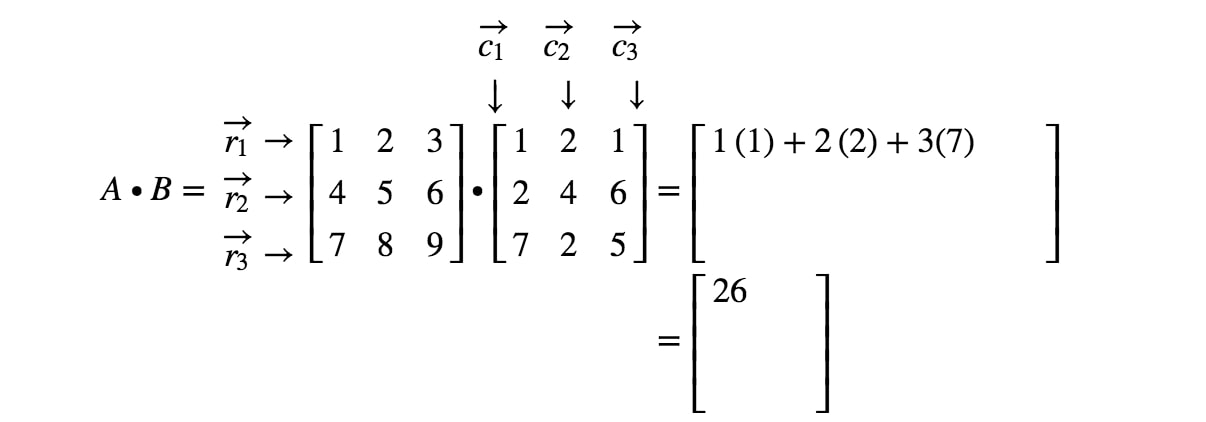
Ahora observe que la segunda entrada de la matriz se encuentra en la 1ª1^{st}1ª fila y 2ª2^{nd}2ª columna. Así, tomamos el producto punto de r1r_{1}r1 y c2c_{2}c2. Esto nos da:

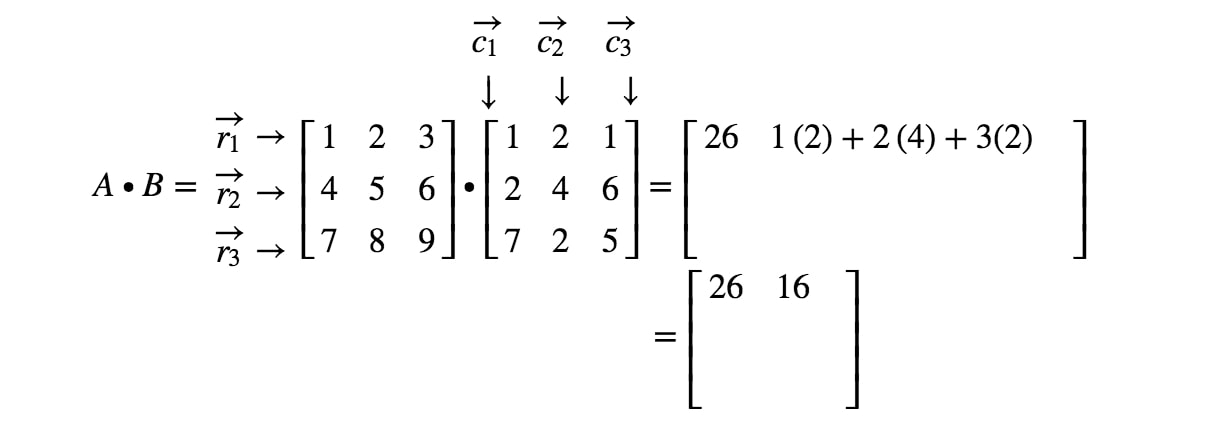
Si vamos a seguir ubicando todas las entradas y haciendo el producto punto correspondiente a las filas y columnas, entonces obtenemos el resultado final.

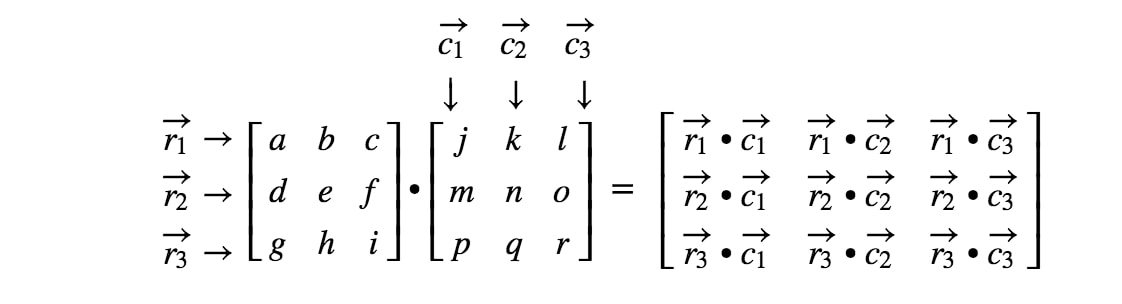
¡Hemos terminado! Observa que cuanto más grandes son las matrices, más tediosa se vuelve la multiplicación de matrices. ¡Esto se debe a que tenemos que tratar con más y más números! En general, la fórmula de multiplicación matricial para matrices de 3 x 3 es

¿Cómo multiplicar matrices con diferentes dimensiones?

Hasta ahora hemos multiplicado matrices con las mismas dimensiones. Además, sabemos que al multiplicar dos matrices con la misma dimensión se obtiene una matriz de las mismas dimensiones. Pero, ¿qué ocurre si multiplicamos una matriz con diferentes dimensiones? ¿Cómo podemos saber las dimensiones de la matriz calculada? Primero, tenemos que ver que multiplicar las matrices da una matriz definida.

¿Está definida la matriz?

Hay casos en los que no es posible multiplicar dos matrices juntas. Para esos casos, llamamos a la matriz indefinida. ¿Cómo podemos saber si están indefinidas?

El producto de dos matrices sólo está definido si el número de columnas de la primera matriz es igual al número de filas de la segunda.

Intentemos utilizar esta definición en este ejemplo.

Pregunta 5: Dejemos

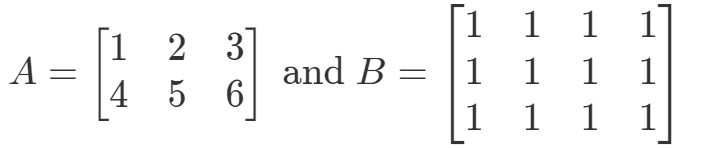
¿Está definida A∙BA \bullet BA∙B?

En primer lugar, observa que la primera matriz tiene 3 columnas. Además, la segunda matriz tiene 3 filas. Como ambas son iguales a 3, entonces sé que A∙BA \bullet BA∙B está definida.

Ahora que sabemos que está definida, ¿cómo podríamos saber las dimensiones de A∙BA \bullet BA∙B?

La propiedad de la dimensión

Para encontrar las dimensiones de A∙BA \bullet BA∙B, tenemos que mirar primero las dimensiones de y por separado.

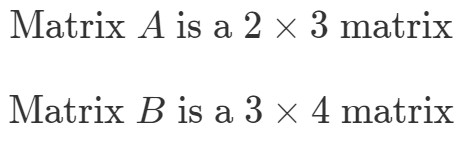
Ahora vamos a poner las dimensiones de las matrices una al lado de la otra así:

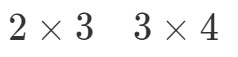
Lo que vamos a hacer ahora es tomar el primer número y el último número y combinarlo para obtener las dimensiones de A∙BA \bullet BA∙B. Observa que el primer número es 2 y el último es 4. Así que las dimensiones de A∙BA \bullet BA∙B serán:

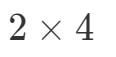
Ahora que conocemos las dimensiones de la matriz, podemos simplemente calcular cada entrada utilizando los productos de punto. Esto nos dará:

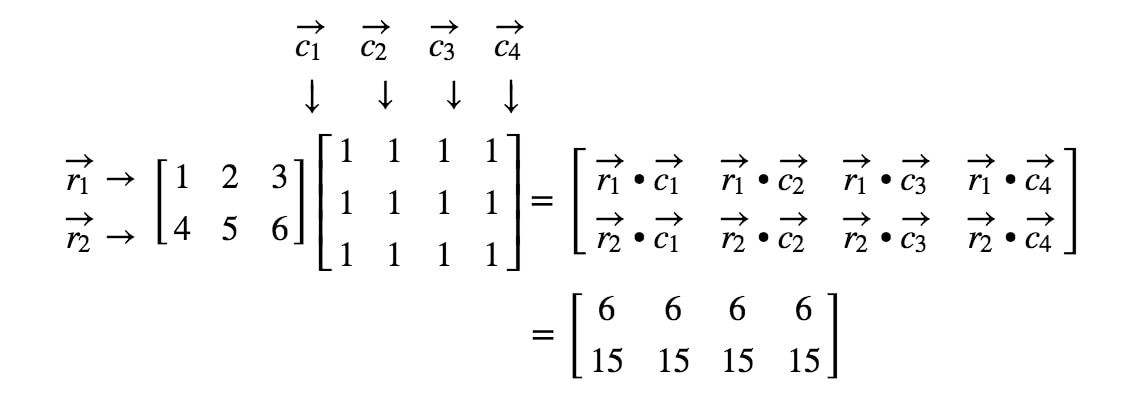
Ahora que sabemos muy bien cómo multiplicar matrices, ¿por qué no echamos un vistazo a algunas reglas de multiplicación matricial?

Propiedades de la multiplicación matricial

Entonces, ¿qué tipo de propiedades tiene realmente la multiplicación matricial? Primero, definamos formalmente todo.

Sea X,Y,ZX, Y, ZX,Y,Z matrices, InI_{n}In sea una matriz identidad, y OnO_{n}On sea una matriz cero. Si las cinco matrices tienen las mismas dimensiones, entonces tendremos las siguientes propiedades de multiplicación de matriz a matriz:

La propiedad asociativa establece que el orden en que se multiplica no importa. En otras palabras, calcular X∙YX \bullet YX∙Y y luego multiplicar con ZZZ te daría el mismo resultado que calcular Y∙ZY \bullet ZY∙Z y luego multiplicar con XXX. Hagamos un ejemplo.

Pregunta 6: Demuestra que la propiedad asociativa funciona con estas matrices:

Mirando el lado izquierdo de la ecuación de la propiedad asociativa, vemos que (XY)Z(XY)Z(XY)Z da:

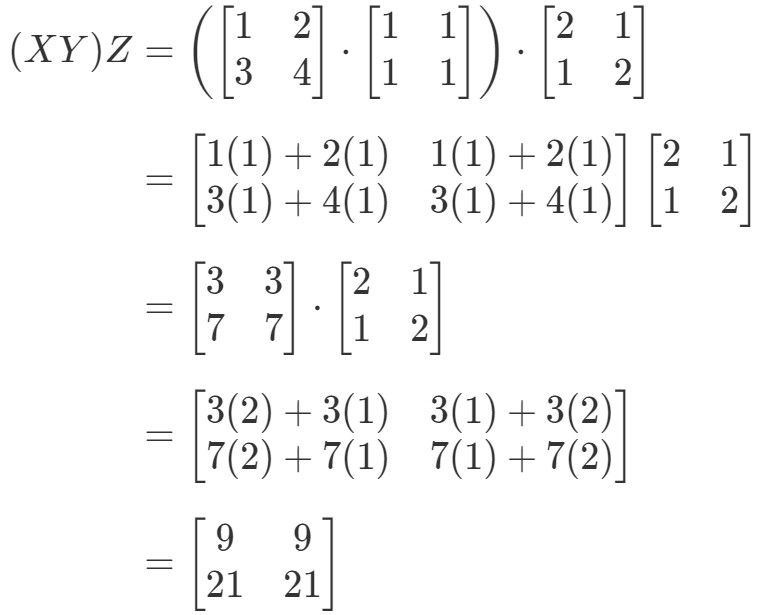
Ahora mirando el lado derecho de la ecuación en la propiedad asociativa, vemos que X(YZ)X(YZ)X(YZ) da:

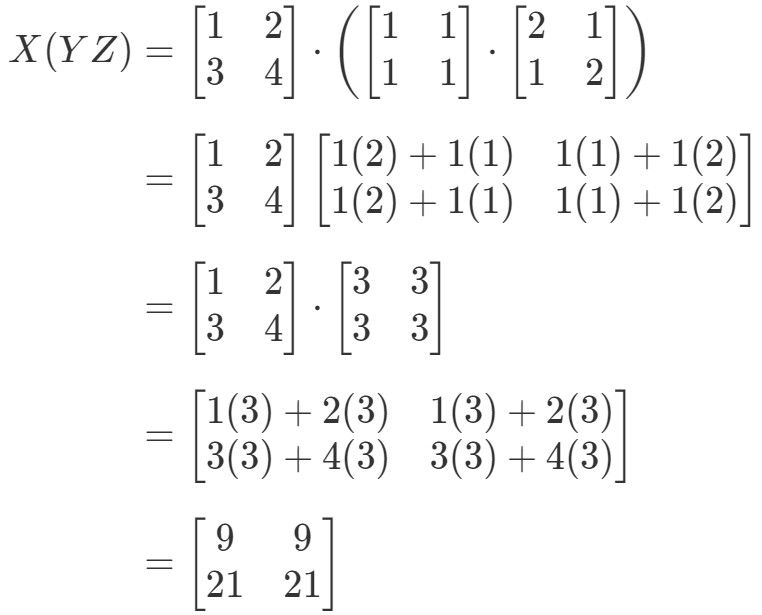
Vea cómo el lado izquierdo y el lado derecho de la ecuación son ambos iguales. Por lo tanto, ¡sabemos que la propiedad asociativa realmente funciona! ¡Una vez más, esto significa que el orden de multiplicación de la matriz no importa!

Ahora la siguiente propiedad es la propiedad distributiva. La propiedad distributiva establece que:

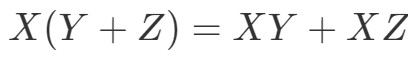
Vemos que se nos permite utilizar la técnica de la lámina para las matrices también. Para demostrar que esta propiedad funciona, hagamos un ejemplo.

Pregunta 7: Demuestra que la propiedad distributiva funciona para las siguientes matrices:

Veamos que el lado izquierdo de la ecuación es X(Y+Z)X(Y + Z)X(Y+Z). Por lo tanto, calcular eso nos da:

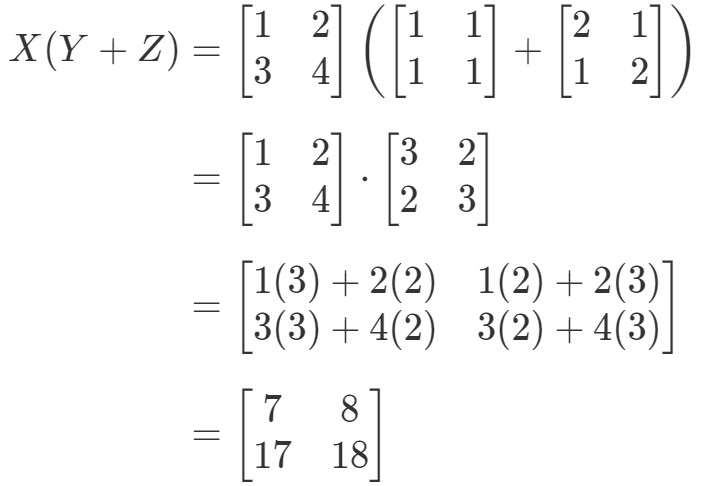
Ahora comprobemos si el lado derecho de la ecuación nos da exactamente lo mismo. Observa que el lado derecho de la ecuación es XY+XZXY + XZXY+XZ. Calculando esto nos da:

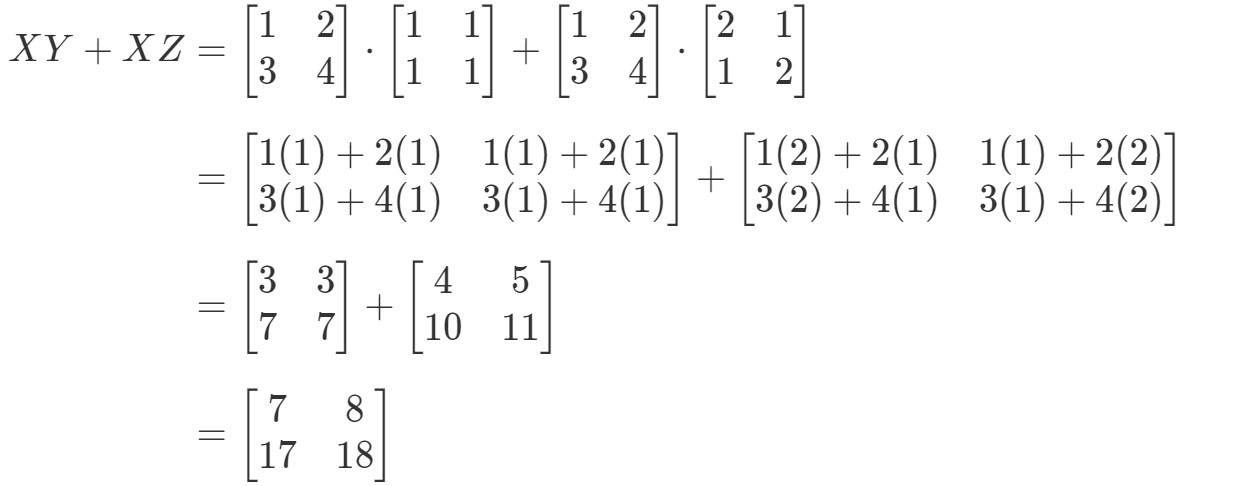
Nota que el lado izquierdo de la ecuación es exactamente el mismo que el lado derecho de la ecuación. Por lo tanto, podemos confirmar que la propiedad distributiva realmente funciona.

¿Es conmutativa la multiplicación de matrices?

Sabemos que la multiplicación de matrices satisface las propiedades asociativa y distributiva, sin embargo no hemos hablado de la propiedad conmutativa en absoluto. ¿Significa eso que la multiplicación de matrices no la satisface? En realidad no, y podemos comprobarlo con un ejemplo.

Pregunta 8: Si la multiplicación de matrices es conmutativa, entonces lo siguiente debe ser cierto:

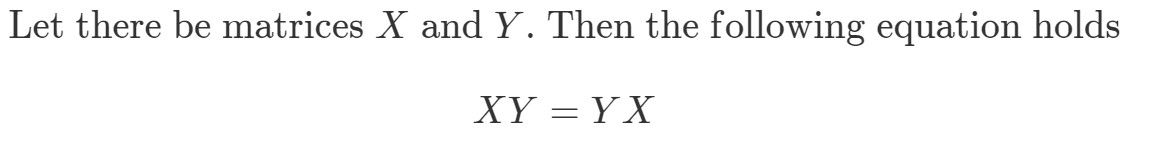
Demostrar que XYeqYXXY eq YXXYeqYX si

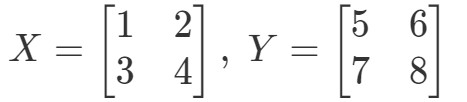
Primero calculamos el lado izquierdo de la ecuación. Calculando XYXYXY tenemos:

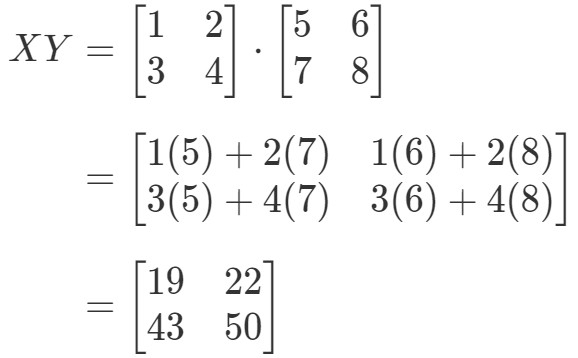
Ahora calculando el lado derecho de la ecuación, tenemos:

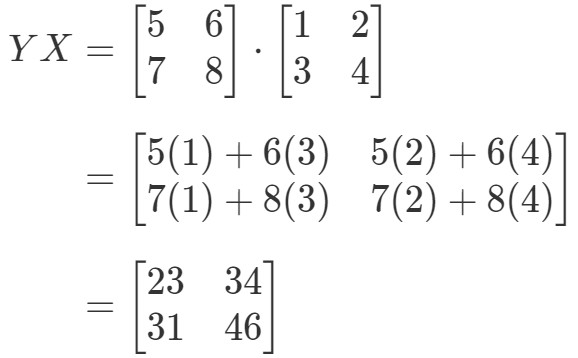
Como puedes ver,

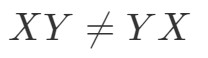
Porque tenemos

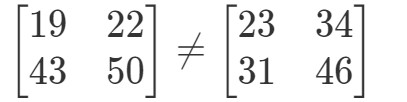
Estas dos matrices son completamente diferentes.

Ahora todavía hay algunas propiedades más de la multiplicación de matrices. Sin embargo, estas propiedades tratan de las matrices cero e identidad.

Multiplicación de matrices para la matriz cero

La propiedad de multiplicación de matrices para la matriz cero dice lo siguiente:

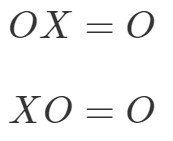
Donde OOO es una matriz cero.

Esto significa que si se multiplica una matriz cero con otra matriz distinta de cero, entonces se obtendrá una matriz cero. Comprobemos si esto es cierto con un ejemplo.

Pregunta 9: Demuestre que la ecuación OX=OOX = OOX=O y XO=OXO = OXO=O se cumple si:

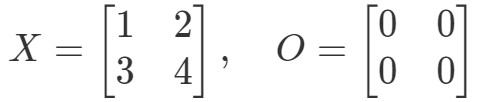
Veamos primero la ecuación

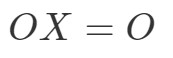
Nota que si calculamos OXOXOX nos da:

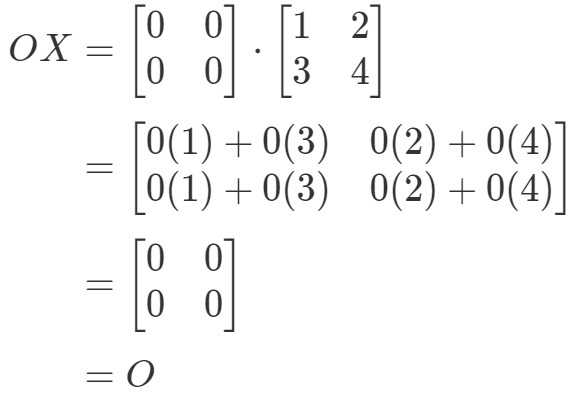
Vemos que OX=OOX = OOX=O, por lo que la ecuación se cumple. Del mismo modo, si calculamos XOXOXO, obtenemos:

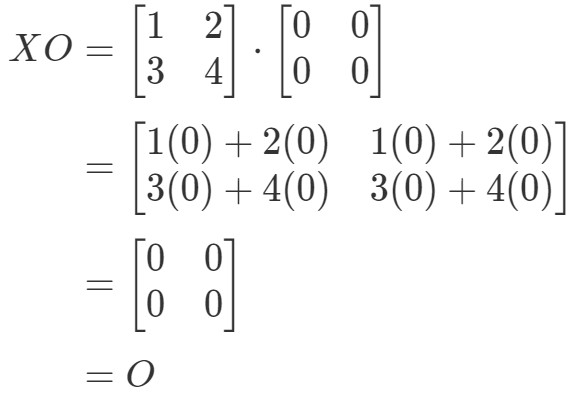
Vemos que la ecuación XO=OXO = OXO=O se cumple, así que hemos terminado.

Multiplicación matricial para la matriz identidad

¿Ahora qué pasa con la propiedad de multiplicación matricial para matrices identidad? Pues bien, la propiedad establece lo siguiente:

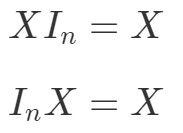
Donde InI_{n}In es una matriz identidad n×nn \N veces nn×n. De nuevo, podemos ver que las siguientes ecuaciones se cumplen con un ejemplo.

Pregunta 10: Demuestre que las ecuaciones XI2=XX I_{2} = XXI2=X e I2X=XI_{2} X = XI2X=X se cumplen con las siguientes matrices

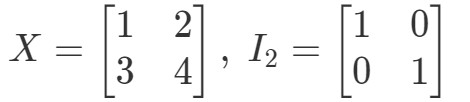
Así que para la ecuación XI2=XX I_{2} = XXI2=X, tenemos:

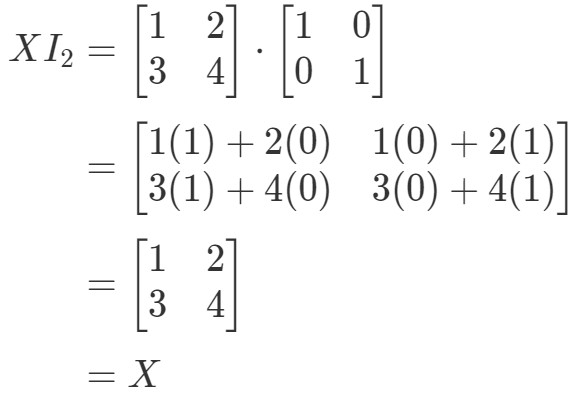
Así que la ecuación sí se cumple. De forma similar a la ecuación I2X=XI_{2}X = XI2X=X, tenemos:

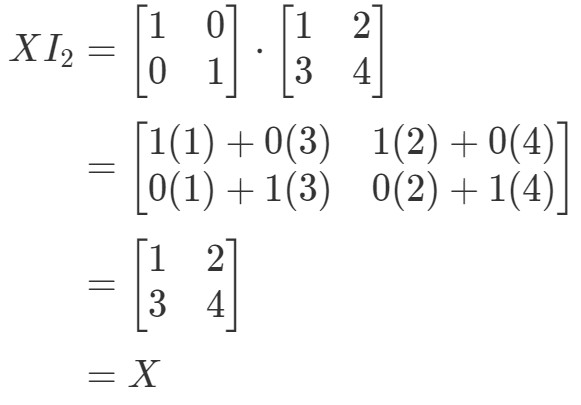
De nuevo, la ecuación se mantiene. Así que hemos terminado con la pregunta, y ambas ecuaciones se mantienen.Esto concluye todas las propiedades de la multiplicación de matrices. Ahora bien, si quieres ver una aplicación de la multiplicación de matrices en la vida real, entonces te recomiendo que veas este artículo.

https://www.mathsisfun.com/algebra/matrix-multiplying.html