Free Press

Multiplication de matrices

Il existe exactement deux façons de multiplier des matrices. La première façon est de multiplier une matrice avec un scalaire. C’est ce qu’on appelle la multiplication scalaire. La deuxième façon est de multiplier une matrice avec une autre matrice. C’est ce qu’on appelle la multiplication matricielle.

Multiplication scalaire

La multiplication scalaire est en fait une opération matricielle très simple. Pour multiplier un scalaire avec une matrice, on prend simplement le scalaire et on le multiplie à chaque entrée de la matrice. Faisons un exemple.

Question 1 : Calculez 2A2A2A si

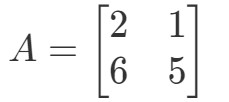
La question nous demande de trouver ce qu’est 2A2A2A. En d’autres termes, nous trouvons

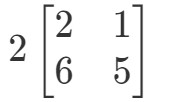
Notez que si nous devons multiplier 2 à chaque entrée de la matrice, nous obtenons que:

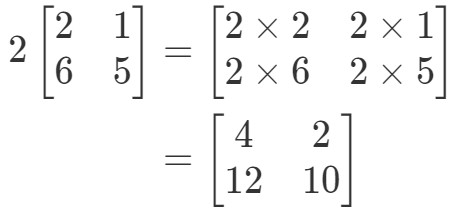
Très simple ! Faisons-en une autre.

Question 2 : calculer 0A0A0A si

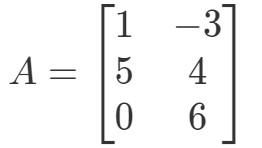
De nouveau, nous essayons de trouver 0A0A0A. Cela signifie que nous chercherons la réponse à

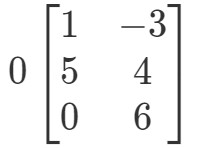
La matrice aura une forme bizarre, mais le concept reste le même. Nous allons toujours multiplier le scalaire 0 à chaque entrée de la matrice. Ce faisant, nous obtenons :

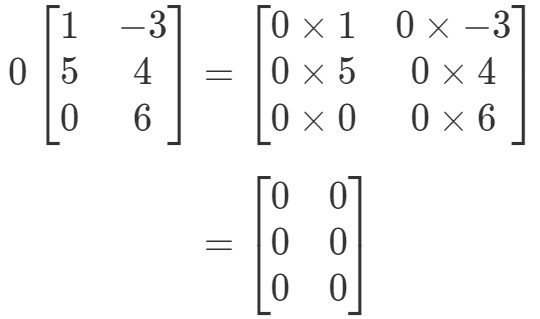
Notez que toutes les entrées de la matrice sont 0. C’est ce qu’on appelle une matrice nulle qui est 3 x 2.

Maintenant que nous sommes très familiers avec la multiplication scalaire, pourquoi ne pas passer à la multiplication matricielle ?

Comment multiplier des matrices

Pour multiplier une matrice par une autre matrice, nous devons d’abord apprendre ce qu’est le produit scalaire.

Qu’est-ce que le produit scalaire ?

Le produit scalaire (également appelé multiplication vectorielle) est une façon de calculer le produit de deux vecteurs. Par exemple, que les deux vecteurs soient :

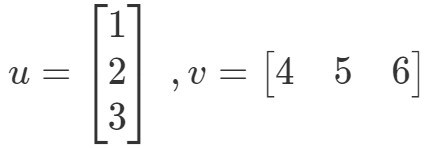
Comment pourrais-je multiplier ces deux vecteurs ? Il suffit de multiplier les entrées correspondantes, et d’ajouter les produits ensemble. En d’autres termes,

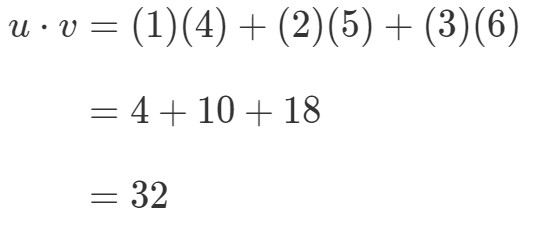
On obtient donc une seule valeur en multipliant les vecteurs. Cependant, remarquez comment que les deux vecteurs ont le même nombre d’entrées.Que faire si l’un des vecteurs a un nombre d’entrées différent de l’autre ? Par exemple, laissons

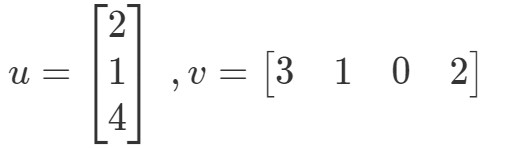
Si je devais multiplier les entrées correspondantes et les additionner toutes ensemble, alors j’obtiens :

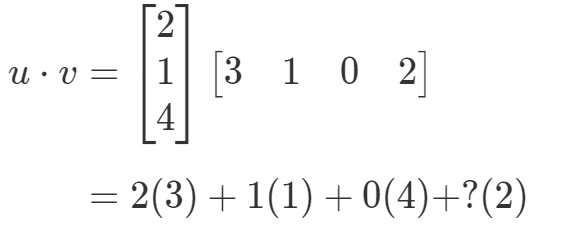
Il y a un problème ici. Les trois premières entrées ont des entrées correspondantes à multiplier avec, mais la dernière entrée ne le fait pas. Alors, que faisons-nous ici ? La réponse est que nous ne pouvons rien faire ici. Cela signifie simplement que nous ne pouvons pas calculer le produit scalaire de ces deux vecteurs.

Donc en conclusion, nous ne pouvons pas trouver le produit scalaire de deux vecteurs qui ont des nombres d’entrées différents. Ils doivent avoir le même nombre d’entrées.

Multiplication matricielle 2 x 2

Alors quel était l’intérêt d’apprendre le produit scalaire ? Eh bien, nous allons utiliser le produit scalaire lorsque nous multiplierons deux matrices ensemble. Lorsque nous multiplions une matrice avec une autre matrice, nous voulons traiter les lignes et les colonnes comme un vecteur. Plus précisément, nous voulons traiter chaque ligne de la première matrice comme des vecteurs, et chaque colonne de la deuxième matrice comme des vecteurs. Faisons un exemple.

Question 3 : Trouver A∙BA \bullet BA∙B if

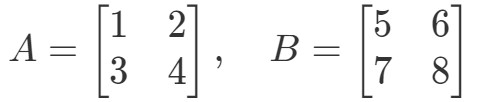
Multiplier les deux matrices nous donnera :

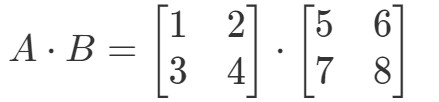
Maintenant les lignes et les colonnes sur lesquelles nous nous concentrons sont

où r1r_{1}r1 est la première ligne, r2r_{2}r2 est la deuxième ligne, et, c1,c2c_{1}, c_{2}c1,c2 sont les première et deuxième colonnes. Maintenant, nous allons traiter chaque ligne et colonne que nous voyons ici comme un vecteur.

Notez ici que la multiplication d’une matrice 2 x 2 avec une autre matrice 2 x 2 donne une matrice 2 x 2. En d’autres termes, la matrice que nous obtenons devrait avoir 4 entrées.

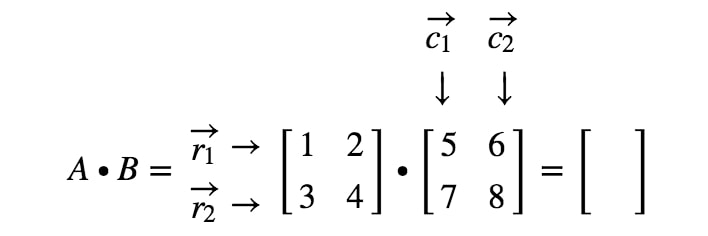
Comment obtenons-nous exactement la première entrée ? Eh bien, remarquez que la première entrée est située sur la première ligne et la première colonne. Donc nous prenons simplement le produit scalaire de r1r_{1}r1 et c1c_{1}c1. Ainsi, la première entrée sera

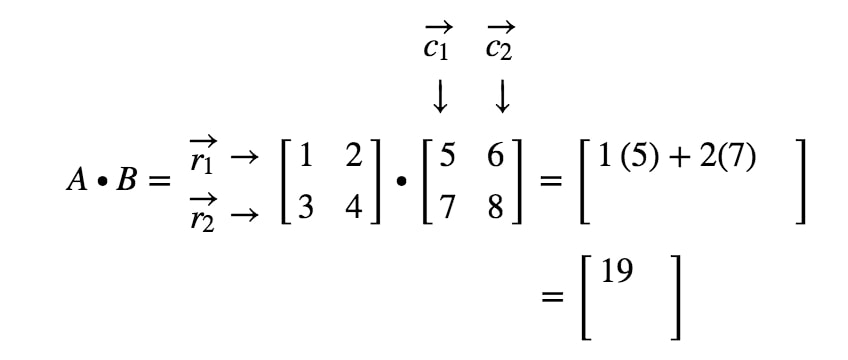
Comment obtenons-nous la deuxième entrée cette fois-ci ? Eh bien, remarquez que l’emplacement de la deuxième entrée est dans la première ligne et la deuxième colonne. Donc, nous prenons simplement le produit scalaire de r1r_{1}r1 et c2c_{2}c2. Ainsi, la deuxième entrée sera

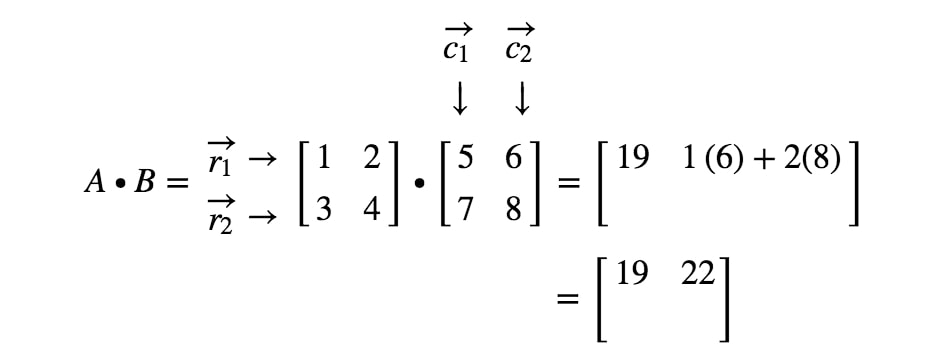
Nous allons maintenant utiliser la même stratégie pour chercher les deux dernières entrées. Remarquez que l’avant-dernière entrée est située dans la 2e2^{nd}2e ligne et la 1re^{st}1e colonne, et la dernière entrée est située dans la 2e2^{nd}2e ligne et la 2e2^{nd}2e colonne. On prend donc le produit scalaire de r2r_{2}r2 et c1c_{1}c1, et le produit scalaire de r2r_{2}r2 et c2c_{2}c2. Cela nous donne:

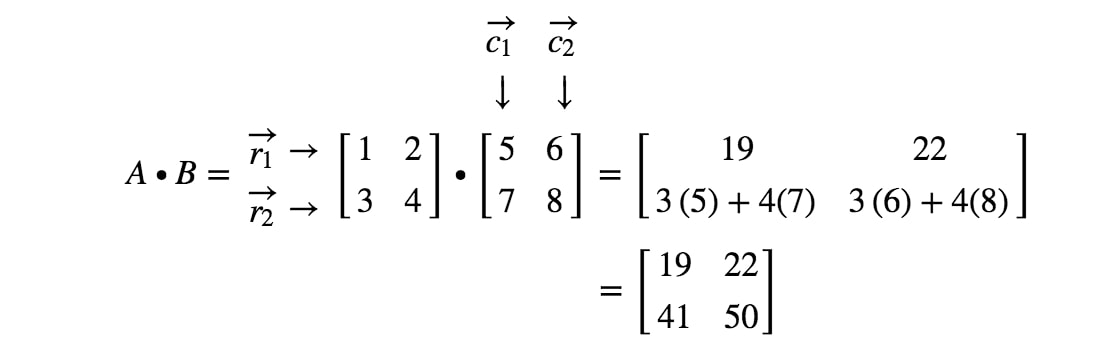
Maintenant nous avons terminé ! Voici ce que nous obtenons lorsque nous multiplions des matrices 2 x 2. En général, la formule de multiplication matricielle pour les matrices 2 x 2 est

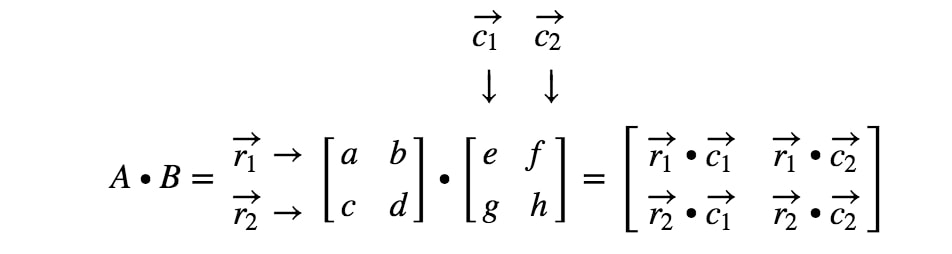
Multiplication matricielle 3 x 3

Maintenant, le processus de multiplication matricielle 3 x 3 est très similaire au processus de multiplication matricielle 2 x 2. Encore une fois, pourquoi ne pas faire un exemple de multiplication matricielle ?

Question 4:Trouver A∙BA \bullet BA∙B if

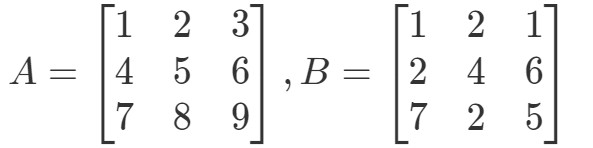
Premièrement, remarquez que les multiplier devrait nous donner une autre matrice 3 x 3. En d’autres termes,

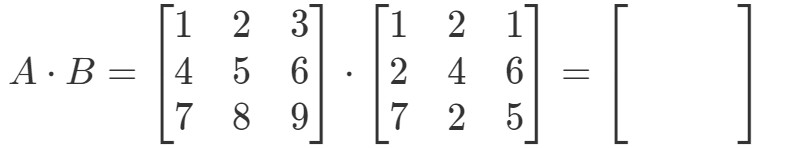
Maintenant, étiquetons toutes nos lignes dans la première matrice et nos colonnes dans la deuxième matrice.

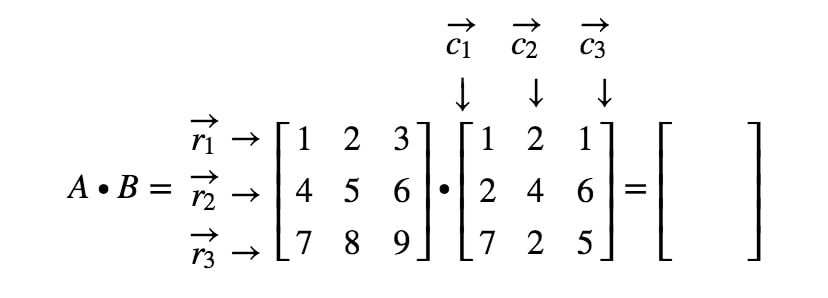
Notez que la première entrée de la matrice est située dans la 1ère1^{st}1ère ligne et la 1ère1^{st}1ère colonne, nous prenons donc le produit scalaire de r1r_{1}r1 et c1c_{1}c1. Cela nous donne :

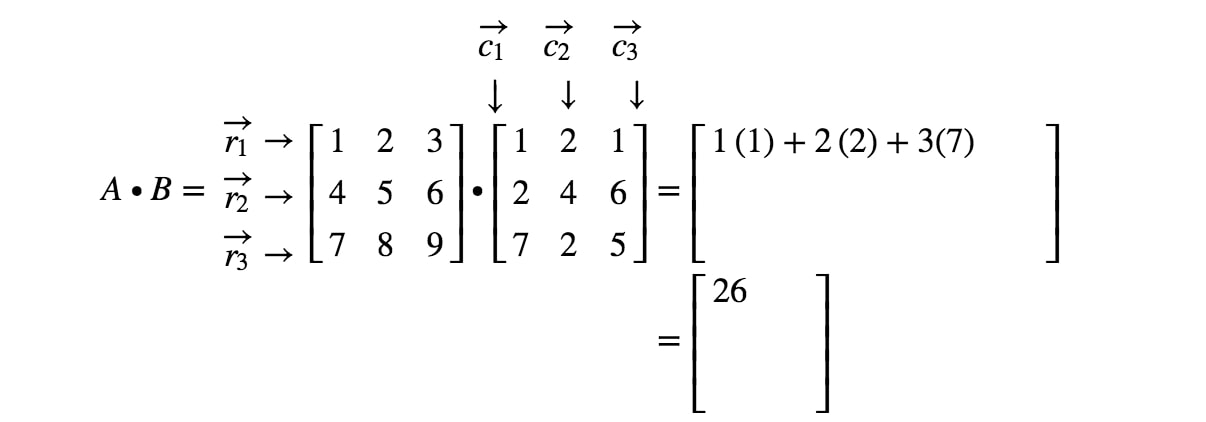
Nous remarquons maintenant que la deuxième entrée de la matrice est située dans la 1ère1^{st}1ère ligne et la 2ème2^{nd}2ème colonne. Ainsi, nous prenons le produit scalaire de r1r_{1}r1 et c2c_{2}c2. Cela nous donne :

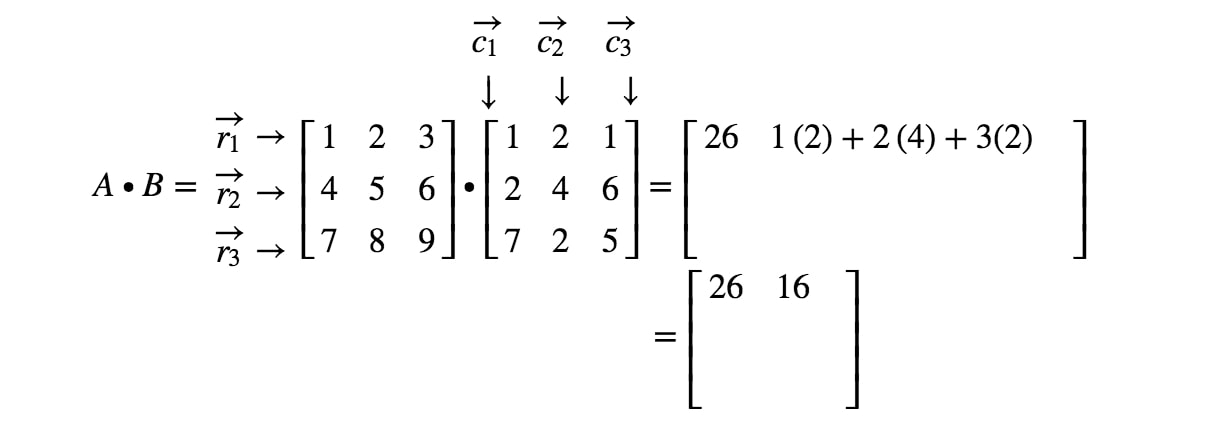
Si nous devons continuer à localiser toutes les entrées et faire le produit scalaire correspondant aux lignes et aux colonnes, alors nous obtenons le résultat final.

Nous avons terminé ! Remarquez que plus les matrices sont grandes, plus la multiplication matricielle devient fastidieuse. C’est parce que nous devons traiter de plus en plus de nombres ! En général, la formule de multiplication matricielle pour les matrices 3 x 3 est

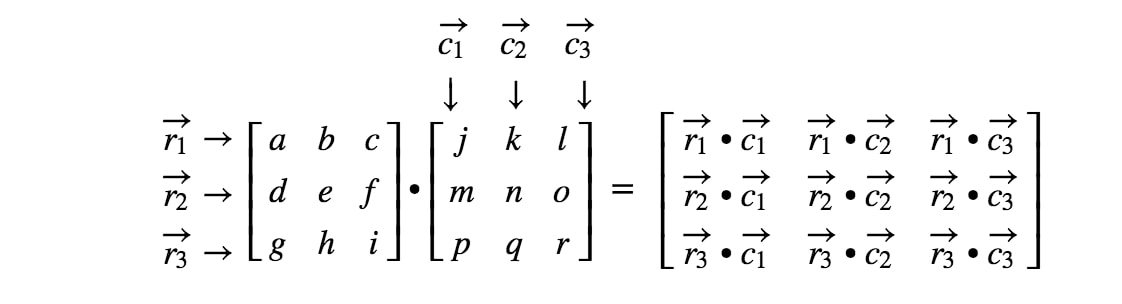
Comment multiplier des matrices avec des dimensions différentes?

Jusqu’à présent, nous avons multiplié des matrices avec les mêmes dimensions. De plus, nous savons que la multiplication de deux matrices de même dimension donne une matrice de même dimension. Mais que se passe-t-il si nous multiplions une matrice avec des dimensions différentes ? Comment pouvons-nous connaître les dimensions de la matrice calculée ? D’abord, nous devons voir que la multiplication des matrices vous donne une matrice définie.

La matrice est-elle définie?

Il y a des cas où il n’est pas possible de multiplier deux matrices ensemble. Pour ces cas, on dit que la matrice est indéfinie. Comment savoir si elles sont indéfinies ?

Le produit de deux matrices n’est défini que si le nombre de colonnes de la première matrice est égal au nombre de lignes de la seconde.

Essayons d’utiliser cette définition dans cet exemple.

Question 5 : Soit

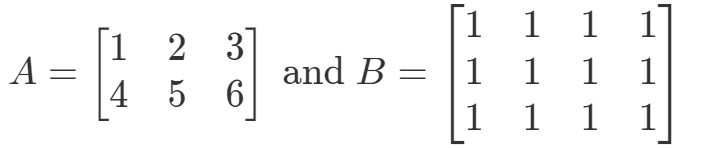
Est-ce que A∙BA \bullet BA∙B est défini?

Premièrement, remarquez que la première matrice a 3 colonnes. De même, la deuxième matrice a 3 lignes. Puisqu’elles sont toutes deux égales à 3, alors je sais que A∙BA \bullet BA∙B est défini.

Maintenant que nous savons qu’il est défini, comment connaîtrions-nous les dimensions de A∙BA \bullet BA∙B ?

La propriété de dimension

Pour trouver les dimensions de A∙BA \bullet BA∙B, nous devons d’abord regarder les dimensions de et séparément.

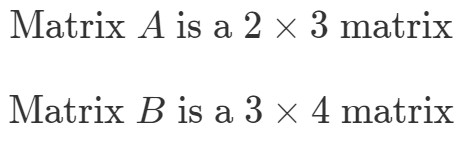
Nous allons maintenant mettre les dimensions des matrices côte à côte comme ceci:

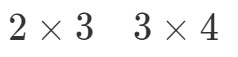
Ce que nous allons faire maintenant, c’est prendre le premier nombre et le dernier nombre et les combiner pour obtenir les dimensions de A∙BA \bullet BA∙B. Vous voyez que le premier nombre est 2 et le dernier est 4. Donc les dimensions de A∙BA \bullet BA∙B seront:

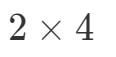
Maintenant que nous connaissons les dimensions de la matrice, nous pouvons juste calculer chaque entrée en utilisant les produits scalaires. Cela nous donnera :

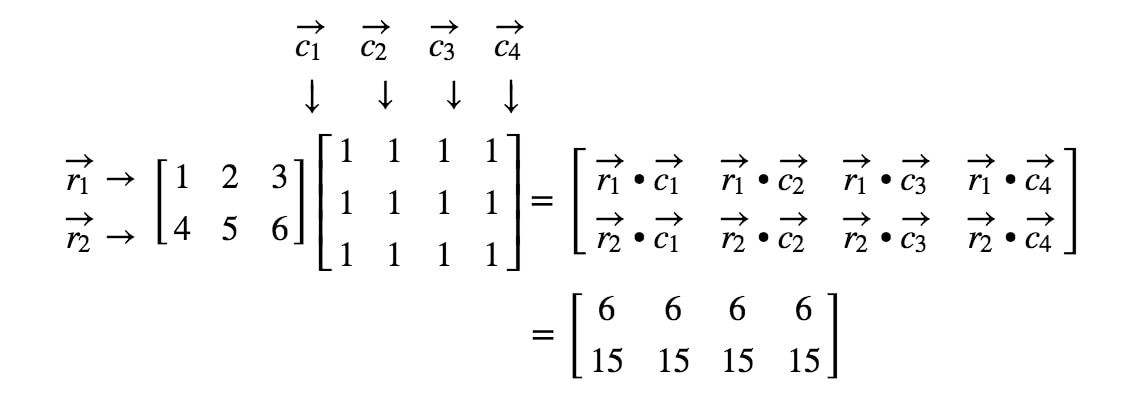
Maintenant que nous savons très bien comment multiplier des matrices, pourquoi ne pas jeter un coup d’œil à quelques règles de multiplication matricielle ?

Propriétés de la multiplication matricielle

Alors, quel type de propriétés la multiplication matricielle possède-t-elle réellement ? Tout d’abord, définissons tout formellement.

Disons que X, Y, ZX, Y, ZX, Y, Z sont des matrices, InI_{n}In est une matrice d’identité, et OnO_{n}On est une matrice nulle. Si ces cinq matrices ont toutes des dimensions égales, alors nous aurons les propriétés de multiplication de matrice à matrice suivantes :

La propriété associative stipule que l’ordre dans lequel vous multipliez n’a pas d’importance. En d’autres termes, calculer X∙YX \bullet YX∙Y puis multiplier avec ZZZ vous donnerait le même résultat que calculer Y∙ZY \bullet ZY∙Z puis multiplier avec XXX. Faisons un exemple.

Question 6 : Montrez que la propriété associative fonctionne avec ces matrices :

En regardant le côté gauche de l’équation de la propriété associative, nous voyons que (XY)Z(XY)Z(XY)Z donne :

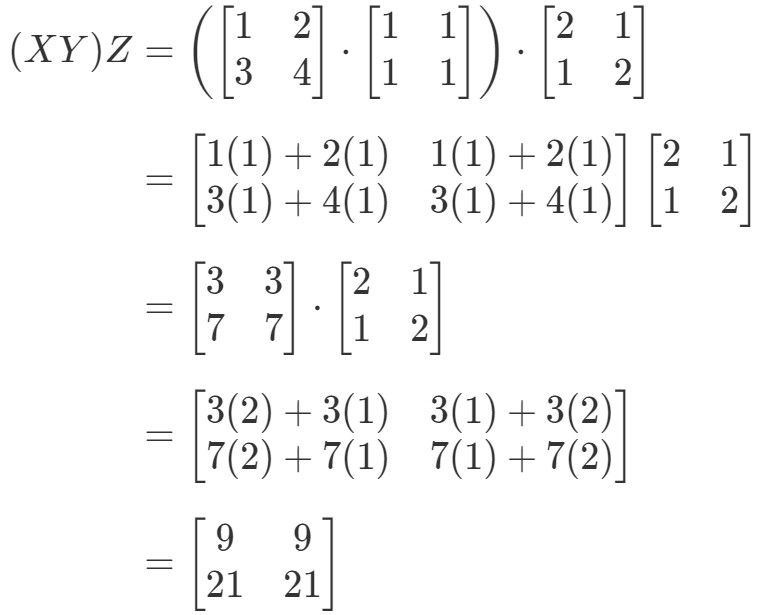
En regardant maintenant le côté droit de l’équation de la propriété associative, nous voyons que X(YZ)X(YZ)X(YZ) donne:

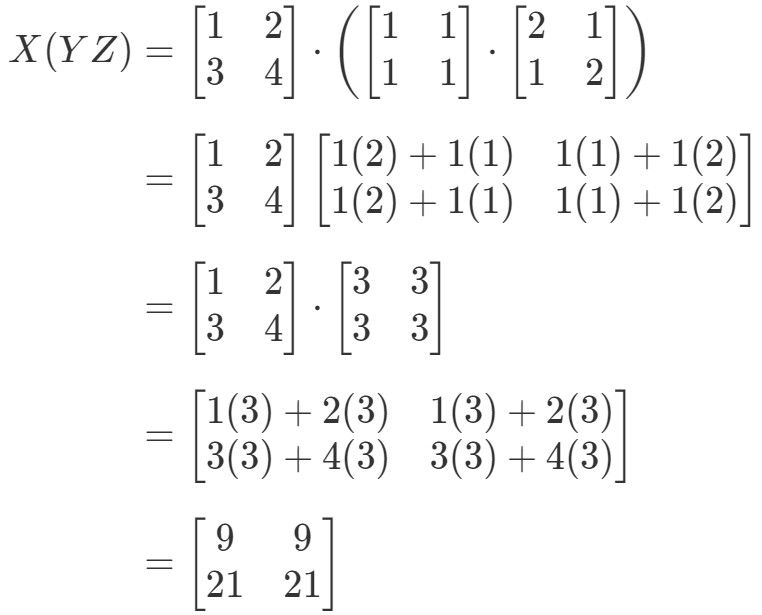
Voyez comment le côté gauche et le côté droit de l’équation sont tous deux égaux. Par conséquent, nous savons que la propriété associative fonctionne réellement ! Encore une fois, cela signifie que l’ordre de multiplication de la matrice n’a pas d’importance !

Maintenant la propriété suivante est la propriété distributive. La propriété distributive stipule que :

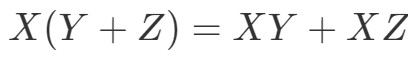
Nous voyons que nous sommes autorisés à utiliser la technique du fleuret pour les matrices également. Juste pour montrer que cette propriété fonctionne, faisons un exemple.

Question 7 : Montrez que la propriété distributive fonctionne pour les matrices suivantes :

Voyez que le côté gauche de l’équation est X(Y+Z)X(Y + Z)X(Y+Z). Par conséquent, calculer cela nous donne :

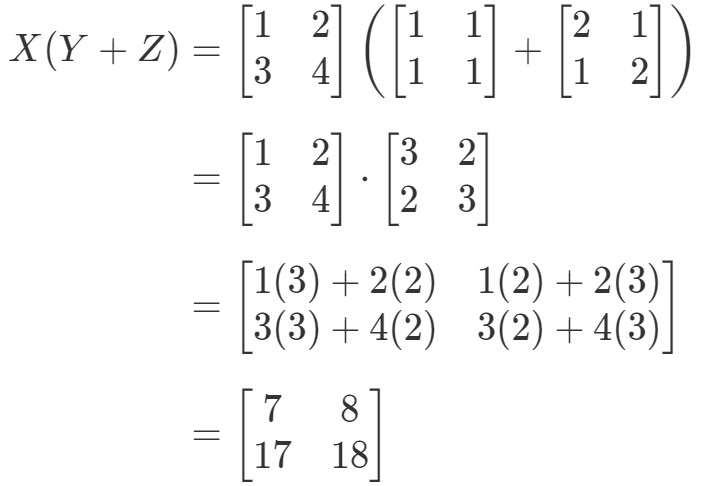
Vérifions maintenant si le côté droit de l’équation nous donne exactement la même chose. Remarquez que le côté droit de l’équation est XY+XZXY + XZXY+XZ. En calculant cela, on obtient:

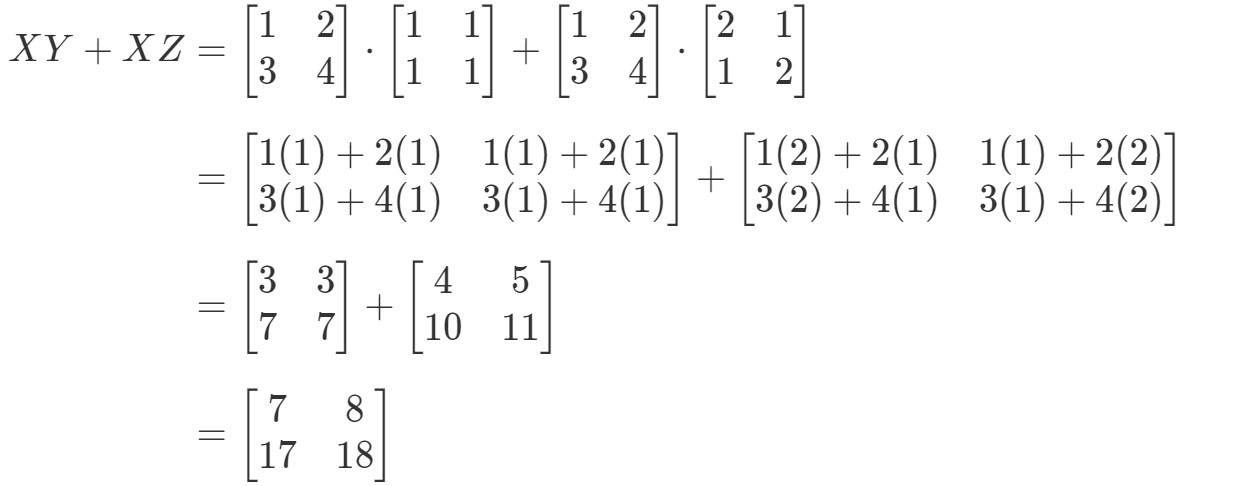
Notez que le côté gauche de l’équation est exactement le même que le côté droit de l’équation. Par conséquent, nous pouvons confirmer que la propriété distributive fonctionne réellement.

La multiplication matricielle est-elle commutative ?

Nous savons que la multiplication matricielle satisfait les propriétés associative et distributive, cependant nous n’avons pas du tout parlé de la propriété commutative. Cela signifie-t-il que la multiplication matricielle ne la satisfait pas ? En fait non, et nous pouvons le vérifier avec un exemple.

Question 8 : Si la multiplication matricielle est commutative, alors ce qui suit doit être vrai :

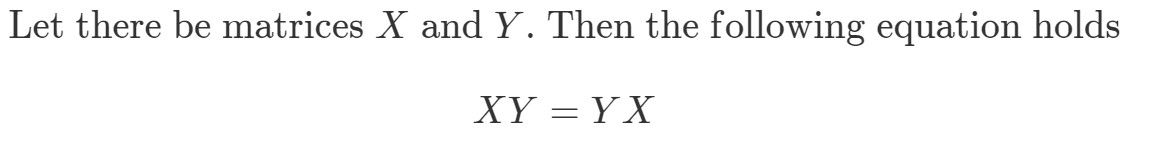
Montrez que XYeqYXXY eq YXXYeqYX si

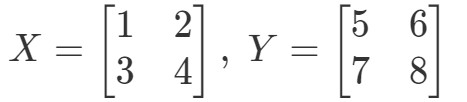
D’abord on calcule le côté gauche de l’équation. En calculant XYXYXY, on obtient:

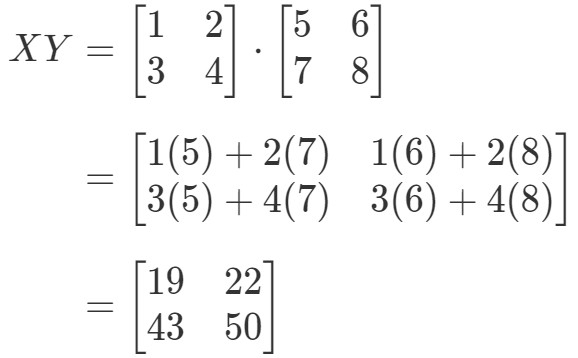
En calculant maintenant le côté droit de l’équation, on a:

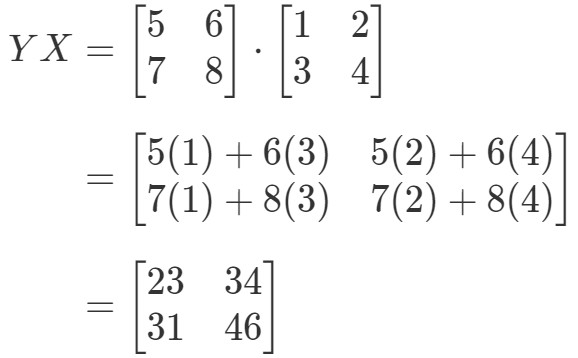
Comme vous pouvez le voir,

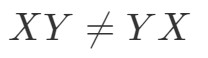
Parce que nous avons

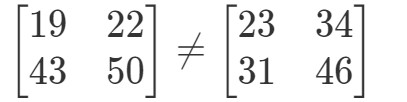
Ces deux matrices sont complètement différentes.

Maintenant il reste encore quelques propriétés de la multiplication des matrices. Cependant, ces propriétés traitent des matrices zéro et identité.

Multiplication des matrices pour la matrice zéro

La propriété de multiplication des matrices pour la matrice zéro énonce ce qui suit :

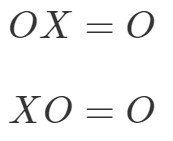
où OOO est une matrice zéro.

Cela signifie que si vous deviez multiplier une matrice nulle avec une autre matrice non nulle, alors vous obtiendrez une matrice nulle. Testons si cela est vrai avec un exemple.

Question 9 : Montrez que l’équation OX=OOX = OOX=O et XO=OXO = OXO=O tient si :

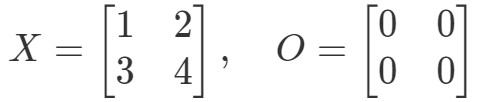
Regardons d’abord l’équation

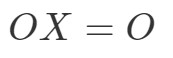
Notez que le calcul de OXOXOX nous donne :

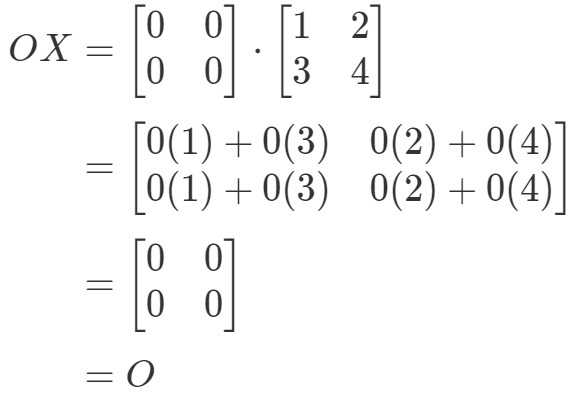
Nous voyons bien que OX=OOX = OOX=O, donc l’équation tient. De même, si nous calculons XOXOXO, nous obtenons :

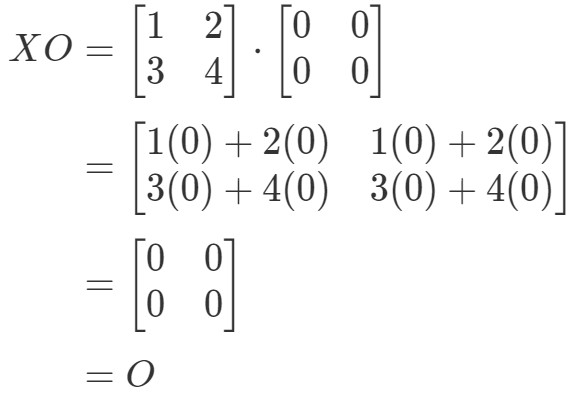
Nous voyons bien que l’équation XO=OXO = OXO=O tient, donc nous avons terminé.

Multiplication matricielle pour la matrice d’identité

Mais qu’en est-il de la propriété de multiplication matricielle pour les matrices d’identité ? Eh bien, cette propriété énonce ce qui suit :

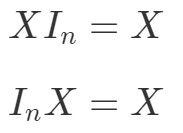
où InI_{n}In est une matrice d’identité n×nn \times nn×n. Encore une fois, on peut voir que les équations suivantes tiennent bien avec un exemple.

Question 10 : Montrez que les équations XI2=XX I_{2} = XXI2=X et I2X=XI_{2}. X = XI2X=X tiennent avec les matrices suivantes

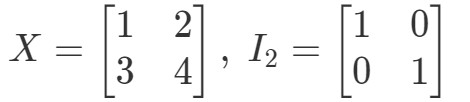
Donc pour l’équation XI2=XX I_{2} = XXI2=X, on a :

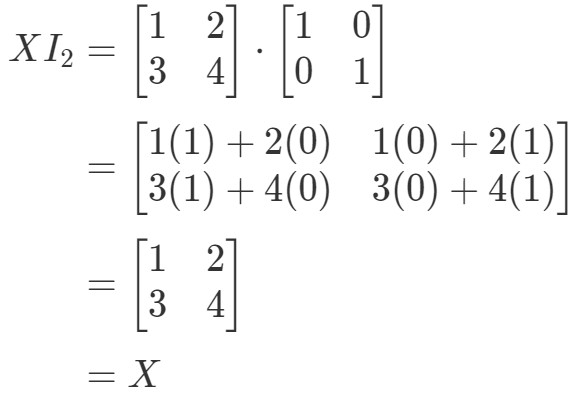
Donc l’équation tient bien. Semblable à l’équation I2X=XI_{2}X = XI2X=X, nous avons:

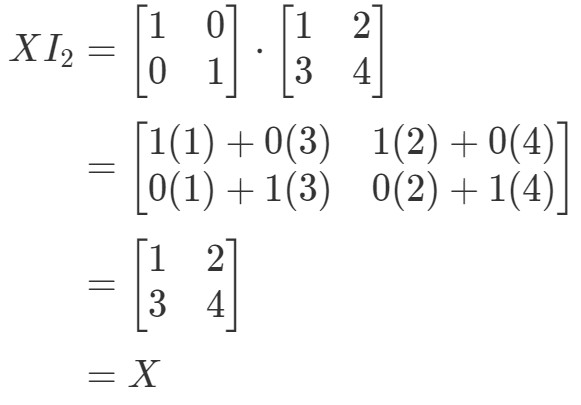
De nouveau, l’équation tient. Donc, nous avons terminé avec la question, et les deux équations tiennent.Ceci conclut toutes les propriétés de la multiplication matricielle. Maintenant, si vous voulez regarder une application réelle de la multiplication matricielle, alors je vous recommande de regarder cet article.

https://www.mathsisfun.com/algebra/matrix-multiplying.html