Free Press

Matrix Multiplication

Há exatamente duas maneiras de multiplicar matrizes. A primeira maneira é multiplicar uma matriz com uma escalar. Isto é conhecido como multiplicação escalar. A segunda maneira é multiplicar uma matriz com outra matriz. Isto é conhecido como multiplicação de matriz.

Scalar Multiplicação

multiplicação escalar é na verdade uma operação muito simples de matriz. Para multiplicar uma escalar com uma matriz, nós simplesmente pegamos a escalar e a multiplicamos para cada entrada na matriz. Vamos fazer um exemplo.

Questão 1: Calcular 2A2A2A se

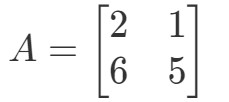
A pergunta é para descobrir o que é 2A2A2A. Em outras palavras, estamos encontrando

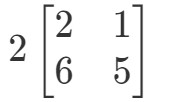
Note que se formos multiplicar 2 a cada entrada na matriz, obtemos que:

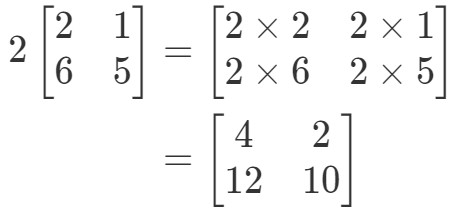
Muito simples! Vamos fazer outra.

Questão 2: Calcular 0A0A0A se

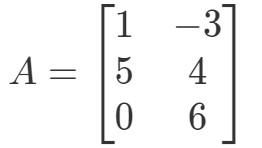
Ganhar, estamos tentando encontrar 0A0A0A. Isto significa que estaremos procurando a resposta para

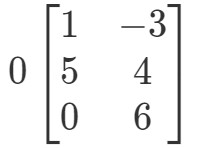
A matriz terá uma forma estranha, mas o conceito permanece o mesmo. Nós ainda vamos multiplicar o escalar 0 para cada entrada na matriz. Fazendo isso nos dá:

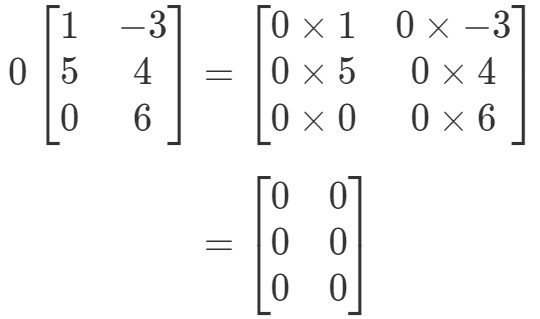
Note que todas as entradas na matriz são 0. Isto é conhecido como uma matriz zero que é 3 x 2.

Agora que estamos muito familiarizados com a multiplicação escalar, porque não passamos para a multiplicação matricial?

Como Multiplicar Matrizes

Para multiplicar uma matriz por outra matriz, precisamos primeiro aprender o que é produto de ponto.

O que é produto de ponto?

Produto de ponto (também conhecido como multiplicação vetorial) é uma forma de calcular o produto de dois vetores. Por exemplo, deixe os dois vectores ser:

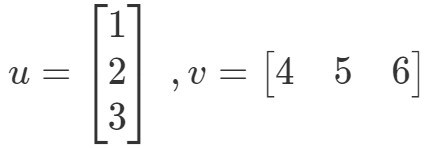
Como multiplicaria estes dois vectores? Simplesmente multiplique as entradas correspondentes e adicione os produtos juntos. Em outras palavras,

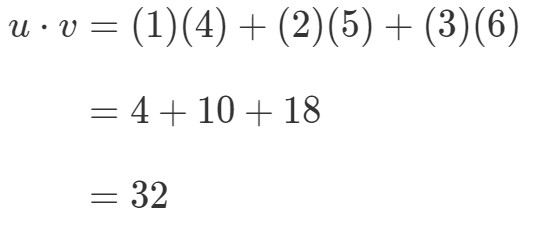
Então obtemos um único valor multiplicando os vetores. No entanto, observe como os dois vetores têm o mesmo número de entradas. E se um dos vetores tiver um número de entradas diferente do outro? Por exemplo, let

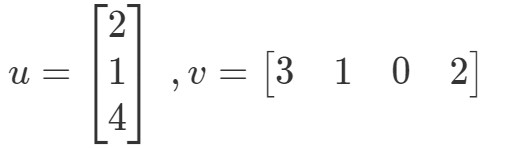
Se eu fosse multiplicar as entradas correspondentes e somá-las todas, então eu teria:

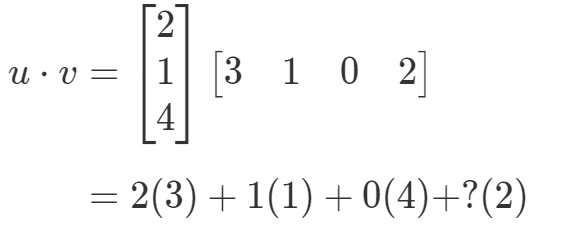
Exemplo de Falha de Produto Ponto pt.2

Há aqui um problema. As três primeiras entradas têm entradas correspondentes para multiplicar, mas a última entrada não tem. Então o que é que fazemos aqui? A resposta é que não podemos fazer nada aqui. Isto apenas significa que não podemos calcular o produto de pontos destes dois vectores.

Então, em conclusão, não podemos encontrar o produto de pontos de dois vectores que têm números de entradas diferentes. Eles devem ter o mesmo número de entradas.

2 x 2 Matrix Multiplication

Então, qual foi o objectivo de aprender o produto de pontos? Bem, estaremos usando o produto ponto quando multiplicarmos duas matrizes juntas. Ao multiplicar uma matriz com outra matriz, queremos tratar as linhas e colunas como um vetor. Mais especificamente, queremos tratar cada linha na primeira matriz como vetores, e cada coluna na segunda matriz como vetores. Vamos fazer um exemplo.

Questão 3: Encontrar A∙BA \bullet BA∙B if

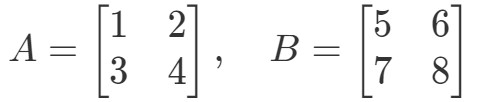
Multiplicar as duas matrizes nos dará:

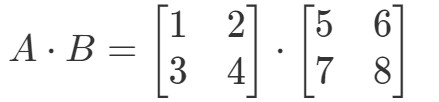
Agora as linhas e as colunas que estamos focando são

onde r1r_{1}r1 é a primeira linha, r2r_{2}r2 é a segunda linha, e, c1,c2c_{1}, c_{2}c1,c2 são a primeira e segunda colunas. Agora vamos tratar cada linha e coluna que vemos aqui como um vector.

Notificação aqui que multiplicar uma matriz 2 x 2 com outra matriz 2 x 2 dá uma matriz 2 x 2. Em outras palavras, a matriz que obtemos deve ter 4 entradas.

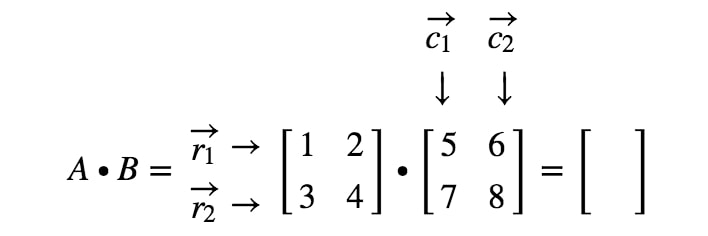
Como obtemos exatamente a primeira entrada? Bem, note que a primeira entrada está localizada na primeira linha e primeira coluna. Então nós simplesmente pegamos o produto ponto de r1r_{1}r1 e c1c_{1}c1. Assim, a primeira entrada será

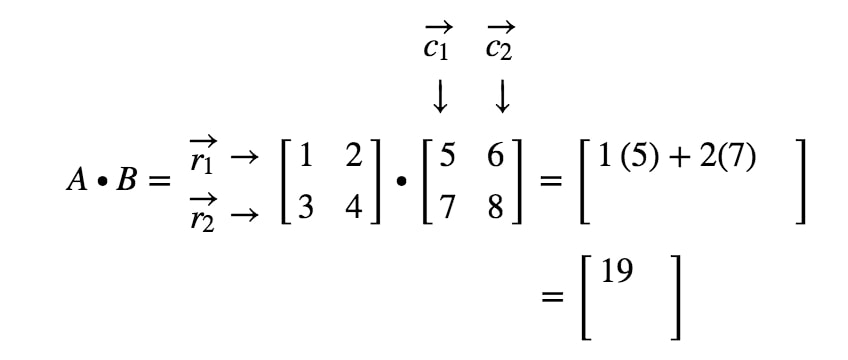
Como obtemos a segunda entrada desta vez? Bem, note que a localização da segunda entrada é na primeira linha e na segunda coluna. Então simplesmente pegamos o produto ponto de r1r_{1}r1 e c2c_{2}c2. Assim, a segunda entrada será

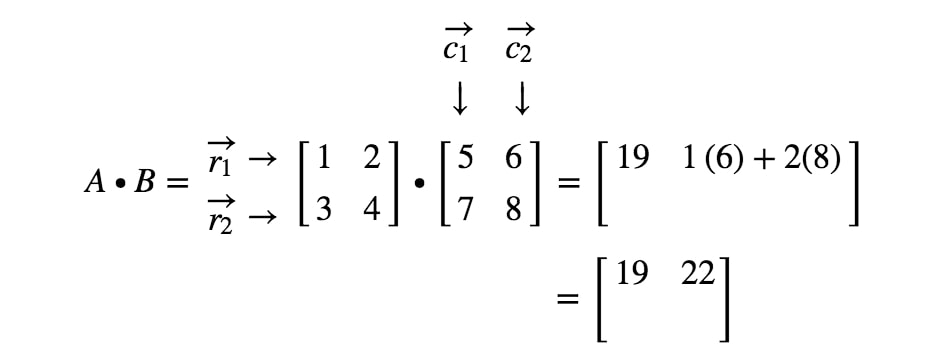
Agora vamos usar a mesma estratégia para procurar as duas últimas entradas. Note que a segunda última entrada está localizada na 2ª2^{nd}2ª linha e 1ª1^{st}1ª coluna, e a última entrada está localizada na 2ª2^{nd}2ª linha e 2ª2^{nd}2ª coluna. Então pegamos o produto ponto de r2r_{2}r2 e c1c_{1}c1, e o produto ponto de r2r_{2}r2 e c2c_{2}c2. Isto nos dá:

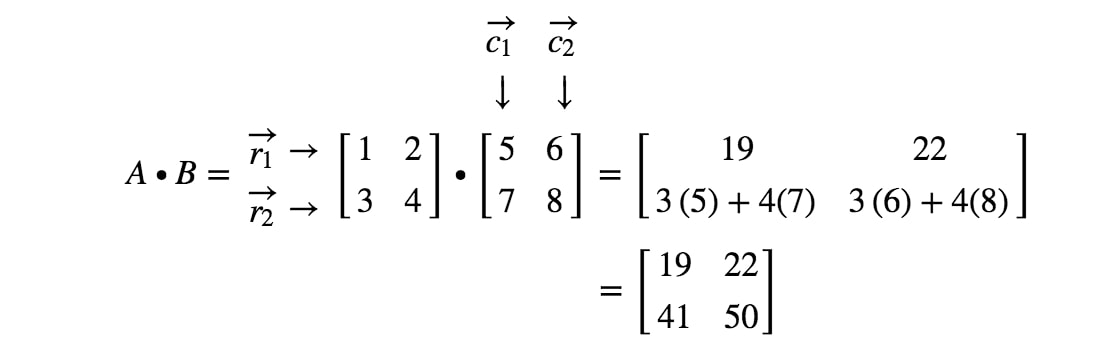
Agora estamos prontos! Isto é o que obtemos quando estamos a multiplicar 2 x 2 matrizes. Em geral, a fórmula da multiplicação matricial para 2 x 2 matrizes é

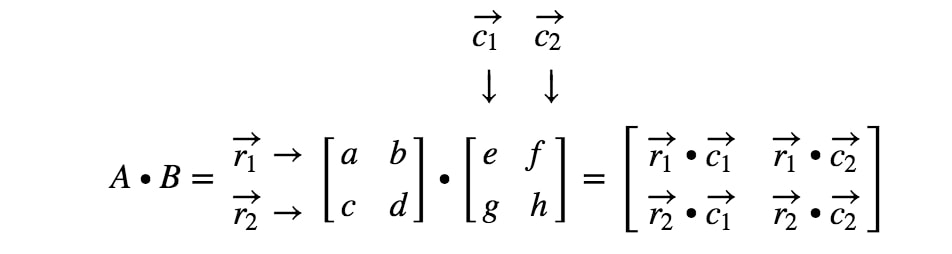
3×3 Matrix Multiplication

Agora o processo de uma multiplicação matricial 3 x 3 é muito semelhante ao processo de uma multiplicação matricial 2 x 2. Novamente, porque não fazemos um exemplo de multiplicação matricial?

Question 4:Find A∙BA \bullet BA∙B if

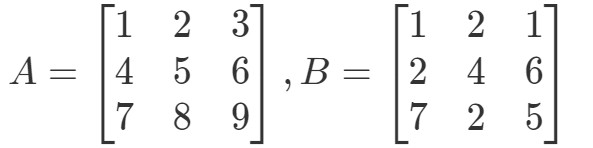
Primeiro, repare que multiplicá-las deve dar-nos outra matriz 3 x 3. Em outras palavras,

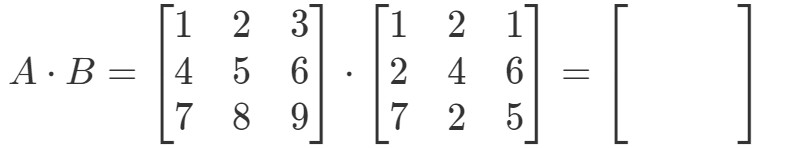
Agora vamos etiquetar todas as nossas linhas na primeira matriz e colunas na segunda matriz.

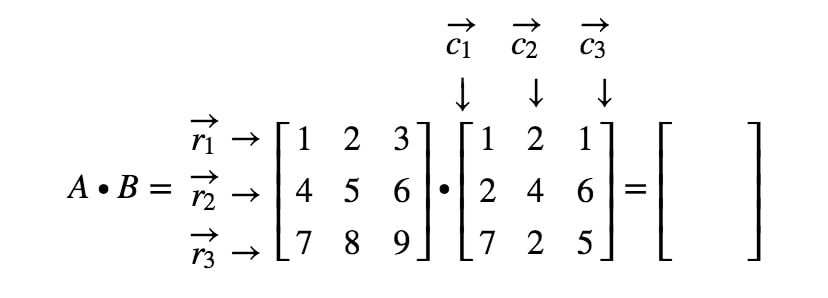
Note que a primeira entrada da matriz está localizada na 1ª1^{st}1ª linha e 1ª1^{st}1ª coluna, então pegamos o produto de pontos de r1r_{1}r1 e c1c_{1}c1. Isto nos dá:

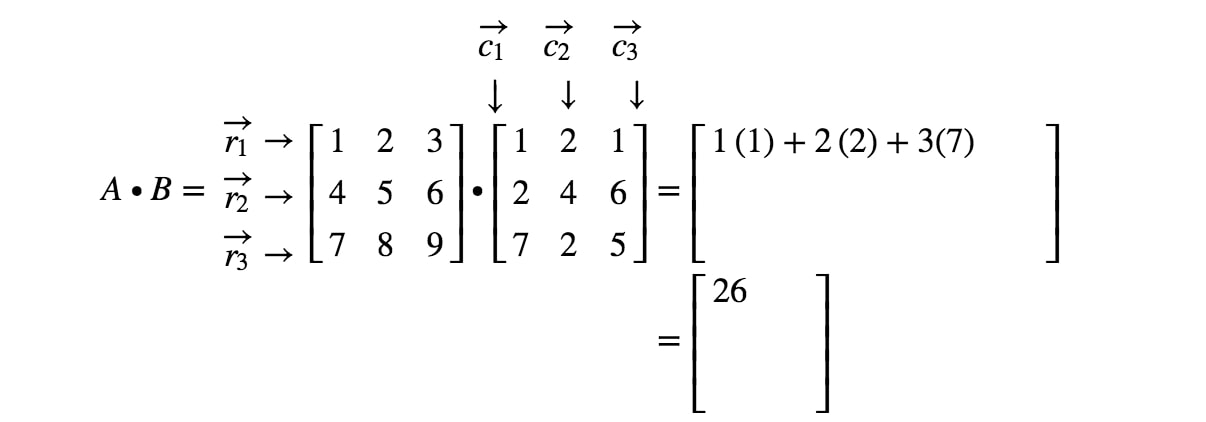
Agora note que a segunda entrada da matriz está localizada na 1ª1^{st}1ª fila e 2ª2^{nd}2ª coluna. Assim, tomamos o produto ponto de r1r_{1}r1 e c2c_{2}c2. Isto dá-nos:

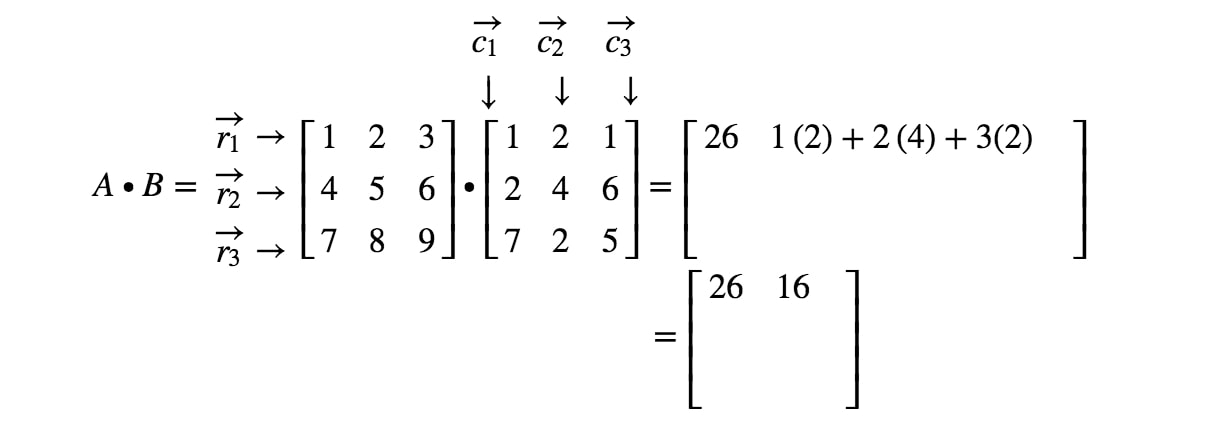
Se quisermos continuar localizando todas as entradas e fazendo o produto de pontos correspondentes às linhas e colunas, então teremos o resultado final.

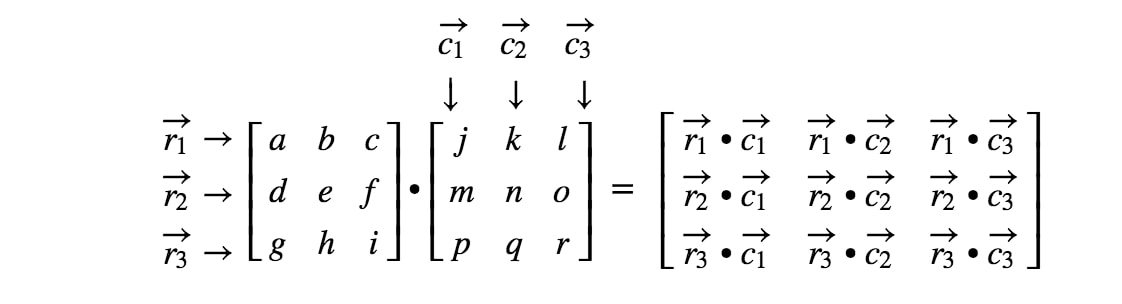
Estamos prontos! Note que quanto maiores forem as matrizes, mais tediosa se torna a multiplicação matricial. Isto é porque temos que lidar com cada vez mais números! Em geral, a fórmula de multiplicação de matrizes para 3 x 3 matrizes é

Como Multiplicar Matrizes com Dimensões Diferentes?

Até agora temos multiplicado matrizes com as mesmas dimensões. Além disso, sabemos que a multiplicação de duas matrizes com a mesma dimensão dá uma matriz com as mesmas dimensões. Mas o que acontece se multiplicarmos uma matriz com dimensões diferentes? Como saberíamos as dimensões da matriz computada? Primeiro, precisamos ver multiplicar as matrizes dá uma matriz definida.

É a Matriz Definida?

Existem casos em que não é possível multiplicar duas matrizes juntas. Para esses casos, chamamos a matriz de ser indefinida. Como podemos dizer se são indefinidas?

O produto de duas matrizes só é definido se o número de colunas na primeira matriz for igual ao número de linhas da segunda matriz.

Tentemos usar esta definição neste exemplo.

Questão 5: Let

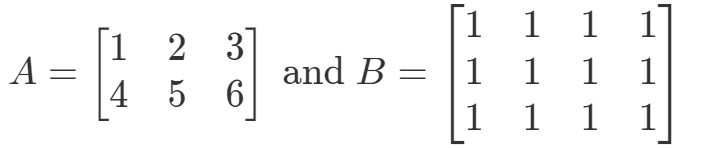
Is A∙BA \bullet BA∙B definido?

Primeiro, note que a primeira matriz tem 3 colunas. Além disso, a segunda matriz tem 3 filas. Como ambas são iguais a 3, então eu sei que A∙BA \bullet BA∙B está definido.

Agora sabemos que está definido, como saberíamos as dimensões de A∙BA \bullet BA∙B?

A Propriedade da Dimensão

Para encontrar as dimensões de A∙BA \bullet BA∙B, precisamos primeiro olhar para as dimensões de e separadamente.

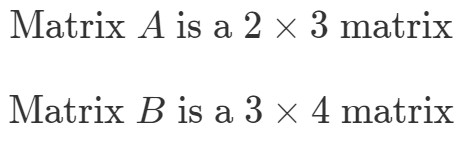
Agora vamos colocar as dimensões das matrizes lado a lado assim:

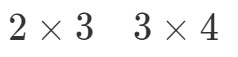
O que vamos fazer agora é pegar o primeiro número e o último número e combiná-lo para obter as dimensões de A∙BA \bullet BA∙B. Veja que o primeiro número é 2 e o último número é 4. Então as dimensões da A∙BA \bullet BA∙B serão:

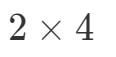
Agora que sabemos as dimensões da matriz, podemos apenas calcular cada entrada usando os produtos ponto. Isto nos dará:

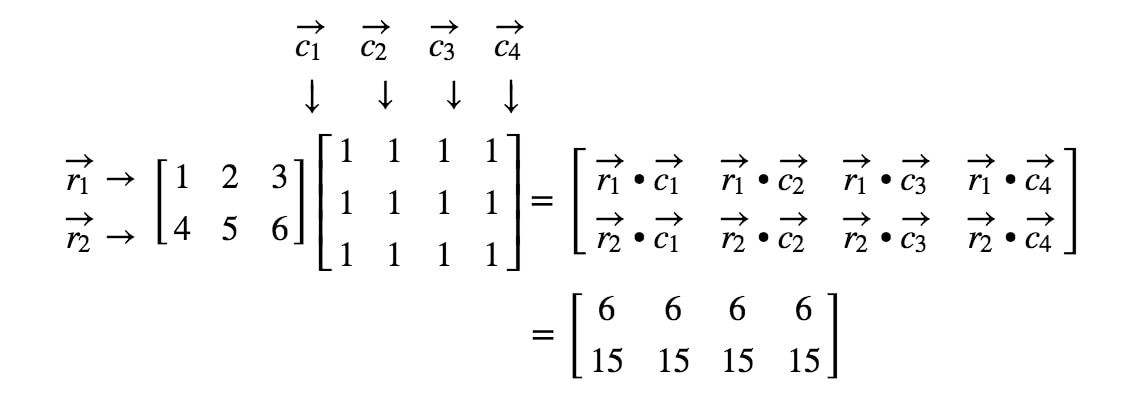
Agora que sabemos como multiplicar matrizes muito bem, por que não dar uma olhada em algumas regras de multiplicação de matrizes?

Propriedades de multiplicação de matrizes

Então que tipo de propriedades a multiplicação de matrizes realmente tem? Primeiro, vamos definir formalmente tudo.

Let X,Y,ZX, Y, ZX,Y,Z sejam matrizes, InI_{n}In be an identity matrix, e OnO_{n}On be a zero matrix. Se todas estas cinco matrizes tiverem dimensões iguais, então teremos as seguintes propriedades de multiplicação matriz a matriz:

A propriedade associativa afirma que a ordem em que se multiplica não importa. Por outras palavras, calcular X∙YX \bullet YX∙Y e depois multiplicar com ZZZ dar-lhe-ia o mesmo resultado que calcular Y∙ZY \bullet ZY∙Z e depois multiplicar com XXX. Vamos fazer um exemplo.

Questão 6: Mostre que a propriedade associativa funciona com estas matrizes:

Locando do lado esquerdo da equação na propriedade associativa, vemos que (XY)Z(XY)Z(XY)Z dá:

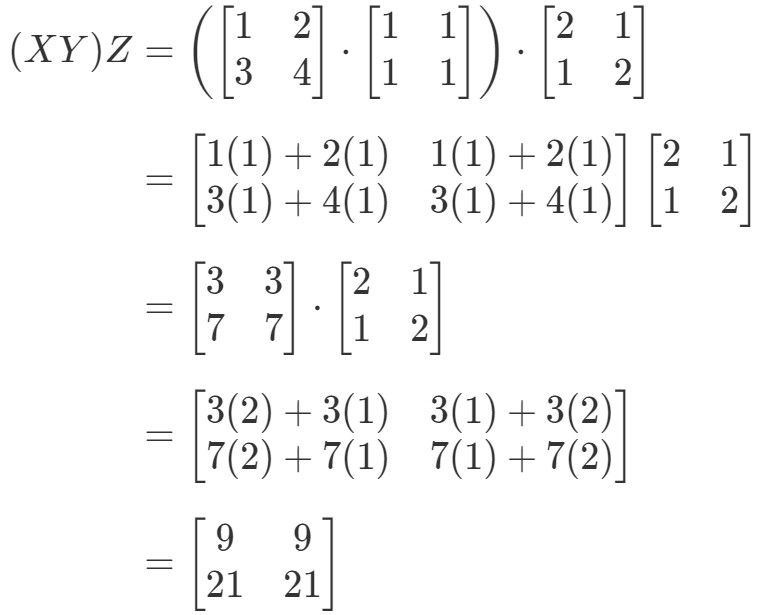
Agora olhando para o lado direito da equação na propriedade associativa, vemos que X(YZ)X(YZ)X(YZ) dá:

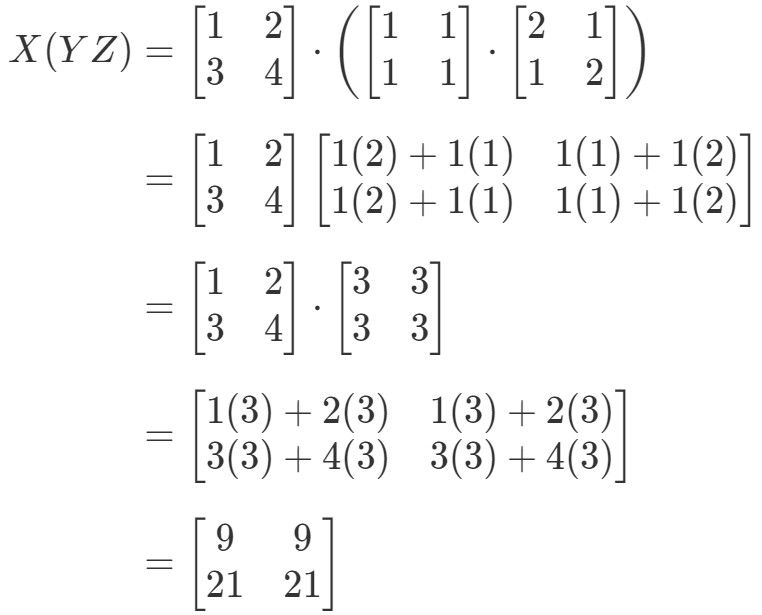
Veja como o lado esquerdo e o lado direito da equação são ambos iguais. Portanto, sabemos que a propriedade associativa realmente funciona! Mais uma vez, isto significa que a ordem de multiplicação matricial não importa!

Agora a próxima propriedade é a propriedade distributiva. A propriedade distributiva afirma que:

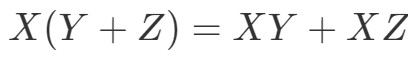
Vemos que também podemos usar a técnica da folha de alumínio para matrizes. Apenas para mostrar que esta propriedade funciona, vamos fazer um exemplo.

Question 7: Mostre que a propriedade distributiva funciona para as seguintes matrizes:

Veja que o lado esquerdo da equação é X(Y+Z)X(Y + Z)X(Y+Z). Daí o cálculo que nos dá:

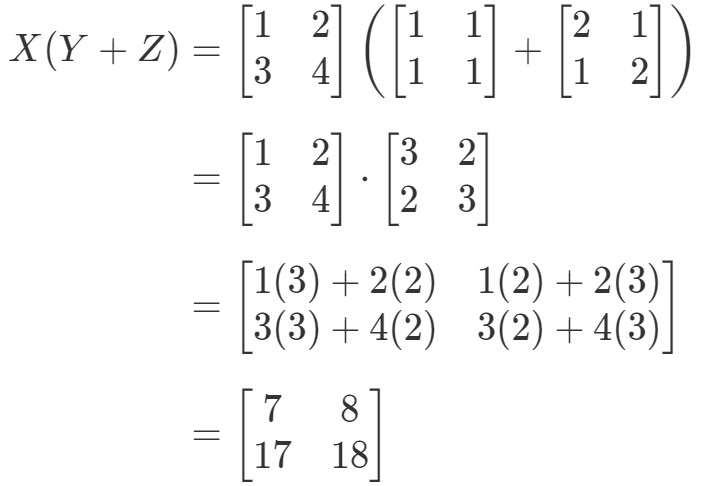
Agora vamos verificar se o lado direito da equação nos dá exatamente a mesma coisa. Note que o lado direito da equação é XY+XZXY + XZXY+XZZ. Computando isto nos dá:

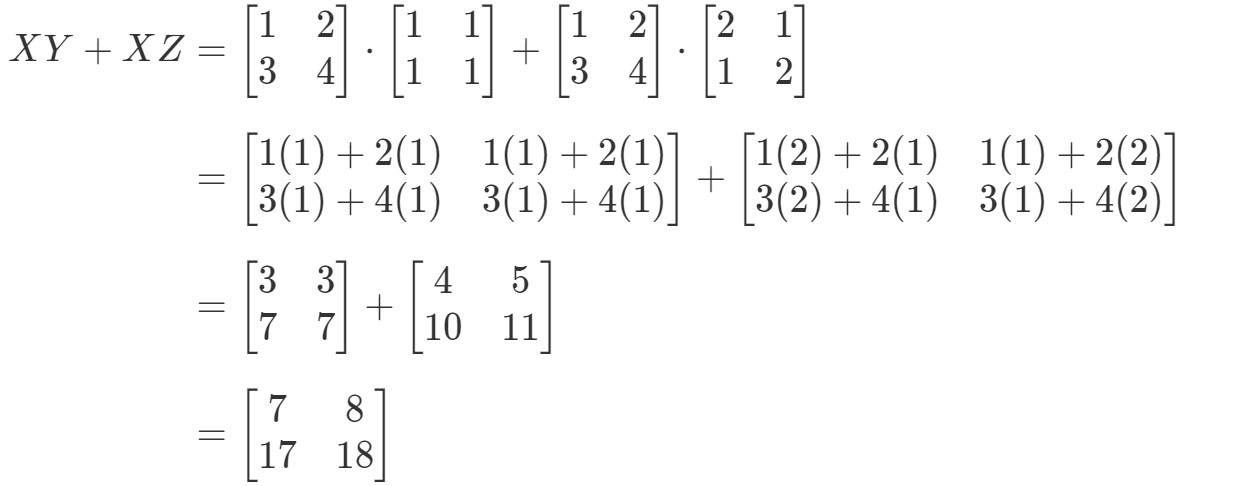
Note que o lado esquerdo da equação é exatamente o mesmo que o lado direito da equação. Portanto, podemos confirmar que a propriedade distributiva realmente funciona.

Is Matrix Multiplication Commutative?

Sabemos que a multiplicação matricial satisfaz tanto as propriedades associativas quanto as distributivas, porém não falamos sobre a propriedade comutativa de forma alguma. Isso significa que a multiplicação matricial não a satisfaz? Na verdade não, e podemos verificar isso com um exemplo.

Questão 8: Se a multiplicação matricial é comutativa, então o seguinte deve ser verdadeiro:

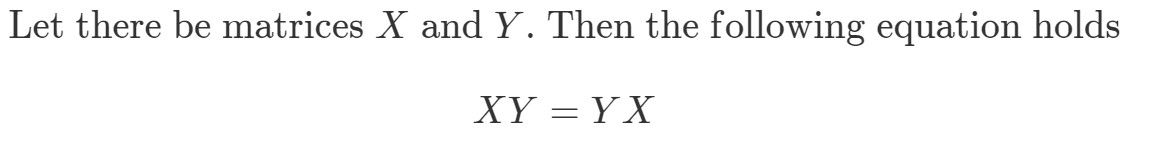
Mostrar que XYeqYXXY eq YXXYeqYX se

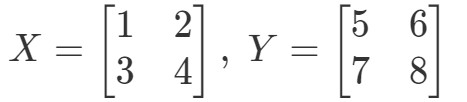
Primeiro calculamos o lado esquerdo da equação. Calculando XYXYXY obtém-se:

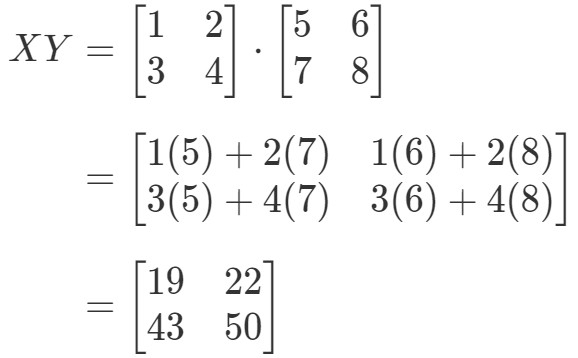
Agora calculando o lado direito da equação, temos:

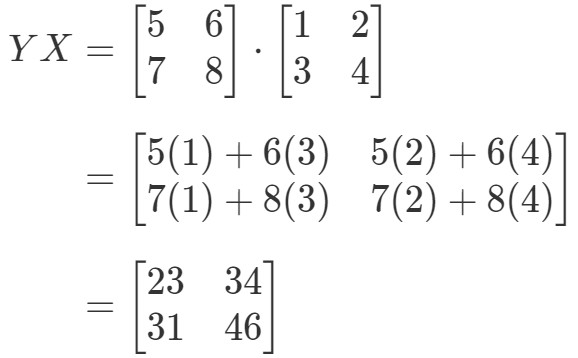
Como pode ver,

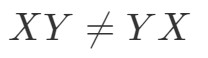
Porque temos

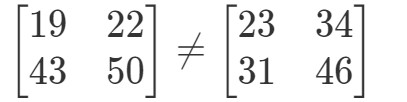
Estas duas matrizes são completamente diferentes.

Agora ainda existem mais algumas propriedades da multiplicação das matrizes. Entretanto, estas propriedades lidam com as matrizes zero e de identidade.

Matrix Multiplication for the Zero Matrix

A propriedade de multiplicação matricial para a matriz zero diz o seguinte:

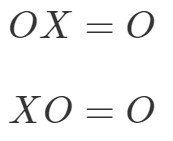
where OOO é uma matriz zero.

Isto significa que se você multiplicar uma matriz zero com outra matriz não-zero, então você terá uma matriz zero. Vamos testar se isto é verdade com um exemplo.

Question 9: Show that the equation OX=OOX = OOX=O e XO=OXO=OXO = OXO=O mantém se:

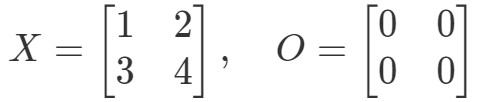
Primeiro olhar para a equação

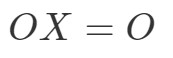
Nota que o cálculo de OXOXOX nos dá:

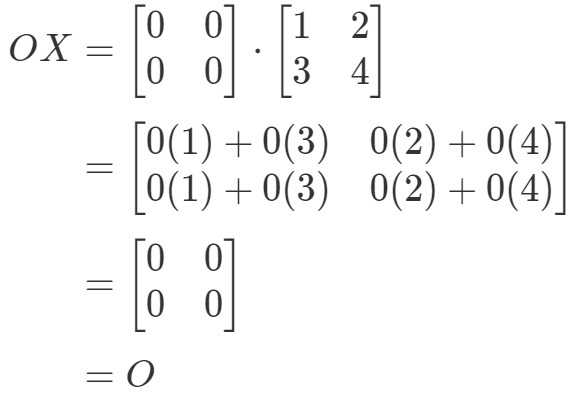
Vemos que OX=OOOX = OOX=O, então a equação se mantém. Da mesma forma, se calcularmos XOXOXO, obtemos:

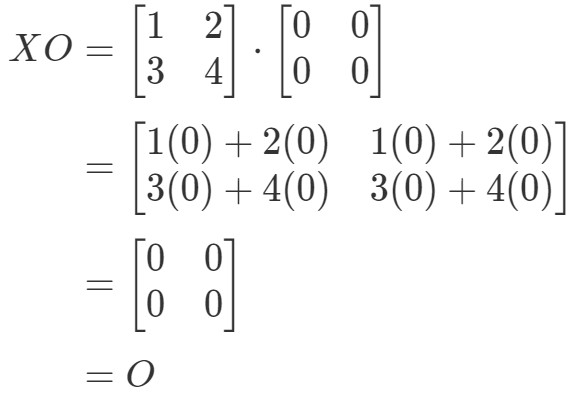
Vemos que a equação XO=OXO = OXO=O se mantém, então estamos feitos.

Matrix Multiplication for the Identity Matrix

Agora e a propriedade de multiplicação de matrizes para matrizes de identidade? Bem, a propriedade diz o seguinte:

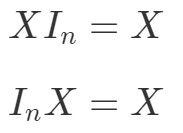
where InI_{n}In é uma matriz de identidade n×nn \times nn×n. Mais uma vez, podemos ver que as seguintes equações se mantêm com um exemplo.

Question 10: Show that the equations XI2=XX I_{2} = XXI2=X and I2X=XI_{2} X = XI2X=X contém as seguintes matrizes

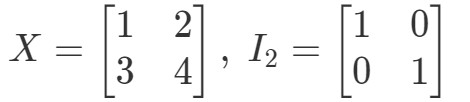
Então para a equação XI2=XX I_{2} = XXI2=X, temos:

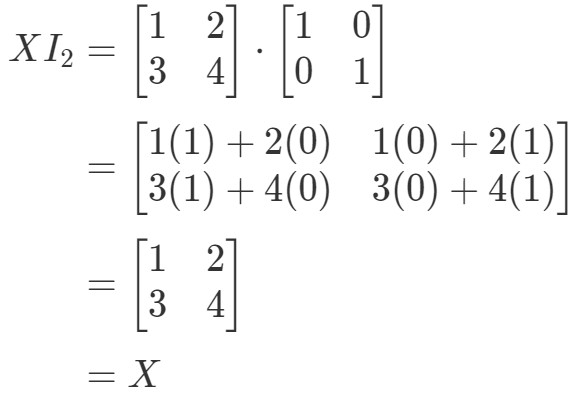
Então a equação se mantém. Similar à equação I2X=XI_{2}X = XI2X=X, nós temos:

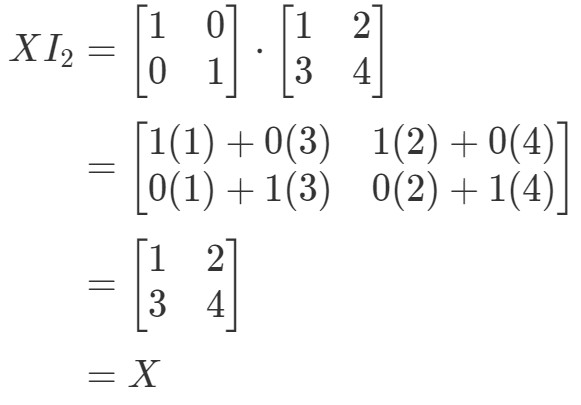
Novamente, a equação se mantém. Assim terminamos com a pergunta, e ambas as equações se mantêm. Isto conclui todas as propriedades da multiplicação matricial. Agora se você quer olhar para uma aplicação real de multiplicação matricial, então eu recomendo que você olhe para este artigo.

https://www.mathsisfun.com/algebra/matrix-multiplying.html