Free Press

Matrixmultiplikation

Es gibt genau zwei Möglichkeiten, Matrizen zu multiplizieren. Die erste Möglichkeit ist die Multiplikation einer Matrix mit einem Skalar. Dies wird als Skalarmultiplikation bezeichnet. Die zweite Möglichkeit ist die Multiplikation einer Matrix mit einer anderen Matrix. Das wird als Matrixmultiplikation bezeichnet.

Skalarmultiplikation

Die Skalarmultiplikation ist eigentlich eine sehr einfache Matrixoperation. Um einen Skalar mit einer Matrix zu multiplizieren, nehmen wir einfach den Skalar und multiplizieren ihn mit jedem Eintrag in der Matrix. Lassen Sie uns ein Beispiel machen.

Frage 1: Berechnen Sie 2A2A2A, wenn

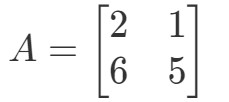
Die Frage fordert uns auf, herauszufinden, was 2A2A2A ist. Mit anderen Worten, wir finden

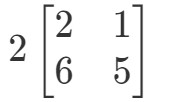
Beachte, dass wir, wenn wir mit 2 zu jedem Eintrag in der Matrix multiplizieren, folgendes erhalten:

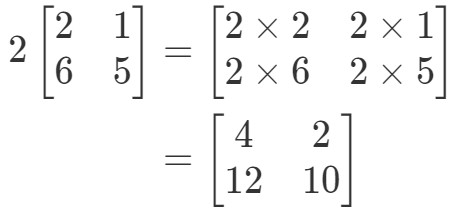
Sehr einfach! Machen wir noch eine.

Frage 2: Berechne 0A0A0A wenn

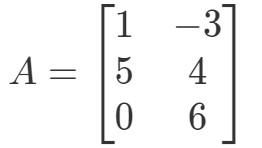
Wieder versuchen wir, 0A0A0A zu finden. Das bedeutet, dass wir nach der Antwort auf

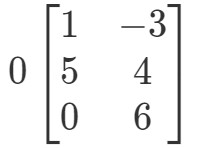
Die Matrix wird seltsam geformt sein, aber das Konzept bleibt das gleiche. Wir werden immer noch den Skalar 0 mit jedem Eintrag in der Matrix multiplizieren. Auf diese Weise erhalten wir:

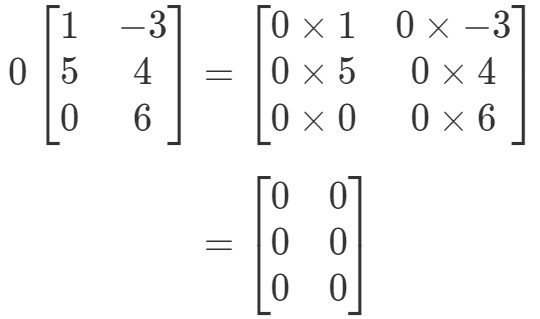
Beachte, dass alle Einträge in der Matrix 0 sind. Dies wird als Nullmatrix bezeichnet, die 3 x 2 ist.

Da wir nun mit der skalaren Multiplikation sehr vertraut sind, warum gehen wir nicht zur Matrixmultiplikation über?

Multiplizieren von Matrizen

Um eine Matrix mit einer anderen Matrix zu multiplizieren, müssen wir zuerst lernen, was das Punktprodukt ist.

Was ist das Punktprodukt?

Das Punktprodukt (auch bekannt als Vektormultiplikation) ist eine Möglichkeit, das Produkt zweier Vektoren zu berechnen. Zum Beispiel seien die beiden Vektoren:

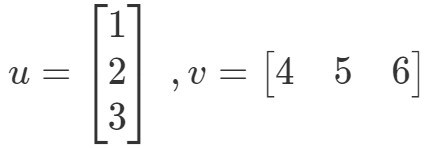
Wie würde ich diese beiden Vektoren multiplizieren? Multiplizieren Sie einfach die entsprechenden Einträge und addieren Sie die Produkte zusammen. Mit anderen Worten:

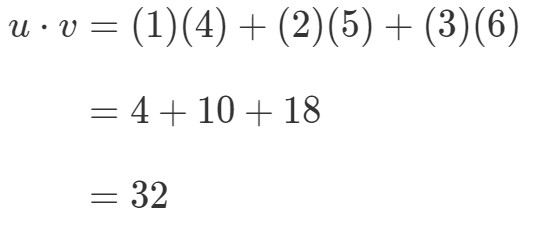
So erhalten wir einen einzigen Wert aus der Multiplikation von Vektoren. Was passiert, wenn einer der beiden Vektoren eine andere Anzahl von Einträgen hat als der andere? Zum Beispiel:

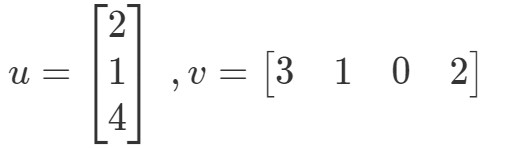
Wenn ich die entsprechenden Einträge multipliziere und zusammenzähle, dann erhalte ich:

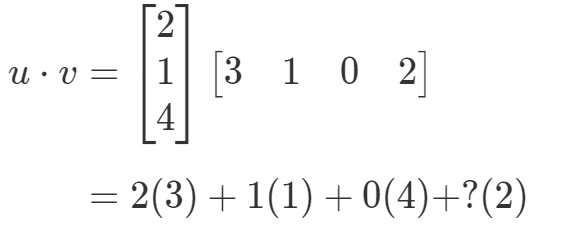
Hier gibt es ein Problem. Die ersten drei Einträge haben entsprechende Einträge, mit denen man multiplizieren kann, aber der letzte Eintrag hat keine. Was machen wir also? Die Antwort ist, dass wir hier nichts tun können. Das bedeutet nur, dass wir das Punktprodukt dieser beiden Vektoren nicht berechnen können.

Als Fazit können wir also nicht das Punktprodukt von zwei Vektoren finden, die eine unterschiedliche Anzahl von Einträgen haben. Sie müssen die gleiche Anzahl von Einträgen haben.

2 x 2 Matrixmultiplikation

Was war also der Sinn, das Punktprodukt zu lernen? Nun, wir werden das Punktprodukt verwenden, wenn wir zwei Matrizen miteinander multiplizieren. Wenn wir eine Matrix mit einer anderen Matrix multiplizieren, müssen wir die Zeilen und Spalten wie einen Vektor behandeln. Genauer gesagt, wir wollen jede Zeile der ersten Matrix als Vektor und jede Spalte der zweiten Matrix als Vektor behandeln. Machen wir ein Beispiel:

Frage 3: Finde A∙BA \bullet BA∙B wenn

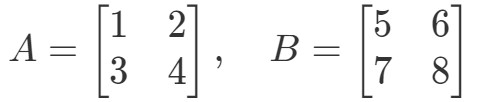
Multipliziert man die beiden Matrizen, so erhält man:

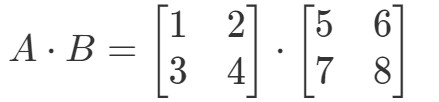
Nun sind die Zeilen und die Spalten, auf die wir uns konzentrieren

wobei r1r_{1}r1 die erste Zeile ist, r2r_{2}r2 die zweite Zeile und c1,c2c_{1}, c_{2}c1,c2 die erste und zweite Spalte. Jetzt werden wir jede Zeile und Spalte, die wir hier sehen, als einen Vektor behandeln.

Beachte hier, dass die Multiplikation einer 2 x 2 Matrix mit einer anderen 2 x 2 Matrix eine 2 x 2 Matrix ergibt. Mit anderen Worten, die Matrix, die wir erhalten, sollte 4 Einträge haben.

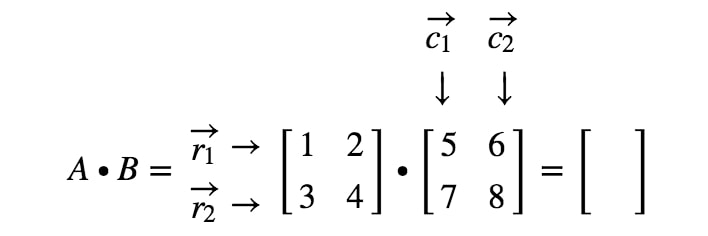
Wie erhalten wir genau den ersten Eintrag? Nun, der erste Eintrag befindet sich in der ersten Zeile und der ersten Spalte. Wir nehmen also einfach das Punktprodukt von r1r_{1}r1 und c1c_{1}c1. Der erste Eintrag ist also

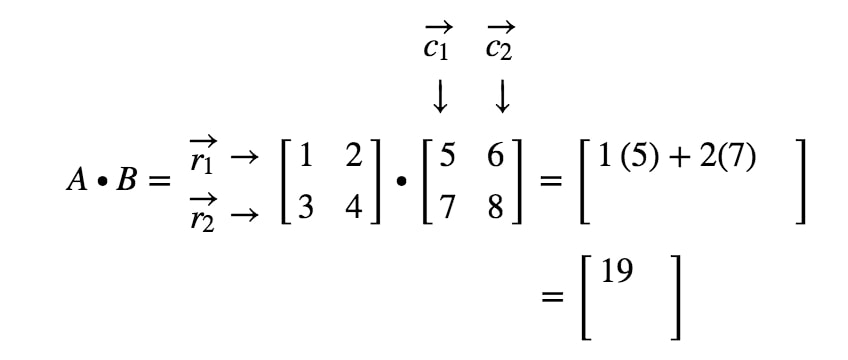
Wie erhalten wir diesmal den zweiten Eintrag? Beachten Sie, dass der zweite Eintrag in der ersten Zeile und der zweiten Spalte steht. Wir nehmen also einfach das Punktprodukt von r1r_{1}r1 und c2c_{2}c2. Der zweite Eintrag lautet also

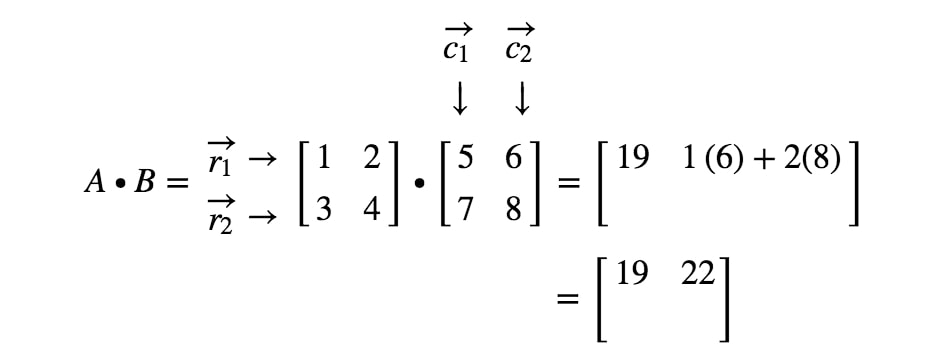
Nun verwenden wir die gleiche Strategie, um die letzten beiden Einträge zu finden. Beachten Sie, dass sich der vorletzte Eintrag in der 2^{nd}2. Zeile und der 1^{st}1. Spalte befindet und der letzte Eintrag in der 2^{nd}2. Zeile und der 2^{nd}2. Wir nehmen also das Punktprodukt von r2r_{2}r2 und c1c_{1}c1, und das Punktprodukt von r2r_{2}r2 und c2c_{2}c2. Das ergibt:

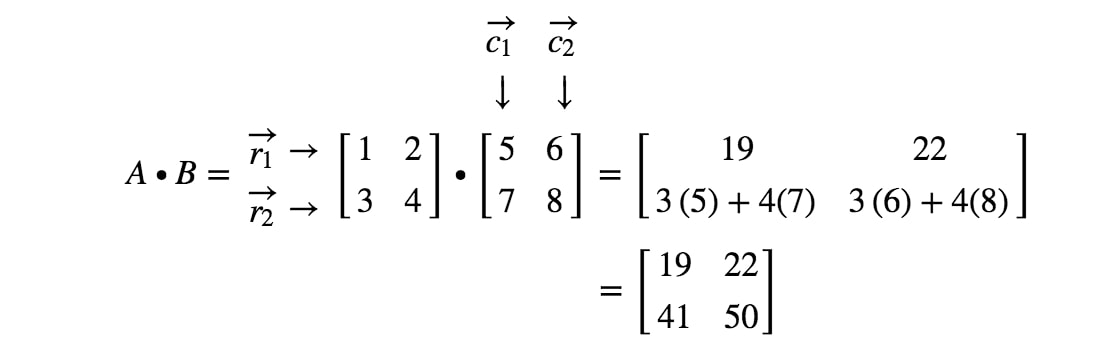
Jetzt sind wir fertig! Das ist das Ergebnis, wenn wir 2 x 2 Matrizen multiplizieren. Im Allgemeinen lautet die Formel für die Matrixmultiplikation von 2 x 2 Matrizen

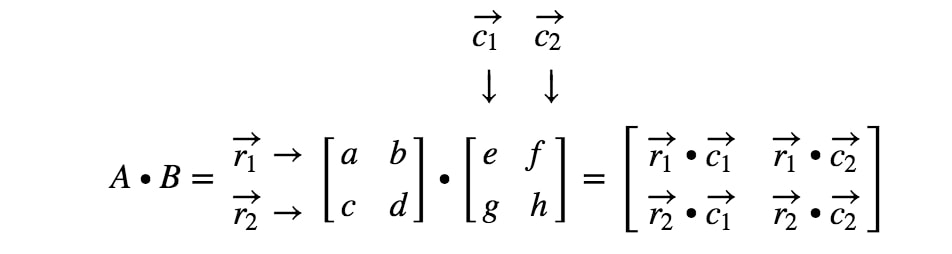
3×3 Matrixmultiplikation

Nun ist der Prozess einer 3 x 3 Matrixmultiplikation dem Prozess einer 2 x 2 Matrixmultiplikation sehr ähnlich. Noch einmal, warum machen wir nicht ein Beispiel für eine Matrixmultiplikation?

Frage 4:Finde A∙BA \bullet BA∙B if

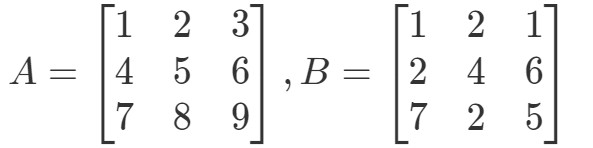
Erst bemerken wir, dass die Multiplikation eine andere 3 x 3 Matrix ergeben sollte. Mit anderen Worten,

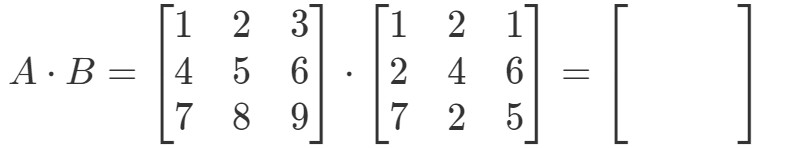
Beschriften wir nun alle unsere Zeilen in der ersten Matrix und die Spalten in der zweiten Matrix.

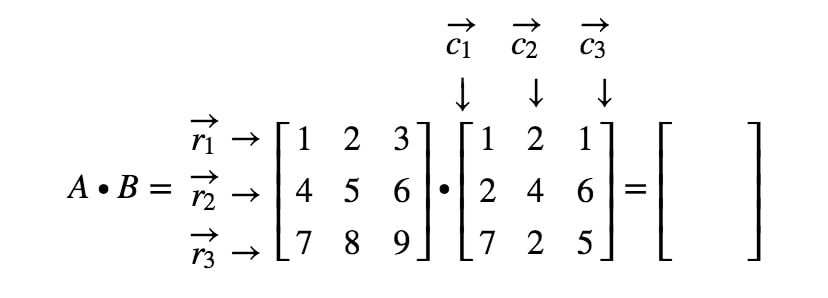
Beachten Sie, dass der erste Eintrag der Matrix in der 1^{st}1sten Zeile und 1^{st}1sten Spalte steht, also nehmen wir das Punktprodukt von r1r_{1}r1 und c1c_{1}c1. Dies ergibt:

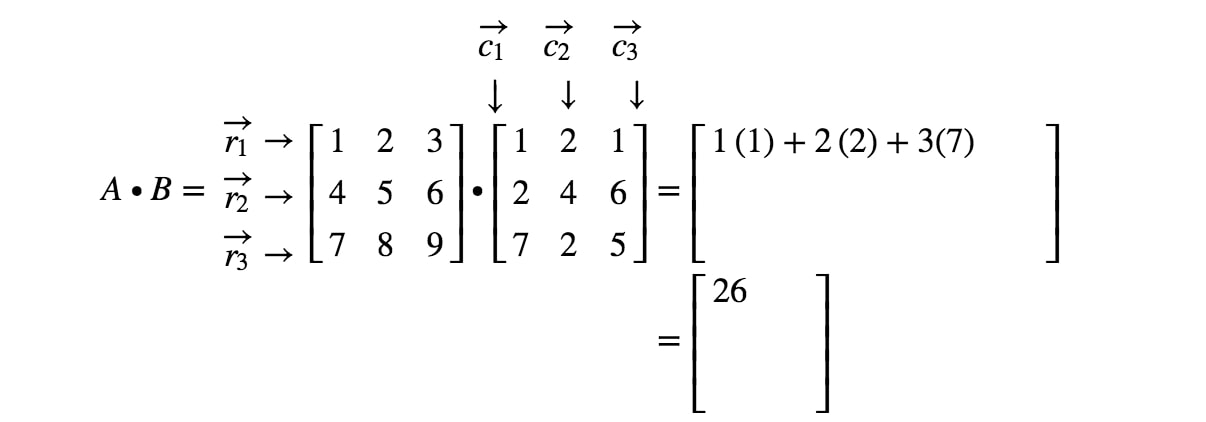
Nun beachten wir, dass der zweite Eintrag der Matrix in der 1st1^{st}1st Zeile und 2nd2^{nd}2nd Spalte liegt. Wir nehmen also das Punktprodukt von r1r_{1}r1 und c2c_{2}c2. Dies ergibt:

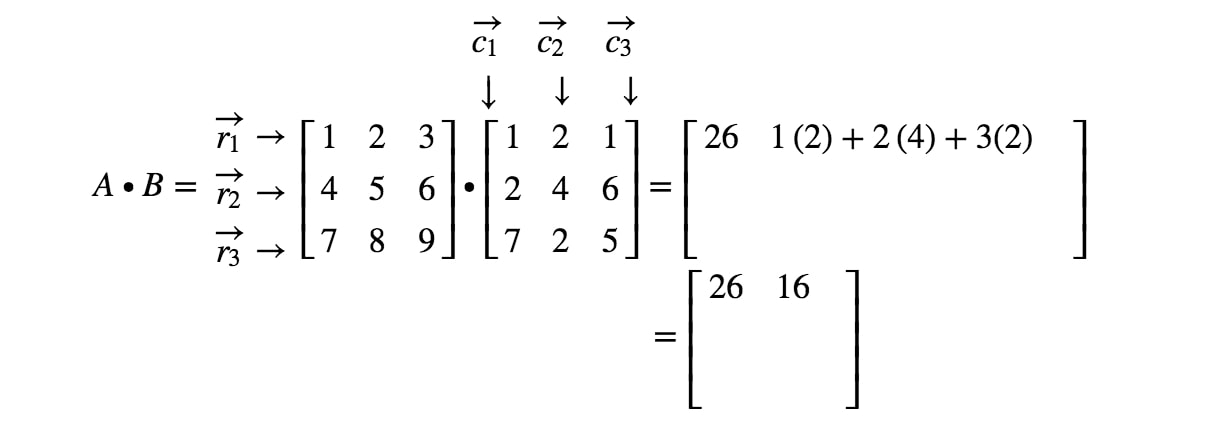
Wenn wir weiterhin alle Einträge suchen und das Punktprodukt entsprechend den Zeilen und Spalten durchführen, dann erhalten wir das Endergebnis:

Wir sind fertig! Je größer die Matrizen sind, desto mühsamer wird die Matrixmultiplikation. Das liegt daran, dass wir mit immer mehr Zahlen umgehen müssen! Im Allgemeinen lautet die Formel für die Matrizenmultiplikation für 3 x 3 Matrizen

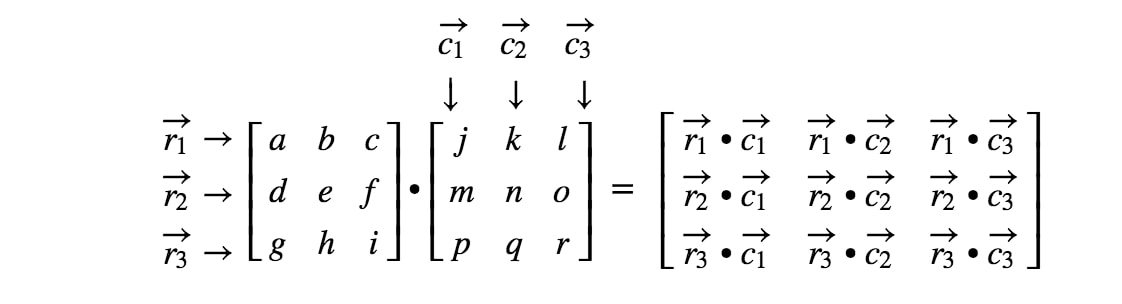
Wie multipliziert man Matrizen mit unterschiedlichen Dimensionen?

Bis jetzt haben wir Matrizen mit den gleichen Dimensionen multipliziert. Außerdem wissen wir, dass die Multiplikation zweier Matrizen mit der gleichen Dimension eine Matrix mit den gleichen Dimensionen ergibt. Aber was passiert, wenn wir eine Matrix mit unterschiedlichen Dimensionen multiplizieren? Wie können wir die Dimensionen der berechneten Matrix ermitteln? Zuerst müssen wir sehen, dass die Multiplikation der Matrizen eine definierte Matrix ergibt.

Ist die Matrix definiert?

Es gibt Fälle, in denen es nicht möglich ist, zwei Matrizen miteinander zu multiplizieren. In diesen Fällen nennen wir die Matrix undefiniert. Woran erkennt man, dass sie undefiniert ist?

Das Produkt zweier Matrizen ist nur dann definiert, wenn die Anzahl der Spalten der ersten Matrix gleich der Anzahl der Zeilen der zweiten Matrix ist.

Lassen Sie uns versuchen, diese Definition in diesem Beispiel anzuwenden.

Frage 5: Lassen Sie

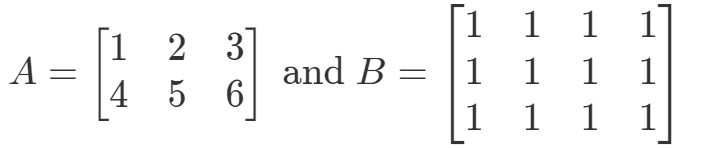
Ist A∙BA \Bullet BA∙B definiert?

Zunächst ist zu beachten, dass die erste Matrix 3 Spalten hat. Auch die zweite Matrix hat 3 Zeilen. Da sie beide gleich 3 sind, weiß ich, dass A∙BA \bullet BA∙B definiert ist.

Nun, da wir wissen, dass es definiert ist, wie können wir die Dimensionen von A∙BA \bullet BA∙B kennen?

Die Dimensionseigenschaft

Um die Dimensionen von A∙BA \bullet BA∙B zu finden, müssen wir zunächst die Dimensionen von und getrennt betrachten.

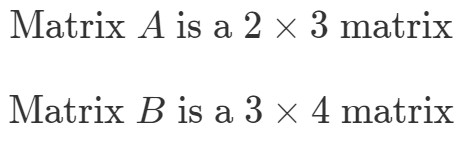
Nun stellen wir die Dimensionen der Matrizen wie folgt nebeneinander:

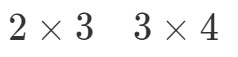
Was wir nun tun werden, ist die erste Zahl und die letzte Zahl zu nehmen und sie zu kombinieren, um die Dimensionen von A∙BA \bullet BA∙B zu erhalten. Die erste Zahl ist 2 und die letzte Zahl ist 4. Die Dimensionen von A∙BA \bullet BA∙B sind also:

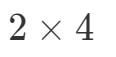
Nun, da wir die Dimensionen der Matrix kennen, können wir einfach jeden Eintrag berechnen, indem wir die Punktprodukte verwenden. So erhalten wir:

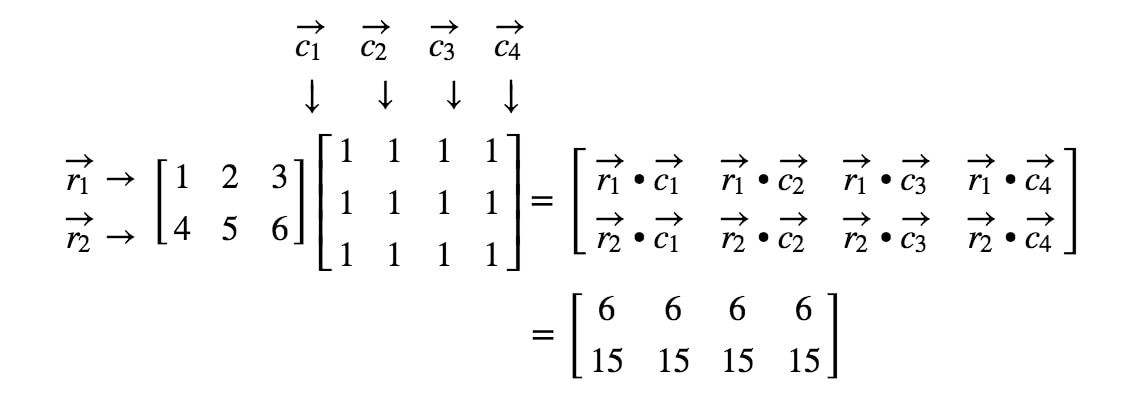
Da wir nun wissen, wie man Matrizen sehr gut multiplizieren kann, sollten wir uns einige Regeln für die Matrixmultiplikation ansehen?

Eigenschaften der Matrixmultiplikation

Welche Eigenschaften hat die Matrixmultiplikation eigentlich? Lassen Sie uns zunächst alles formal definieren.

Lassen Sie X,Y,ZX, Y, ZX,Y,Z Matrizen sein, InI_{n}In sei eine Identitätsmatrix und OnO_{n}On eine Nullmatrix. Wenn alle fünf Matrizen die gleichen Dimensionen haben, gelten folgende Eigenschaften für die Matrix-Multiplikation:

Die assoziative Eigenschaft besagt, dass die Reihenfolge der Multiplikation keine Rolle spielt. Mit anderen Worten, wenn man X∙YX \bullet YX∙Y berechnet und dann mit ZZZ multipliziert, erhält man das gleiche Ergebnis wie wenn man Y∙ZY \bullet ZY∙Z berechnet und dann mit XXX multipliziert. Machen wir ein Beispiel.

Frage 6: Zeigen Sie, dass die assoziative Eigenschaft mit diesen Matrizen funktioniert:

Betrachten wir die linke Seite der Gleichung in der assoziativen Eigenschaft, sehen wir, dass (XY)Z(XY)Z(XY)Z ergibt:

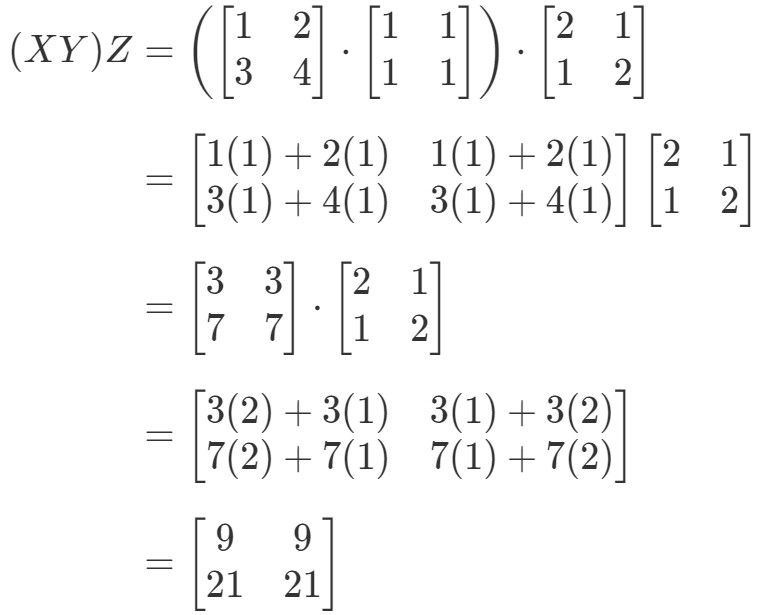
Betrachten wir nun die rechte Seite der Gleichung in der assoziativen Eigenschaft, so sehen wir, dass X(YZ)X(YZ)X(YZ) ergibt:

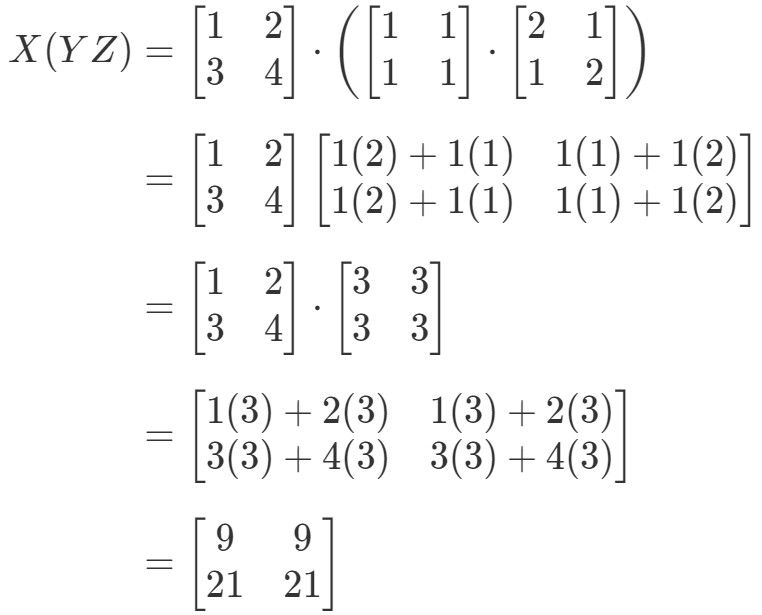
Sie sehen, dass die linke Seite und die rechte Seite der Gleichung beide gleich sind. Wir wissen also, dass die assoziative Eigenschaft tatsächlich funktioniert! Das bedeutet wiederum, dass die Reihenfolge der Matrixmultiplikation keine Rolle spielt!

Die nächste Eigenschaft ist die distributive Eigenschaft. Die distributive Eigenschaft besagt, dass:

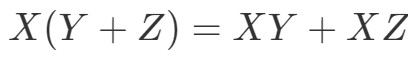
Wir sehen, dass wir die Folientechnik auch für Matrizen verwenden dürfen. Um zu zeigen, dass diese Eigenschaft funktioniert, machen wir ein Beispiel.

Frage 7: Zeigen Sie, dass die Distributiv-Eigenschaft für die folgenden Matrizen funktioniert:

Sehen Sie, dass die linke Seite der Gleichung X(Y+Z)X(Y + Z)X(Y+Z) ist. Die Berechnung ergibt also:

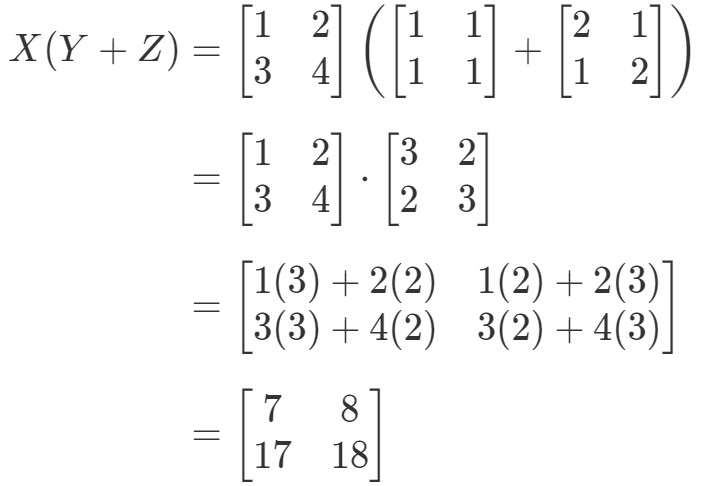
Nun wollen wir prüfen, ob die rechte Seite der Gleichung genau dasselbe ergibt. Beachte, dass die rechte Seite der Gleichung XY+XZXY + XZXY+XZ ist. Die Berechnung ergibt:

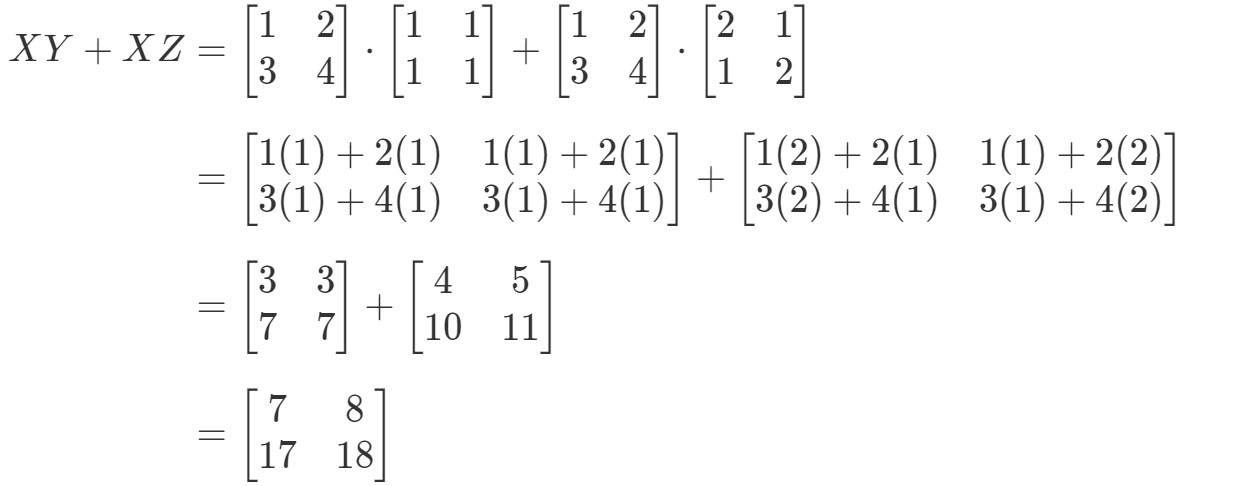
Beachte, dass die linke Seite der Gleichung genau das Gleiche ist wie die rechte Seite der Gleichung. Wir können also bestätigen, dass die distributive Eigenschaft tatsächlich funktioniert.

Ist die Matrixmultiplikation kommutativ?

Wir wissen, dass die Matrixmultiplikation sowohl die assoziative als auch die distributive Eigenschaft erfüllt, aber wir haben überhaupt nicht über die kommutative Eigenschaft gesprochen. Bedeutet das, dass die Matrixmultiplikation diese Eigenschaft nicht erfüllt? Das tut sie tatsächlich nicht, und wir können das anhand eines Beispiels überprüfen.

Frage 8: Wenn die Matrixmultiplikation kommutativ ist, dann muss Folgendes wahr sein:

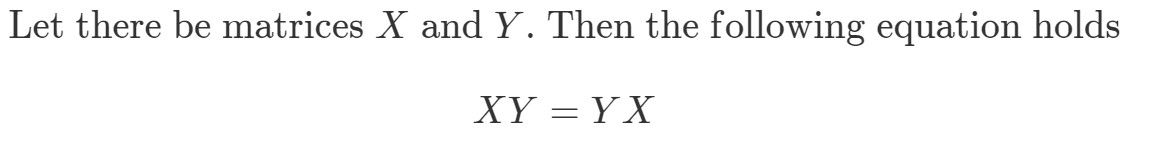
Zeige, dass XYeqYXXY eq YXXYeqYX ist, wenn

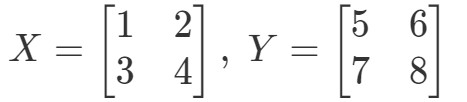
Zuerst berechnen wir die linke Seite der Gleichung. Die Berechnung von XYXYXY ergibt:

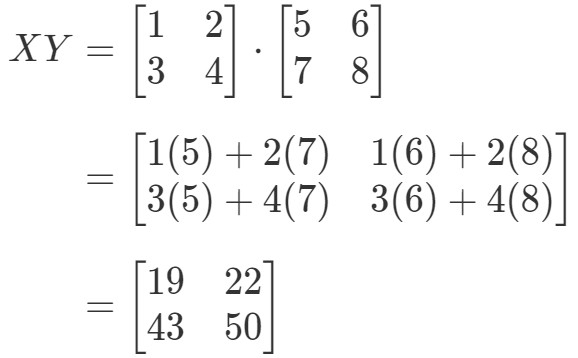
Nun berechnen wir die rechte Seite der Gleichung, wir haben:

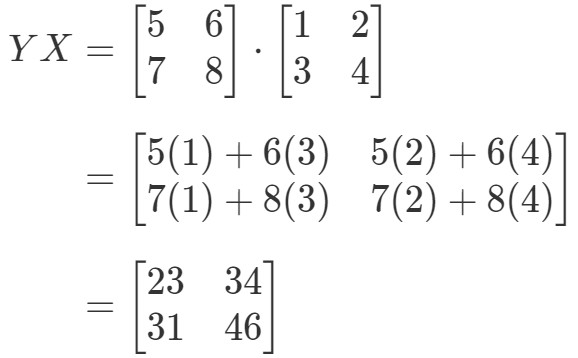
Wie man sieht,

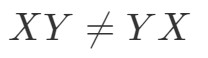
Denn wir haben

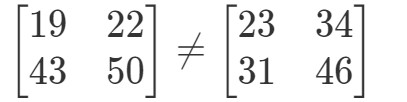
Diese beiden Matrizen sind völlig unterschiedlich.

Nun gibt es noch ein paar weitere Eigenschaften der Multiplikation von Matrizen. Diese Eigenschaften beziehen sich jedoch auf die Null- und Identitätsmatrizen.

Matrixmultiplikation für die Nullmatrix

Die Eigenschaft der Matrixmultiplikation für die Nullmatrix besagt folgendes:

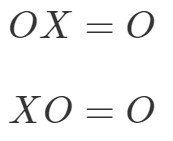
wobei OOO eine Nullmatrix ist.

Das heißt, wenn man eine Nullmatrix mit einer anderen Nicht-Nullmatrix multipliziert, dann erhält man eine Nullmatrix. Testen wir anhand eines Beispiels, ob das stimmt.

Frage 9: Zeigen Sie, dass die Gleichung OX=OOX = OOX=O und XO=OXO = OXO=O gilt, wenn:

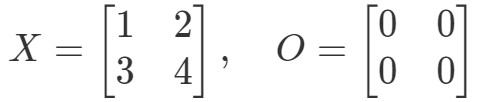
Betrachten wir zunächst die Gleichung

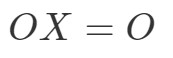
Beachten Sie, dass die Berechnung von OXOXOX ergibt:

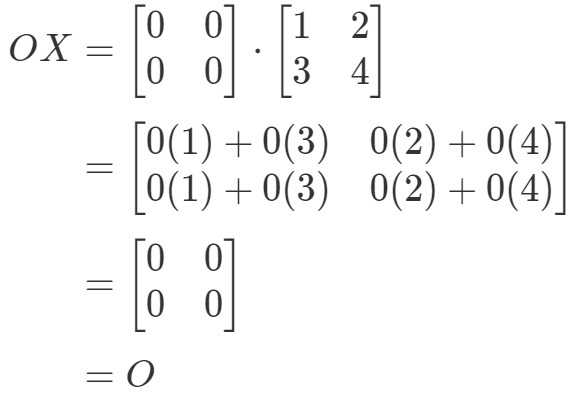
Wir sehen, dass OX=OOX = OOX=O ist, also gilt die Gleichung. Wenn wir XOXOXO berechnen, erhalten wir:

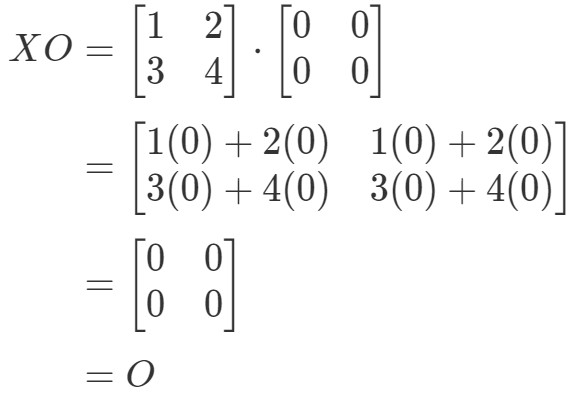
Wir sehen, dass die Gleichung XO=OXO = OXO=O gilt, also sind wir fertig.

Matrixmultiplikation für die Identitätsmatrix

Was ist nun mit der Eigenschaft der Matrixmultiplikation für Identitätsmatrizen? Nun, die Eigenschaft besagt folgendes:

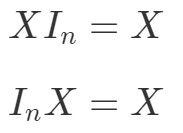
wobei InI_{n}In eine n×nn \times nn×n Identitätsmatrix ist. Auch hier können wir anhand eines Beispiels sehen, dass die folgenden Gleichungen gelten.

Frage 10: Zeigen Sie, dass die Gleichungen XI2=XX I_{2} = XXI2=X und I2X=XI_{2} X = XI2X=X mit den folgenden Matrizen gilt

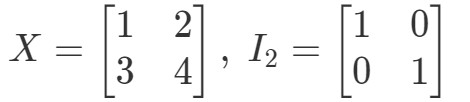
Für die Gleichung XI2=XX I_{2} = XXI2=X gilt also:

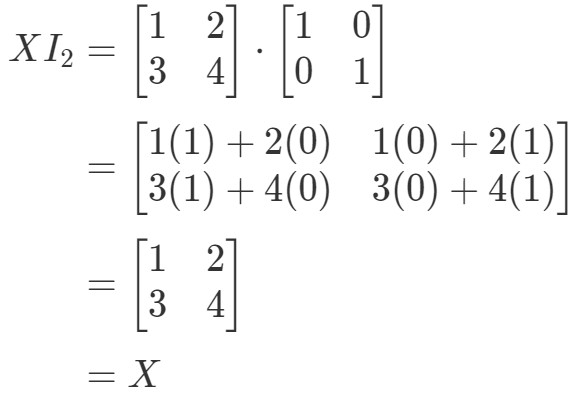
Die Gleichung ist also gültig. Ähnlich wie bei der Gleichung I2X=XI_{2}X = XI2X=X, haben wir:

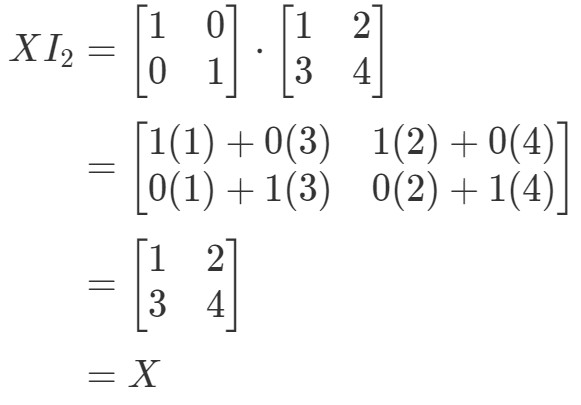
Auch hier gilt die Gleichung. Damit sind wir mit der Frage fertig, und beide Gleichungen sind gültig, womit alle Eigenschaften der Matrixmultiplikation abgeschlossen sind. Wenn Sie nun eine Anwendung der Matrixmultiplikation im wirklichen Leben sehen wollen, empfehle ich Ihnen diesen Artikel.

https://www.mathsisfun.com/algebra/matrix-multiplying.html