
Fern
Hier ist eine aktuelle Frage von Leser Pehr aus Schweden:
Hallo,
Zunächst einmal, wunderbare Seite. Ich liebe sie.
Ich habe den Abschnitt über Polarkoordinaten studiert, in der Hoffnung, mein Wissen über die gleichwinklige Spirale zu erweitern. Die interaktiven Werkzeuge sind großartig, obwohl es mir schwer fällt, die genaue mathematische Lösung abzuleiten, warum die resultierende Funktion für die goldene Spirale
r = ae^(b(theta)) ist
Für einige Hintergrundinformationen zu Pehrs Frage siehe:
Polarkoordinaten, Kurven in Polarkoordinaten und gleichwinklige Spirale
Spiralen sind in der Natur weit verbreitet und haben Mathematiker seit Jahrhunderten inspiriert.

Aloe-Spirale

Spiralgalaxie NGC 5194
Logarithmische Spiralen
Die Goldene Spirale, nach der Pehr fragt, ist ein Spezialfall der logarithmischen Spirale.
Logarithmische Spiralen wachsen so, dass der Winkel einer Linie vom Mittelpunkt der Spirale zur Tangente an die Kurve in diesem Punkt konstant ist. Deshalb werden sie auch als „gleichwinklige“ Spiralen bezeichnet.
Um zu sehen, was das bedeutet, sind die 3 spitzen Winkel, die im folgenden Farnbild markiert sind, ungefähr 80°

Gleichwinkliger Farn
Wir verwenden normalerweise Funktionen in Polarkoordinaten, wenn wir Spiralen beschreiben. Wenn wir sonst gewöhnliche rechtwinklige Koordinaten verwenden, werden die Formeln sehr komplex.
Die Formel für eine logarithmische Spirale in Polarkoordinaten lautet:
r = aeθ cot b
wobei
r der Abstand vom Ursprung (oder „Pol“) ist
a eine Konstante ist
θ der Winkel (im Bogenmaß) zur horizontalen Achse. Die Koordinaten eines Punktes auf der Kurve in Polarkoordinaten sind also gegeben durch (r, θ).
b ist der Winkel (im Bogenmaß – der „gleiche“ Winkel), den die Linie vom Mittelpunkt der Spirale mit der Tangente an die Spirale bildet. Im obigen Farnfall ist b ≈ 1,4 Bogenmaß (≈ 80°).
Als Folge der Art und Weise, wie wir die logarithmische Spirale definiert haben, ist das Verhältnis der Abstände vom Zentrum zu jedem Spiralarm eines benachbarten Paares konstant.

Spiralarme in konstantem Verhältnis
Das Verhältnis
Abstand zum ersten Arm: Abstand zum zweiten Arm
= 29:69
≈ 0.42
Das andere Verhältnis
Abstand zum zweiten Arm: Abstand zum dritten Arm
= 69:154
≈ 0.45
Wir sehen, dass die Verhältnisse fast gleich sind. (In einer tatsächlichen logarithmischen Spirale sind sie genau gleich. Die Wahl des Startpunktes für den Farn ist keine exakte Wissenschaft).
Goldene Spirale
Die Goldene Spirale ist ein Spezialfall der logarithmischen Spirale.
Wir können die allgemeine logarithmische Spirale als Funktion in Polarkoordinaten schreiben, indem wir t wie folgt verwenden:
r(t) = aet cot b
Anmerkung: Normalerweise verwenden wir θ für die unabhängige Variable, aber wir verwenden oft t, da wir uns vorstellen können, dass die Spirale über die Zeit verfolgt wird. Außerdem ist es einfacher zu tippen!
Die Goldene Spirale hat die besondere Eigenschaft, dass für jede 1/4-Drehung (90° oder π/2 im Bogenmaß) der Abstand vom Mittelpunkt der Spirale um den Goldenen Schnitt φ = 1,6180 zunimmt.
Damit dies geschieht, muss cot b den Wert annehmen (der sich aus der Lösung unserer Funktion ergibt):
![]()
Mit diesem Wert und für den einfachen Fall, dass a = 1 ist, wird unsere Funktion:
r(t) = e0.30635t
Wir werden von nun an das ausgezeichnete kostenlose Graphentool GeoGebra verwenden.
Aufstellen der Goldenen Spirale mit GeoGebra
Wenn wir nun unsere Funktion auf gewöhnlichen rechtwinkligen Koordinatenachsen in GeoGebra grafisch darstellen, erhalten wir die folgende Exponentialkurve. Man beachte, dass r mit zunehmendem t immer weiter ansteigt (steiler wird).
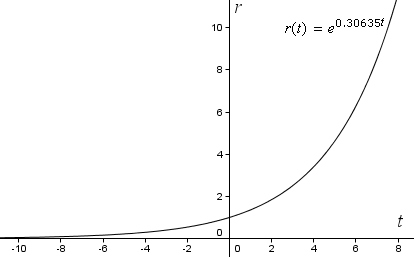
Um aber eine Spirale zu sehen, müssen wir die Kurve in Polarkoordinaten darstellen.
Um die Polarform (die wir haben) in Geogebra in die Rechteckform umzuwandeln (die wir für den Graphen brauchen), müssen wir die folgende Funktion aufstellen und grafisch darstellen:
a(t) = (r(t) cos(t), r(t) sin(t))
Lassen Sie uns ein paar wichtige Werte ersetzen, um zu sehen, was dieser Ausdruck bedeutet. Ausgehend von t = 0 erhalten wir den Anfangspunkt der Kurve:
a(0) = (r(0) cos(0), r(0) sin(0))
= (1×1, 1×0)
= (1, 0)
Das bedeutet, wir beginnen 1 Einheit vom Ursprung entlang der positiven x-Achse. Der Ausgangspunkt ist in der folgenden Grafik der Spirale zu sehen.
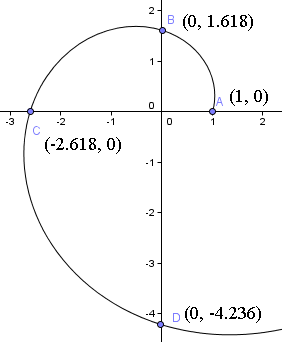
Als nächstes drehen wir eine Vierteldrehung und finden bei t = π/2,
a(π/2) = (r(π/2) cos(π/2), r(π/2) sin(π/2))
= (1,618×0, 1,618×1)
= (0, 1,618)
Beachte, dass wir uns jetzt 1,618 Einheiten vom Ursprung auf der y-Achse befinden. Das heißt, φ ist das 1,6180-fache der Entfernung, von der wir ausgegangen sind.
Eine weitere Drehung um eine Vierteldrehung bringt uns zu t = π, wobei:
a(π) = (r(π) cos(π), r(π) sin(π))
= (-2,618×1, -2,618×0)
= (-2,618, 0)
Wir sind jetzt 2,618 Einheiten vom Ursprung entlang der negativen x-Achse entfernt, oder φ = 1,6180 mal die Entfernung vom Ursprung, die wir bei der letzten Vierteldrehung hatten.
Anmerkung:
φ2 = 2,6180
Wir können unsere nächste Position entlang der negativen y-Achse berechnen, indem wir diesen letzten Wert einfach mit φ = 1,6180 multiplizieren, was uns ergibt:
φ3 = 4,23606…
Die Spirale schneidet also die y-Achse bei (0, -4,236).
Eine weitere Vierteldrehung bringt uns zu φ4 = 6,85410… Einheiten entlang der positiven y-Achse, also (6,854, 0).
Wir können sehen, dass diese Werte in unserem obigen Spiraldiagramm korrekt sind.
Wenn wir weitermachen, erhalten wir eine Spirale wie folgt (das sind 2 vollständige Umdrehungen oder 4π = 720°):
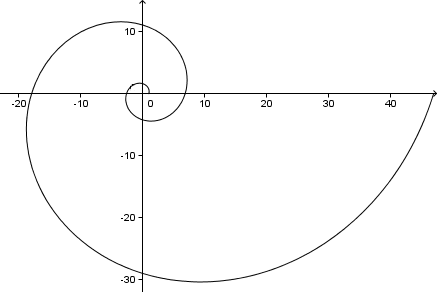
Nebenbei, da in diesem Problem
cot b = 0.30635
dann
b = arccot 0,30635 = 1,274 Radiant oder etwa 73°
Dies ist der Winkel, den unsere Spiralarme mit einer Linie vom Zentrum der Spirale bilden. In der obigen Grafik ist zu sehen, dass jeder Spiralarm einen Winkel von 73° mit der x-Achse (und der y-Achse oder einer beliebigen Linie vom Zentrum aus) bildet.
Annäherung an die Goldene Spirale mit Hilfe von Kreisbögen
Wir können eine Spirale erhalten, die der Goldenen Spirale recht ähnlich sieht, indem wir Kreisbögen verwenden, die durch den Goldenen Schnitt an Größe zunehmen, wie folgt.
Wir beginnen mit einem 1×1-Quadrat und zeichnen einen Bogen, Mittelpunkt C, durch 2 Ecken, so dass die Seiten des Quadrats den Bogen tangieren (d.h. sie berühren sich nur einmal).
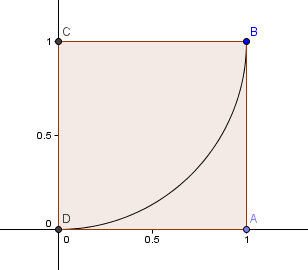
Als nächstes legen wir ein Quadrat mit der Seitenlänge φ = 1.6180 über unser erstes Quadrat und konstruieren einen weiteren Kreisbogen, Zentrum E, wie zuvor:
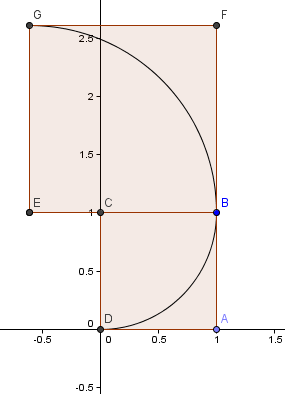
Unser nächstes Quadrat geht nach links und hat die Seitenlänge φ2 = 2.6180 = 1 + φ.
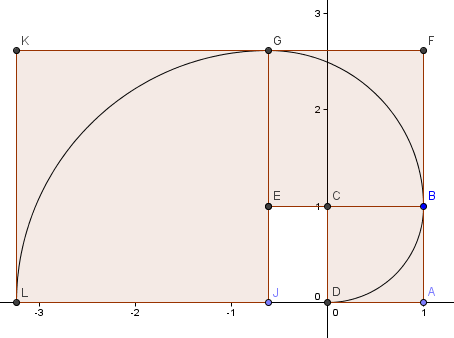
Wir setzen das Muster fort (wir sind eine weitere Runde gegangen) und erhalten eine Spirale, die unserer Goldenen Spirale von vorhin sehr ähnlich sieht.
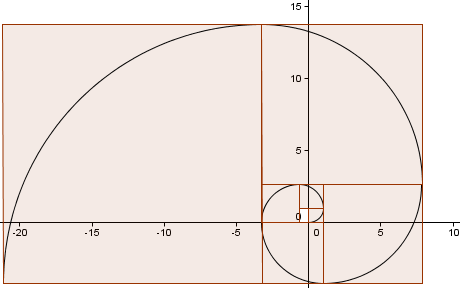
Wie nahe ist unsere Annäherung?
Im Wikipedia-Artikel über die Goldene Spirale gibt es ein Bild, das behauptet, dass die obige Spirale und die Goldene Spirale in ihrer Form sehr ähnlich sind.
Hier ist das Bild:
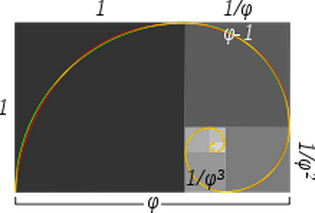
In der Bildunterschrift heißt es:
Näherungsweise und echte goldene Spiralen: Die grüne Spirale besteht aus Viertelkreisen, die das Innere jedes Quadrats tangieren, während die rote Spirale eine goldene Spirale ist, eine besondere Art von logarithmischer Spirale. Sich überschneidende Teile erscheinen gelb. Die Länge der Seite eines größeren Quadrats zum nächstkleineren Quadrat entspricht dem Goldenen Schnitt.
Können wir das nachbilden?
In der Abbildung unten ist die rote Kurve der erste Teil der Goldenen Spirale, die wir oben konstruiert haben, während die grüne Kurve auf der Annäherung an die Vierteldrehung basiert, an der wir gerade gearbeitet haben.
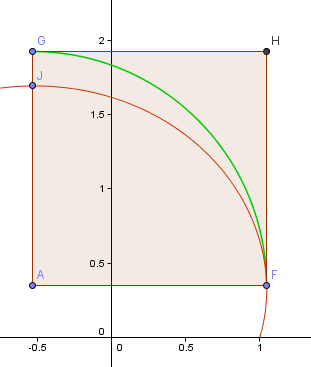
Der Punkt F ist der „rechteste“ Punkt auf der Spirale, der mein Ausgangspunkt für den Vierteldrehungsbogen sein wird. Der Punkt J ist der höchste Punkt dieses Teils der Spirale.
Der Punkt A ist der Schnittpunkt der horizontalen und der vertikalen Linie, die durch F bzw. J verlaufen, und dies wird der Mittelpunkt meines Bogens sein.
Nun liegt der Bogen GF überhaupt nicht in der Nähe des entsprechenden Teils der Spirale FJ.
Lassen Sie uns einen weiteren Schritt machen und sehen, ob der nächste Teil besser ist.
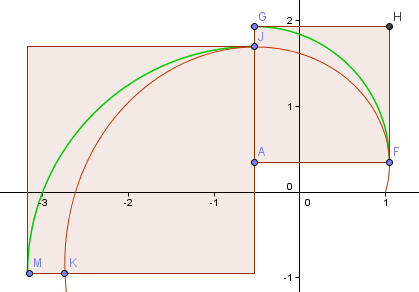
Wie Sie sehen können, ist es schlechter (wie erwartet, da wir uns weiter vom Ursprung entfernt haben und der Spiralarm größer wird).
Es ist klar, dass dies niemals funktionieren wird.
In meiner früheren Goldenen Spirale habe ich jedoch verwendet:
r(t) = e0.30635t
Die Konstante a, hatte den Wert 1.
Wenn wir wollen, dass unsere Näherungsbögen gut zur tatsächlichen Goldenen Spirale passen, müssen wir einen Wert von (wahrscheinlich nicht überraschend)
a = φ = 1,618103399…
Damit erhalten wir die folgenden Kurven, ähnlich der Grafik in Wikipedia.
Die rote Kurve ist die Goldene Spirale,
r(t) = 1,618013 e0,30635t
Die grüne Kurve ist die Sammlung von Kreisbögen.
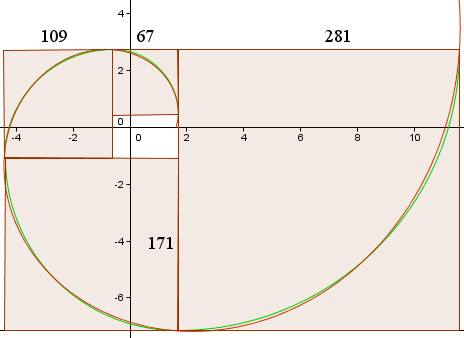
Die Seitenlängen der Quadrate (in Pixeln) sind dargestellt und wir sehen, dass sie ungefähr im Verhältnis 1,618013 stehen…
Goldene Spirale in den Medien
Aus Wolframs Mathworld:
In der Episode „Masterpiece“ (2008) der vierten Staffel des CBS-Krimidramas „Criminal Minds“ werden die Agenten der FBI-Verhaltensanalyseeinheit mit einem Serienmörder konfrontiert, der die Fibonacci-Zahlenfolge verwendet, um die Anzahl der Opfer für jede seiner Tötungsepisoden zu bestimmen. In dieser Folge bemerkt der Charakter Dr. Reid auch, dass die Orte der Morde auf dem Graphen einer goldenen Spirale liegen, und wenn er sich zum Zentrum der Spirale begibt, kann Reid den Standort der Operationsbasis des Mörders bestimmen.
Hier sind weitere interessante Informationen aus Wolfram’s Mathworld:
Logarithmische Spirale
Für die Geeks – Design mit der Goldenen Spirale
Viele glauben, dass Designs, die den Goldenen Schnitt und die Goldene Spirale verwenden, das Auge erfreuen.
Auch Twitter hat kürzlich seine Hauptseite mit der Goldenen Spirale neu gestaltet.
Hier ist ein toller Artikel von einem Mann, der eine goldene Spirale ohne Bilder konstruiert hat. (Vor allem für diejenigen, die sich für Webdesign interessieren)
Goldene Spirale ohne Bilder – mit CSS und jQuery
Wie er in dem Artikel andeutet, ist auch ein Elefantenrüssel nahe an der Goldenen Spirale.

Elefantenrüssel – fast eine Goldene Spirale
Fazit
Die Goldene Spirale ist ein interessantes Thema – eines, das es wert ist, verfolgt zu werden, nicht nur wegen der angenehmen Designs, sondern auch wegen der interessanten Mathematik, die dahinter steckt.
Ich hoffe, das hilft, deine Frage zu beantworten, Pehr!