Free Press

Matriisien kertominen

Matriisien kertomiseen on tasan kaksi tapaa. Ensimmäinen tapa on kertoa matriisi skalaarilla. Tämä tunnetaan skalaarikertolaskuna. Toinen tapa on kertoa matriisi toisella matriisilla. Tämä tunnetaan nimellä matriisikertolasku.

Skalaarikertolasku

Skalaarikertolasku on itse asiassa hyvin yksinkertainen matriisioperaatio. Kun skalaari kerrotaan matriisilla, otetaan yksinkertaisesti skalaari ja kerrotaan se matriisin jokaisella merkinnällä. Tehdään esimerkki.

Kysymys 1: Laske 2A2A2A jos

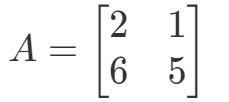
Kysymyksessä pyydetään selvittämään, mikä on 2A2A2A. Toisin sanoen löydämme

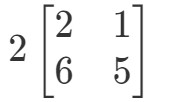
Huomaa, että jos kerromme matriisin jokaiseen merkintään 2, saamme, että:

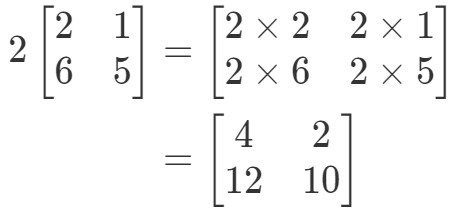
Erittäin yksinkertainen! Tehdään toinenkin.

Kysymys 2: Laske 0A0A0A jos

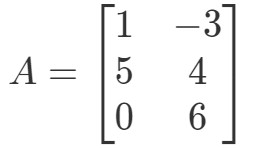
Jälleen kerran yritämme löytää 0A0A0A. Tämä tarkoittaa, että etsimme vastausta

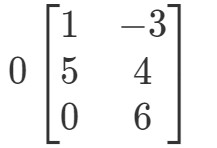
Matriisi on oudon muotoinen, mutta käsite pysyy samana. Monistamme edelleen skalaarin 0 jokaiselle matriisin merkinnälle. Näin tekemällä saamme:

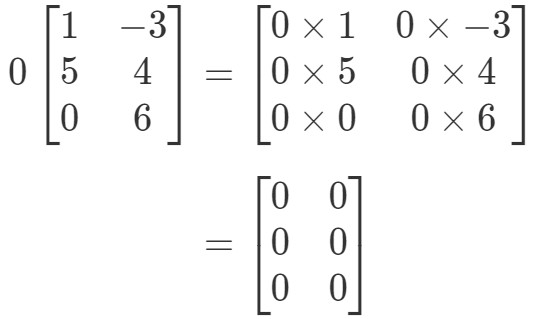
Huomaa, että kaikki matriisin merkinnät ovat 0. Tätä kutsutaan nollamatriisiksi, joka on 3 x 2.

Nyt kun skalaarikertolasku on meille hyvin tuttu, miksi emme siirry matriisikertolaskuun?

Miten kerrotaan matriisit

Jotta voimme kertoa matriisin toisella matriisilla, meidän on ensin opittava, mikä on pistetuotto.

Mikä on pistetuotto?

Pistetuotto (tunnetaan myös nimellä vektorikertolasku) on tapa laskea kahden vektorin tulo. Olkoon esimerkiksi kaksi vektoria:

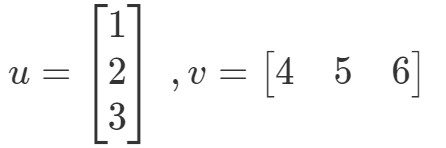
Miten kertoisin nämä kaksi vektoria? Yksinkertaisesti vain kertomalla vastaavat merkinnät ja laskemalla tuotteet yhteen. Toisin sanoen,

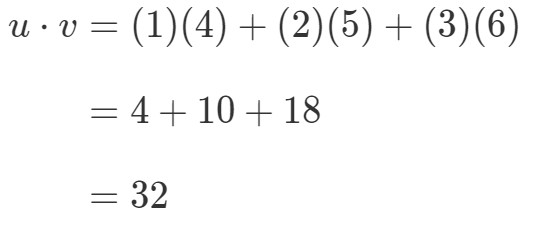
Vektoreiden kertomalla saadaan siis yksi arvo. Huomaa kuitenkin, että molemmilla vektoreilla on sama määrä merkintöjä. entä jos toisella vektorilla on eri määrä merkintöjä kuin toisella? Olkoon esimerkiksi

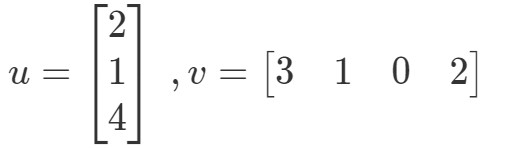
Jos kertoisin vastaavat merkinnät ja laskisin ne kaikki yhteen, niin saisin:

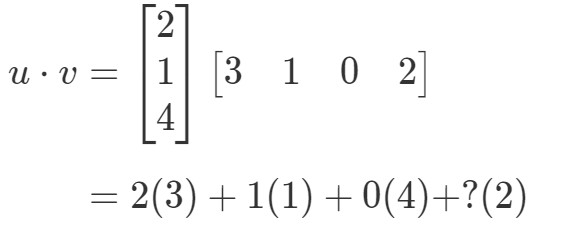
Tässä on ongelma. Kolmella ensimmäisellä merkinnällä on vastaavat merkinnät, joilla kerrotaan, mutta viimeisellä merkinnällä ei ole. Mitä me siis teemme tässä tapauksessa? Vastaus on, ettemme voi tehdä mitään. Tämä tarkoittaa vain sitä, ettemme voi laskea näiden kahden vektorin pistepotentiaalia.

Johtopäätöksenä voimme siis todeta, ettemme voi löytää pistepotentiaalia kahdesta vektorista, joilla on eri määrä merkintöjä. Niillä täytyy olla sama määrä merkintöjä.

2 x 2 matriisikertolasku

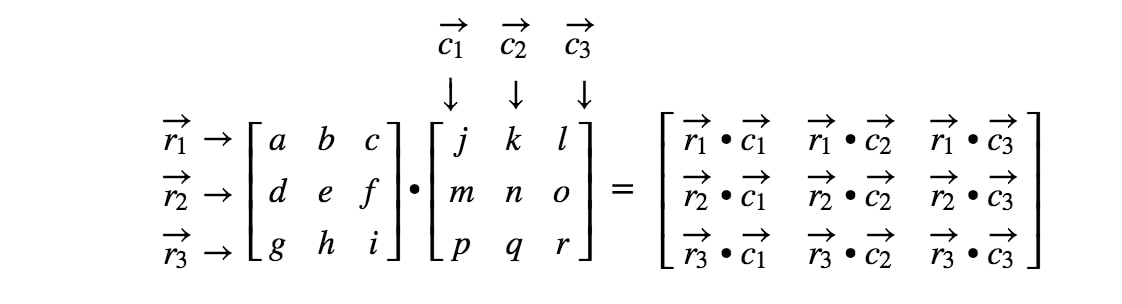
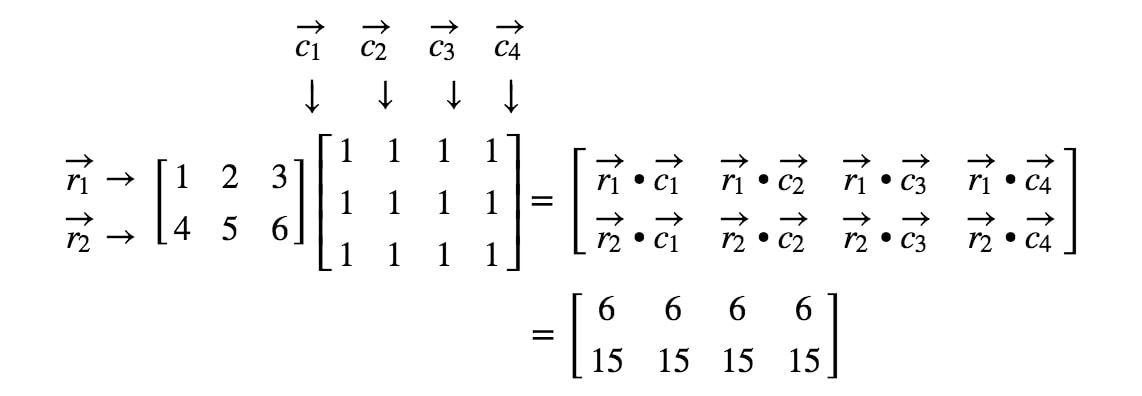
Mitä järkeä oli siis opetella pistepotenttia? No, käytämme pistetuotosta, kun kerromme kaksi matriisia keskenään. Kun kerromme matriisin toisella matriisilla, haluamme käsitellä rivejä ja sarakkeita vektorina. Tarkemmin sanottuna haluamme käsitellä ensimmäisen matriisin jokaista riviä vektorina ja toisen matriisin jokaista saraketta vektorina. Tehdään esimerkki.

Kysymys 3: Etsi A∙BA \bullet BA∙B jos

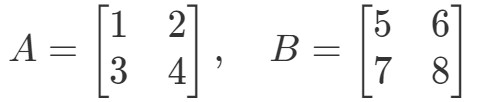
Kummankin matriisin kertominen keskenään antaa tulokseksi:

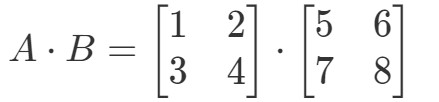
Nyt rivit ja sarakkeet, joihin keskitymme, ovat

jossa r1r_{1}r1 on ensimmäinen rivi, r2r_{2}r2 on toinen rivi ja, c1,c2c_{1}, c_{2}c1,c2 ovat ensimmäinen ja toinen sarake. Nyt käsittelemme jokaista tässä näkemäämme riviä ja saraketta vektorina.

Huomaa tässä, että kertomalla 2 x 2 -matriisi toisella 2 x 2 -matriisilla saadaan 2 x 2 -matriisi. Toisin sanoen saamassamme matriisissa pitäisi olla 4 merkintää.

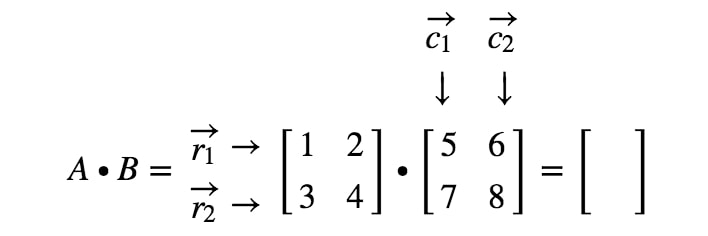
Miten saamme tarkalleen ensimmäisen merkinnän? No, huomaa, että ensimmäinen merkintä sijaitsee ensimmäisellä rivillä ja ensimmäisessä sarakkeessa. Otamme siis yksinkertaisesti r1r_{1}r1:n ja c1c_{1}c1:n pistetuoton. Näin ollen ensimmäinen merkintä on

Miten saamme toisen merkinnän tällä kertaa? No, huomaa, että toisen merkinnän sijainti on ensimmäisellä rivillä ja toisessa sarakkeessa. Otamme siis yksinkertaisesti r1r_{1}r1:n ja c2c_{2}c2:n pistetuoton. Näin ollen toinen merkintä on

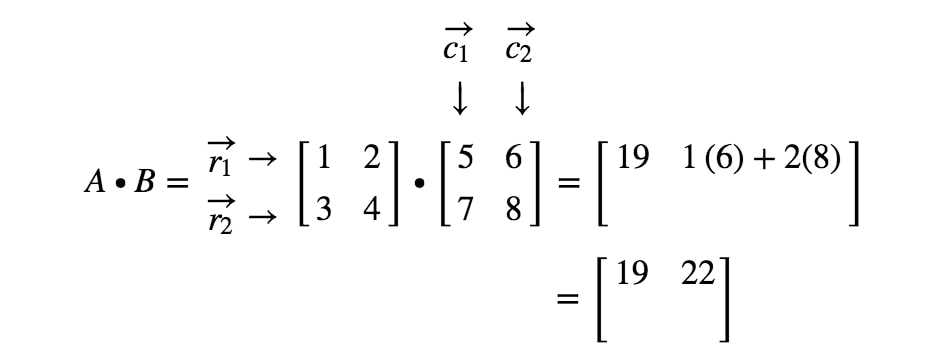
Nyt käytämme samaa strategiaa kahden viimeisen merkinnän etsimiseen. Huomaa, että toiseksi viimeinen merkintä sijaitsee 2nd2^{nd}2. rivillä ja 1st1^{st}1. sarakkeessa, ja viimeinen merkintä sijaitsee 2nd2^{nd}2. rivillä ja 2nd2^{nd}2. sarakkeessa. Otetaan siis r2r_{2}r2:n ja c1c_{1}c1:n pistetuotto ja r2r_{2}r2:n ja c2c_{2}c2:n pistetuotto. Näin saadaan:

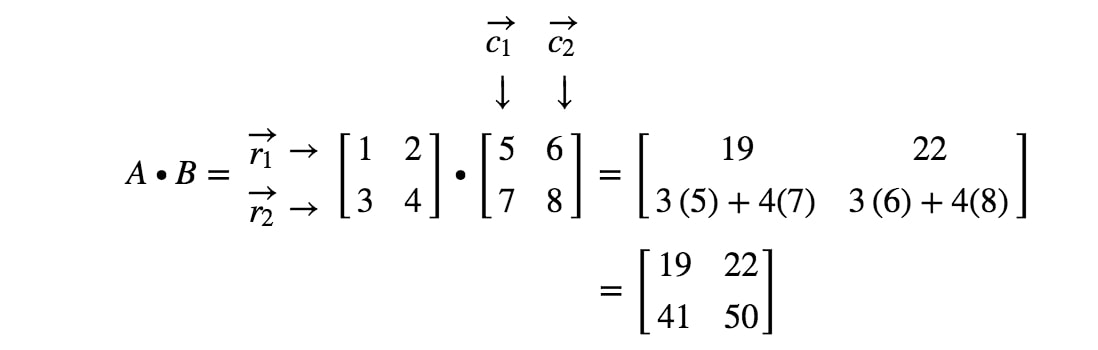
Nyt olemme valmiit! Tämän saamme, kun kerromme 2 x 2 matriisia. Yleensä 2 x 2 -matriisien matriisien kertolaskukaava on

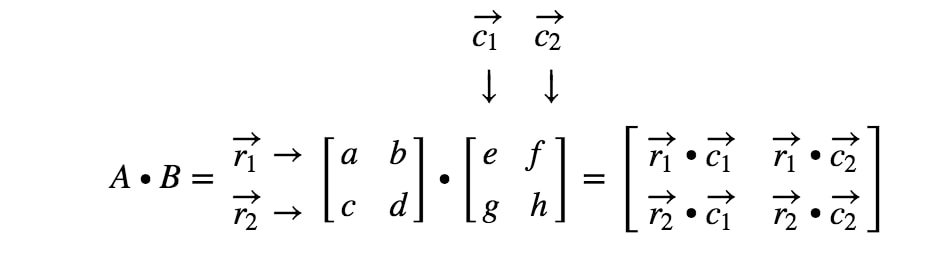
3×3 -matriisien kertolasku

Nyt 3 x 3 -matriisien kertolasku on hyvin samankaltainen prosessi kuin 2 x 2 -matriisien kertolasku. Miksi emme taas tee esimerkkiä matriisikertomuksesta?

Kysymys 4:Etsi A∙BA \bullet BA∙B jos

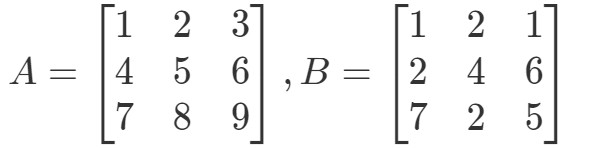
Huomaa ensinnäkin, että kertomalla ne pitäisi saada toinen 3 x 3 matriisi. Toisin sanoen,

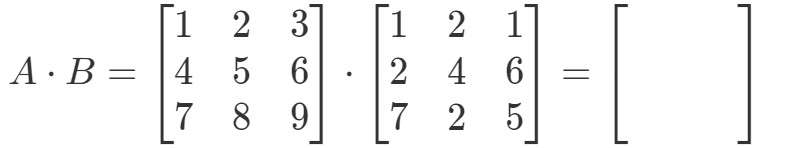
Kirjoitetaan nyt kaikki rivit ensimmäiseen matriisiin ja sarakkeet toiseen matriisiin.

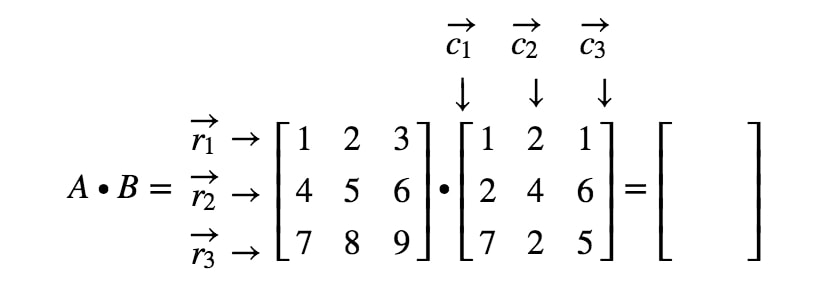
Huomaa, että matriisin ensimmäinen merkintä sijaitsee 1. 1^{st}1. rivillä ja 1. 1^{st}1. sarakkeessa, joten otamme r1r_{1}r1:n ja c1c_{1}c1:n pistetulon. Näin saadaan:

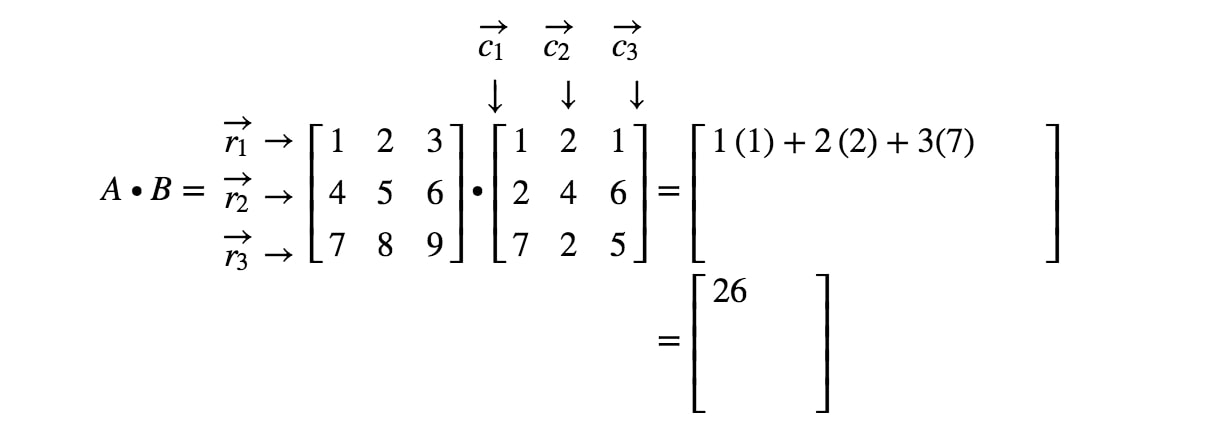
Huomaa nyt, että matriisin toinen merkintä sijaitsee 1.1^{st}1. rivillä ja 2.2^{nd}2. sarakkeessa. Otetaan siis r1r_{1}r1:n ja c2c_{2}c2:n pistetuotto. Näin saadaan:

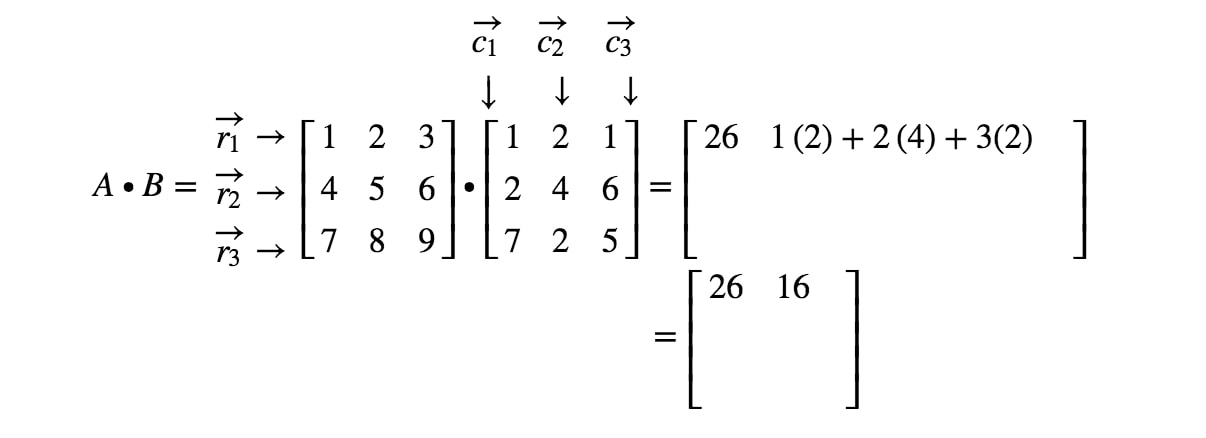
Jos jatkamme kaikkien merkintöjen paikantamista ja teemme rivejä ja sarakkeita vastaavan pistepotentiaalin, niin saamme lopputuloksen.

Olemme valmiit! Huomaa, että mitä suurempia matriisit ovat, sitä työläämmäksi matriisien kertominen käy. Tämä johtuu siitä, että joudumme käsittelemään yhä useampia lukuja! Yleisesti ottaen 3 x 3 -matriisien matriisien kertolaskukaava on

Miten kerrotaan matriisit, joilla on eri mitat?

Tähän mennessä olemme kertoneet matriisit, joilla on samat mitat. Lisäksi tiedämme, että kertomalla kaksi matriisia, joilla on sama ulottuvuus, saadaan samansuuruinen matriisi. Mutta mitä tapahtuu, jos kerromme matriisin, jolla on eri ulottuvuudet? Mistä tietäisimme lasketun matriisin dimensiot? Ensin meidän on nähtävä, että kertomalla matriisit saadaan määritelty matriisi.

Onko matriisi määritelty?

On tapauksia, joissa kahden matriisin kertominen keskenään ei ole mahdollista. Näissä tapauksissa kutsumme matriisia määrittelemättömäksi. Mistä tiedämme, että ne ovat määrittelemättömiä?

Kahden matriisin tulo on määritelty vain, jos ensimmäisen matriisin sarakkeiden lukumäärä on yhtä suuri kuin toisen matriisin rivien lukumäärä.

Kokeillaan käyttää tätä määritelmää tässä esimerkissä.

Kysymys 5: Olkoon

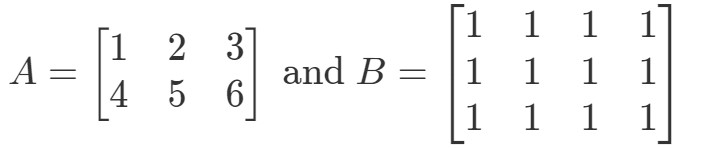
Onko A∙BA \bullet BA∙B määritelty?

Aluksi huomataan, että ensimmäisessä matriisissa on 3 saraketta. Myös toisessa matriisissa on 3 riviä. Koska molemmat ovat yhtä suuria kuin 3, tiedän, että A∙BA \bullet BA∙B on määritelty.

Nyt kun tiedämme, että se on määritelty, mistä tiedämme A∙BA \bullet BA∙B:n mitat?

Dimensio-ominaisuus

Löytääksemme A∙BA \bullet BA∙B:n dimensiot, meidän on ensin tarkasteltava erikseen ja:n dimensioita.

Nyt laitamme matriisien dimensiot vierekkäin näin:

Tehdään nyt niin, että otamme ensimmäisen luvun ja viimeisen luvun ja yhdistelemme ne saadaksemme A∙BA \bulletin BA∙B dimensiot. Katso, että ensimmäinen numero on 2 ja viimeinen numero on 4. Joten A∙BA \bullet BA∙B:n mitat ovat:

Nyt kun tiedämme matriisin mitat, voimme vain laskea jokaisen merkinnän käyttämällä pistepotentiaaleja. Näin saamme:

Nyt kun osaamme hyvin kertoa matriiseja, miksi emme katsoisi joitakin matriisien kertolaskujen sääntöjä?

Matriisien kertolaskujen ominaisuudet

Minkä tyyppisiä ominaisuuksia matriisien kertolaskuilla oikeastaan on? Määritellään ensin muodollisesti kaikki.

Olkoot X,Y,ZX, Y, ZX,Y,Z matriisit, InI_{n}In identiteettimatriisi ja OnO_{n}On nollamatriisi. Jos kaikilla näillä viidellä matriisilla on yhtä suuret mitat, niin meillä on seuraavat matriisien väliset matriisien kertolaskuominaisuudet:

Assosiatiivisen ominaisuuden mukaan kertolaskujärjestyksellä ei ole väliä. Toisin sanoen, laskemalla X∙YX \bullet YX∙Y ja kertomalla sitten ZZZ:llä saat saman tuloksen kuin laskemalla Y∙ZY \bullet ZY∙Z ja kertomalla sitten XXX:llä. Tehdään esimerkki.

Kysymys 6: Osoita, että assosiatiivinen ominaisuus toimii näillä matriiseilla:

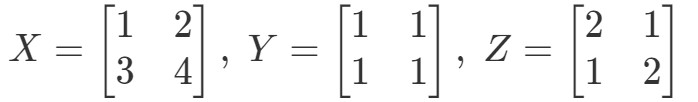
Katsomalla assosiatiivisen ominaisuuden yhtälön vasenta puolta nähdään, että (XY)Z(XY)Z(XY)Z(XY)Z antaa:

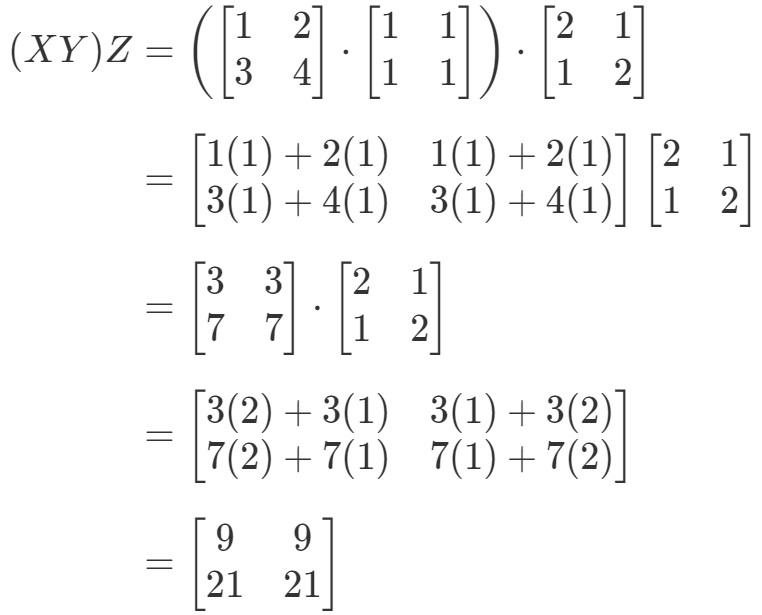
Katsomme nyt yhtälön oikeaa puolta assosiatiivisen ominaisuuden suhteen ja näemme, että X(YZ)X(YZ)X(YZ) antaa:

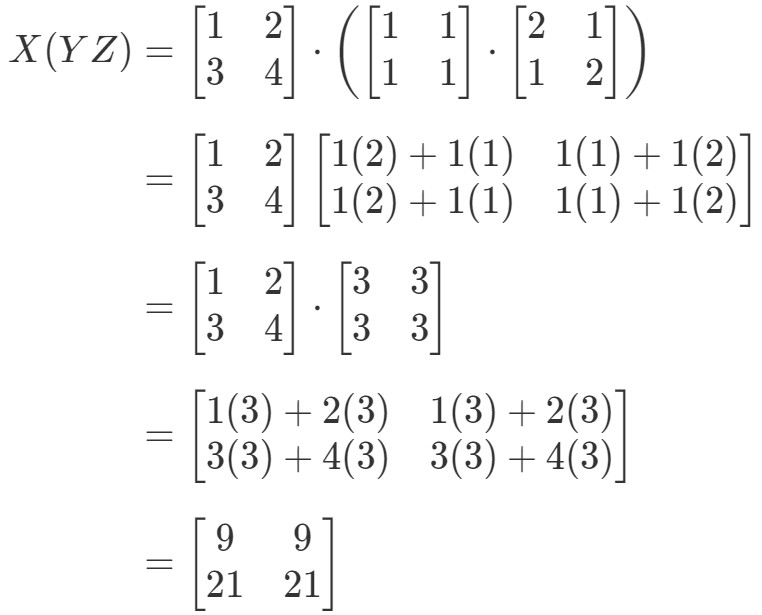
Katso, kuinka yhtälön vasen ja oikea puoli ovat molemmat yhtä suuret. Näin ollen tiedämme, että assosiatiivinen ominaisuus todella toimii! Tämä taas tarkoittaa, että matriisien kertolaskujärjestyksellä ei ole väliä!

Nyt seuraava ominaisuus on distributiivinen ominaisuus. Distributiivinen ominaisuus sanoo, että:

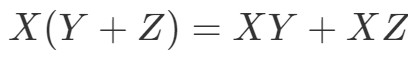
Näemme, että saamme käyttää foliotekniikkaa myös matriiseille. Jotta näemme, että tämä ominaisuus toimii, tehdään esimerkki.

Kysymys 7: Osoita, että distributiivinen ominaisuus toimii seuraaville matriiseille:

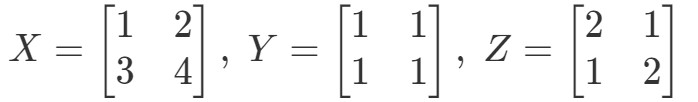
Katsotaan, että yhtälön vasen puoli on X(Y+Z)X(Y + Z)X(Y+Z). Näin ollen laskemalla saadaan:

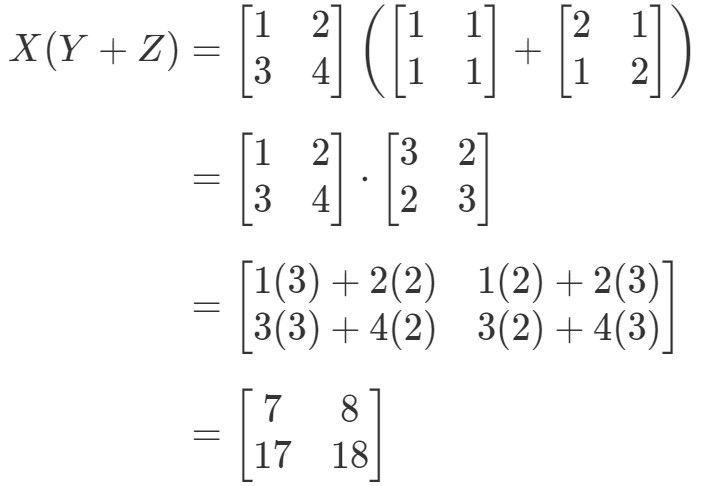
Tarkistetaan nyt, antaako yhtälön oikea puoli täsmälleen saman asian. Huomaa, että yhtälön oikea puoli on XY+XZXY + XZXY+XZ. Tämän laskeminen antaa meille:

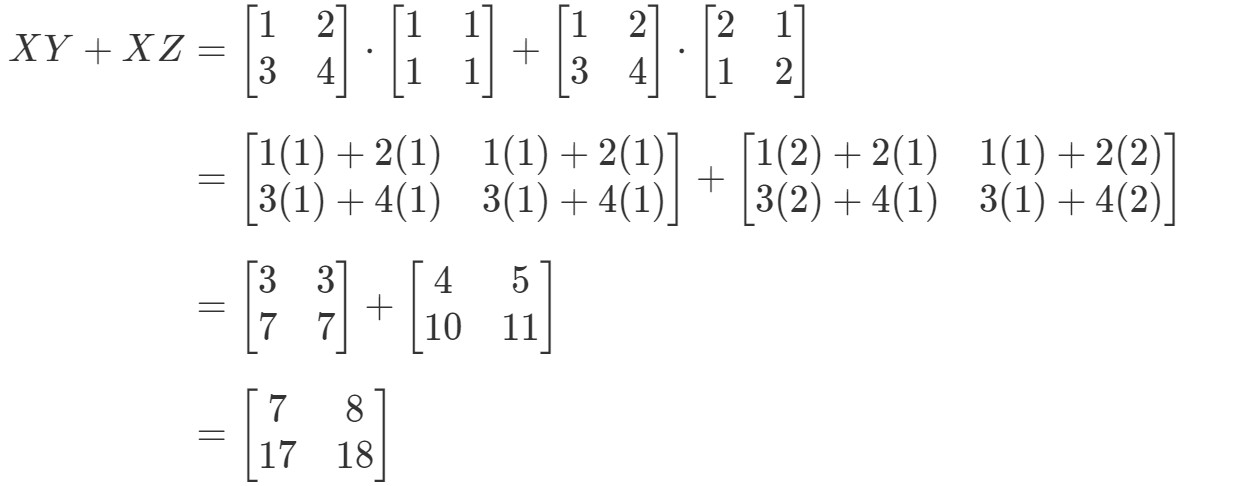
Huomaa, että yhtälön vasen puoli on täsmälleen sama kuin yhtälön oikea puoli. Näin ollen voimme vahvistaa, että distributiivinen ominaisuus todella toimii.

Onko matriisikertolasku kommutatiivinen?

Tiedämme, että matriisikertolasku täyttää sekä assosiatiivisen että distributiivisen ominaisuuden, mutta emme kuitenkaan puhuneet kommutatiivisesta ominaisuudesta lainkaan. Tarkoittaako tämä, että matriisikertolasku ei täytä sitä? Itse asiassa se ei täytä, ja voimme tarkistaa sen esimerkin avulla.

Kysymys 8: Jos matriisikertolasku on kommutatiivinen, niin seuraavan täytyy olla totta:

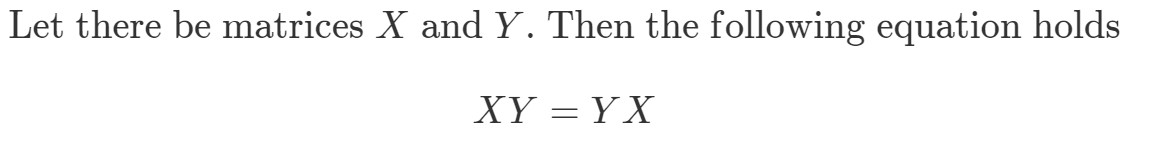
Osoita, että XYeqYXXY eq YXXYeqYX jos

Lasketaan ensin yhtälön vasen puoli. Laskemalla XYXYXY saadaan:

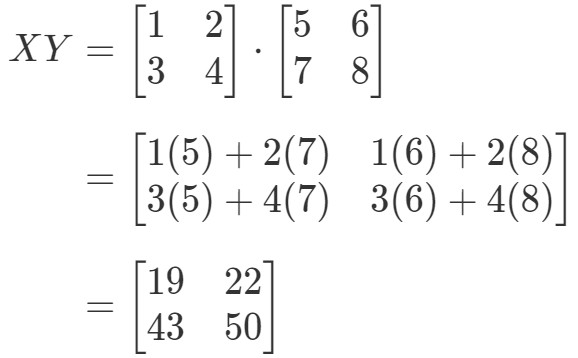
Laskemalla nyt yhtälön oikeanpuoleinen puoli saadaan:

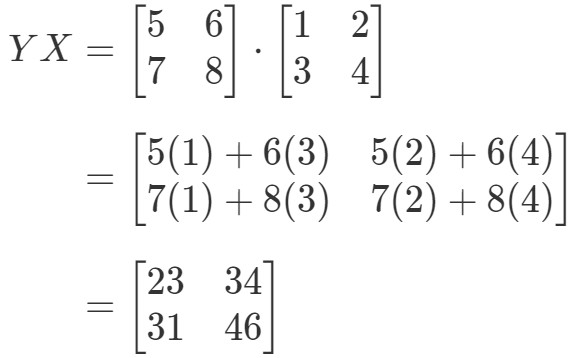
Kuten näet,

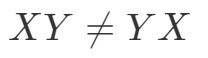
Koska meillä on

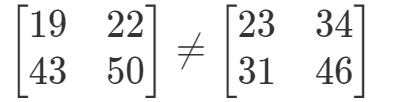
Nämä kaksi matriisia ovat täysin erilaiset.

Nyt on vielä muutama matriisien kertolaskun ominaisuus. Nämä ominaisuudet käsittelevät kuitenkin nolla- ja identtisyysmatriiseja.

Matriisien kertominen nollamatriisille

Matriisien kertomisen ominaisuus nollamatriisille sanoo seuraavaa:

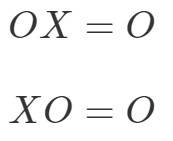
jossa OOO on nollamatriisi.

Tämä tarkoittaa sitä, että jos kerrot nollamatriisin toisella ei-nollamatriisilla, saat nollamatriisin. Testataan, pitääkö tämä paikkansa esimerkin avulla.

Kysymys 9: Osoita, että yhtälö OX=OOX = OOX=O ja XO=OXO = OXO=O pätee, jos:

Katsotaan ensin yhtälöä

Huomaa, että laskemalla OXOXOX saadaan:

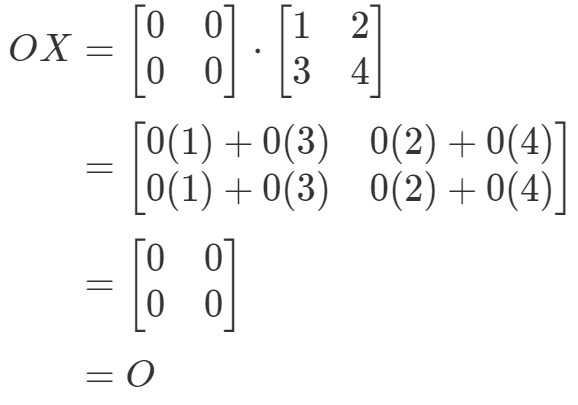
Näemme kyllä, että OX=OOX = OOX=O, joten yhtälö pätee. Vastaavasti, jos laskemme XOXOXO, saamme:

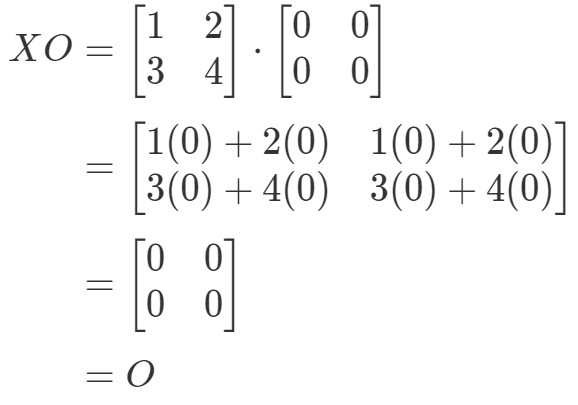
Näemme, että yhtälö XO=OXO = OXO=O pätee, joten olemme valmiit.

Matriisikertolasku identiteettimatriisille

Mutta entäpä matriisikertolaskuominaisuus identiteettimatriiseille? No, ominaisuus sanoo seuraavaa:

jossa InI_{n}In on n×nn \times nn×n identiteettimatriisi. Näemme taas esimerkin avulla, että seuraavat yhtälöt pitävät paikkansa.

Kysymys 10: Osoita, että yhtälöt XI2=XX I_{2} = XXI2=X ja I2X=XI_{2} X = XI2X=X pätee seuraavilla matriiseilla

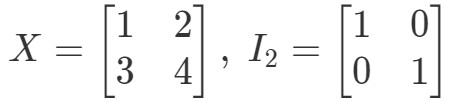
Yhtälölle XI2=XX I_{2} = XXI2=X on siis:

Yhtälö siis pätee. Yhtälön I2X=XI_{2}X = XI2X=X tavoin saadaan:

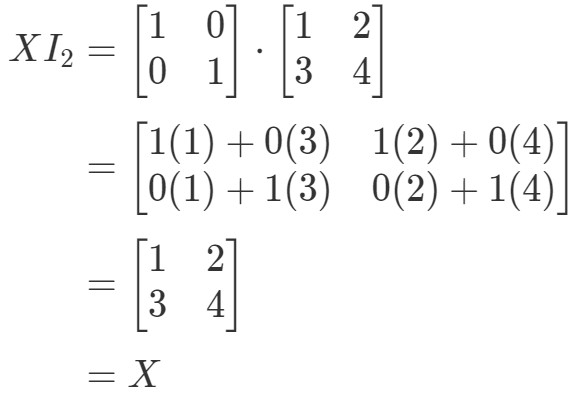
Jälleen yhtälö pätee. Olemme siis valmiit kysymyksen kanssa, ja molemmat yhtälöt pitävät paikkansa. tähän päättyvät kaikki matriisikertolaskennan ominaisuudet. Jos nyt haluat tarkastella matriisikertolaskennan tosielämän sovellusta, suosittelen tutustumaan tähän artikkeliin.

https://www.mathsisfun.com/algebra/matrix-multiplying.html