Free Press

Moltiplicazione di matrici

Ci sono esattamente due modi di moltiplicare matrici. Il primo modo è moltiplicare una matrice con uno scalare. Questo è noto come moltiplicazione scalare. Il secondo modo è moltiplicare una matrice con un’altra matrice. Questo è noto come moltiplicazione matriciale.

Moltiplicazione scalare

la moltiplicazione scalare è in realtà un’operazione matriciale molto semplice. Per moltiplicare uno scalare con una matrice, prendiamo semplicemente lo scalare e lo moltiplichiamo per ogni voce della matrice. Facciamo un esempio.

Domanda 1: Calcola 2A2A2A se

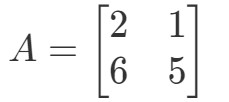
La domanda ci chiede di scoprire cosa sia 2A2A2A. In altre parole, stiamo trovando

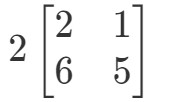
Nota che se dobbiamo moltiplicare 2 ad ogni entrata della matrice, otteniamo che:

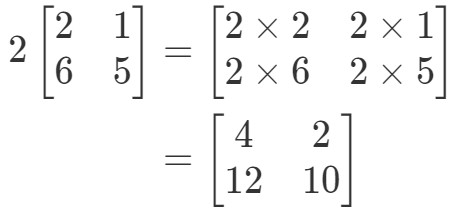
Molto semplice! Facciamone un’altra.

Questione 2: Calcola 0A0A0A se

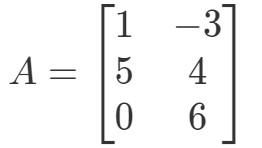
Di nuovo, stiamo cercando di trovare 0A0A0A0A. Questo significa che cercheremo la risposta a

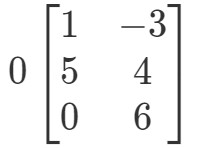
La matrice avrà una forma strana, ma il concetto rimane lo stesso. Moltiplicheremo ancora lo scalare 0 ad ogni voce della matrice. Facendo così otteniamo:

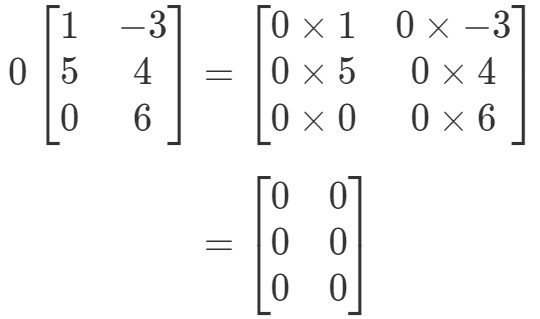
Notate che tutte le voci della matrice sono 0. Questa è conosciuta come una matrice zero che è 3 x 2.

Ora che abbiamo molta familiarità con la moltiplicazione scalare, perché non passiamo alla moltiplicazione di matrice?

Come moltiplicare le matrici

Per moltiplicare una matrice per un’altra matrice, dobbiamo prima imparare cos’è il prodotto di punti.

Cos’è il prodotto di punti?

Il prodotto di punti (noto anche come moltiplicazione vettoriale) è un modo per calcolare il prodotto di due vettori. Per esempio, facciamo che i due vettori siano:

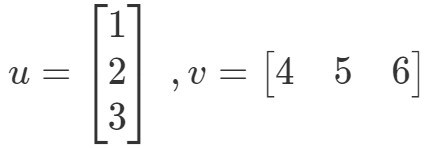
Come potrei moltiplicare questi due vettori? Semplicemente moltiplicando le voci corrispondenti e sommando i prodotti. In altre parole,

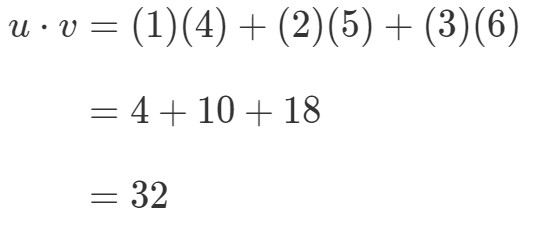
Così otteniamo un unico valore dalla moltiplicazione dei vettori. Tuttavia, si noti che i due vettori hanno lo stesso numero di voci; e se uno dei vettori ha un numero di voci diverso dall’altro? Per esempio, lasciamo che

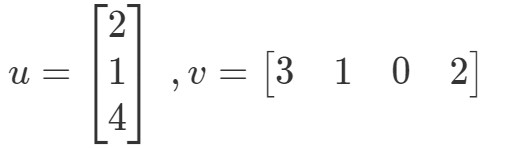
Se dovessi moltiplicare le voci corrispondenti e sommarle tutte insieme, allora otterrei:

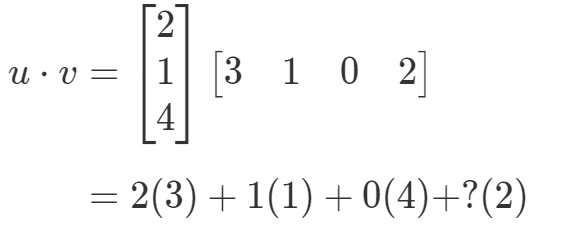
C’è un problema qui. Le prime tre voci hanno voci corrispondenti con cui moltiplicare, ma l’ultima voce no. Quindi cosa facciamo qui? La risposta è che non possiamo fare nulla qui. Questo significa semplicemente che non possiamo calcolare il prodotto di punti di questi due vettori.

Quindi, in conclusione, non possiamo trovare il prodotto di punti di due vettori che hanno un numero diverso di voci. Devono avere lo stesso numero di voci.

Moltiplicazione di matrici 2 x 2

Allora a cosa è servito imparare il prodotto di punti? Bene, useremo il prodotto di punti quando moltiplichiamo due matrici insieme. Quando moltiplichiamo una matrice con un’altra matrice, vogliamo trattare le righe e le colonne come un vettore. Più specificamente, vogliamo trattare ogni riga della prima matrice come vettori e ogni colonna della seconda matrice come vettori. Facciamo un esempio.

Questione 3: Trovare A∙BA \bullet BA∙B se

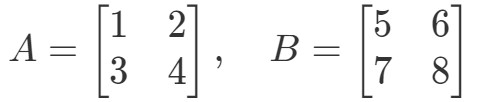
Moltiplicando le due matrici avremo:

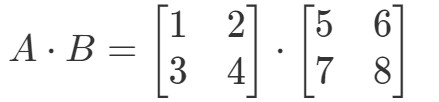
Ora le righe e le colonne su cui ci stiamo concentrando sono

dove r1r_{1}r1 è la prima riga, r2r_{2}r2 è la seconda riga, e, c1,c2c_{1}, c_{2}c1,c2 sono prima e seconda colonna. Ora tratteremo ogni riga e colonna che vediamo qui come un vettore.

Nota qui che moltiplicando una matrice 2 x 2 con un’altra matrice 2 x 2 si ottiene una matrice 2 x 2. In altre parole, la matrice che otteniamo dovrebbe avere 4 voci.

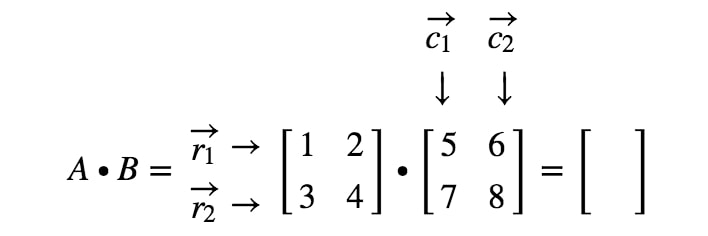
Come otteniamo esattamente la prima voce? Bene, notate che la prima voce si trova sulla prima riga e sulla prima colonna. Quindi prendiamo semplicemente il prodotto di punti di r1r_{1}r1 e c1c_{1}c1. Così, la prima voce sarà

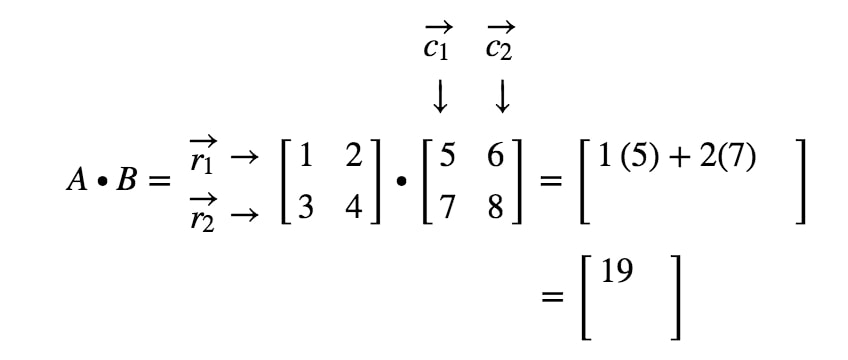
Come otteniamo la seconda voce questa volta? Bene, notate che la posizione della seconda voce è nella prima riga e nella seconda colonna. Quindi prendiamo semplicemente il prodotto di punti di r1r_{1}r1 e c2c_{2}c2. Così, la seconda voce sarà

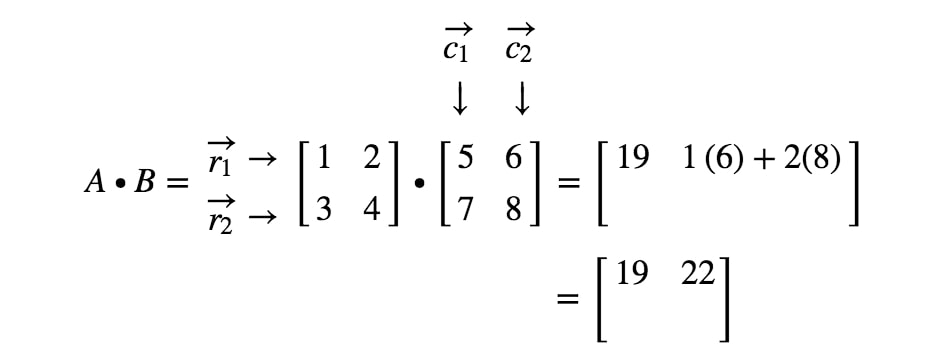
Ora useremo la stessa strategia per cercare le ultime due voci. Notate che la penultima voce si trova nella 2^{nd}2^ riga e 1^{st}1^ colonna, e l’ultima voce si trova nella 2^{nd}2^ riga e 2^{nd}2^ colonna. Quindi prendiamo il prodotto di punti di r2r_{2}r2 e c1c_{1}c1, e il prodotto di punti di r2r_{2}r2 e c2c_{2}c2. Questo ci dà:

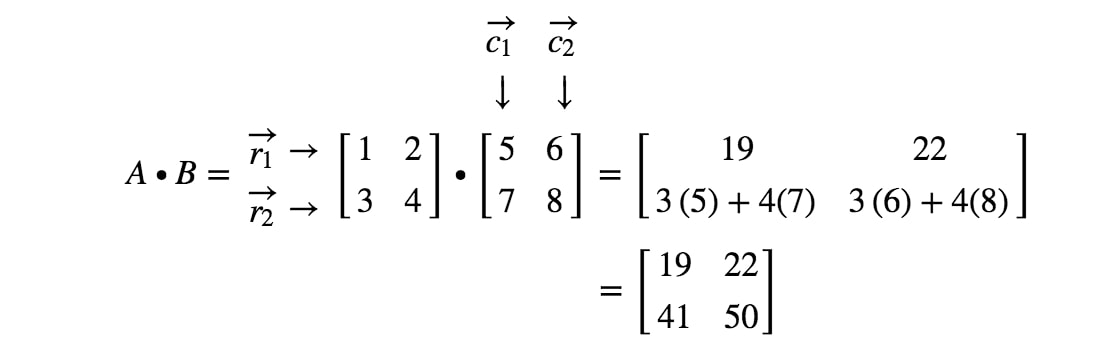
Ora abbiamo finito! Questo è ciò che otteniamo quando moltiplichiamo 2 x 2 matrici. In generale, la formula di moltiplicazione di matrici 2 x 2 è

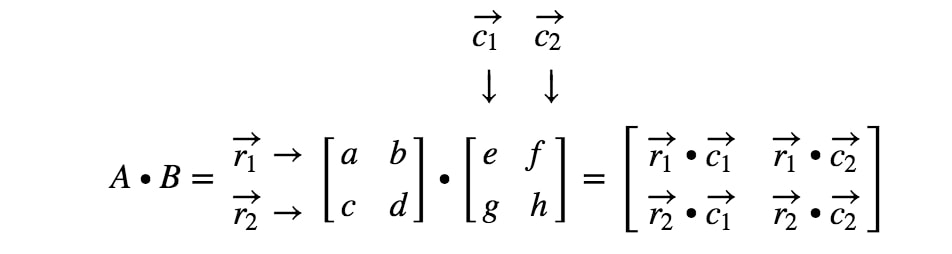
Moltiplicazione di matrici 3 x 3

Ora il processo di moltiplicazione di una matrice 3 x 3 è molto simile a quello di una matrice 2 x 2. Di nuovo, perché non facciamo un esempio di moltiplicazione di matrice?

Domanda 4:Trova A∙BA ∙B se

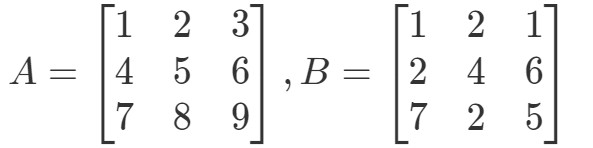
Prima di tutto, nota che moltiplicandoli dovremmo avere un’altra matrice 3 x 3. In altre parole,

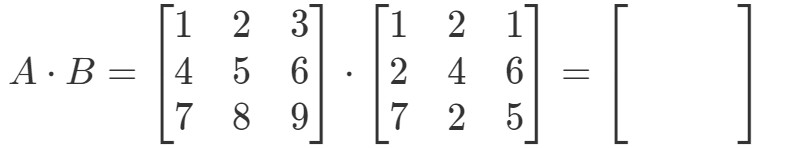
Ora etichettiamo tutte le nostre righe nella prima matrice e le colonne nella seconda matrice.

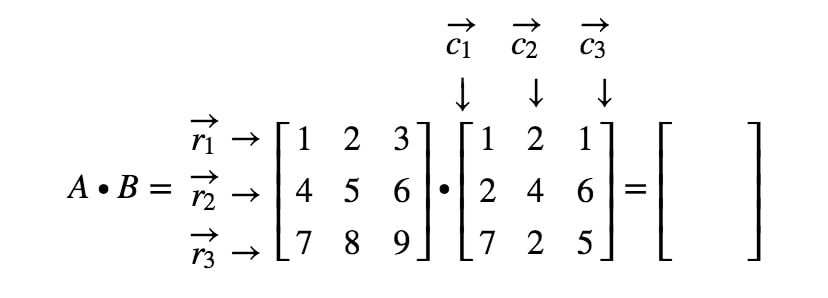
Nota che la prima voce della matrice si trova nella 1^{st}1^ riga e 1^{st}1^ colonna, quindi prendiamo il prodotto di punti di r1r_{1}r1 e c1c_{1}c1. Questo ci dà:

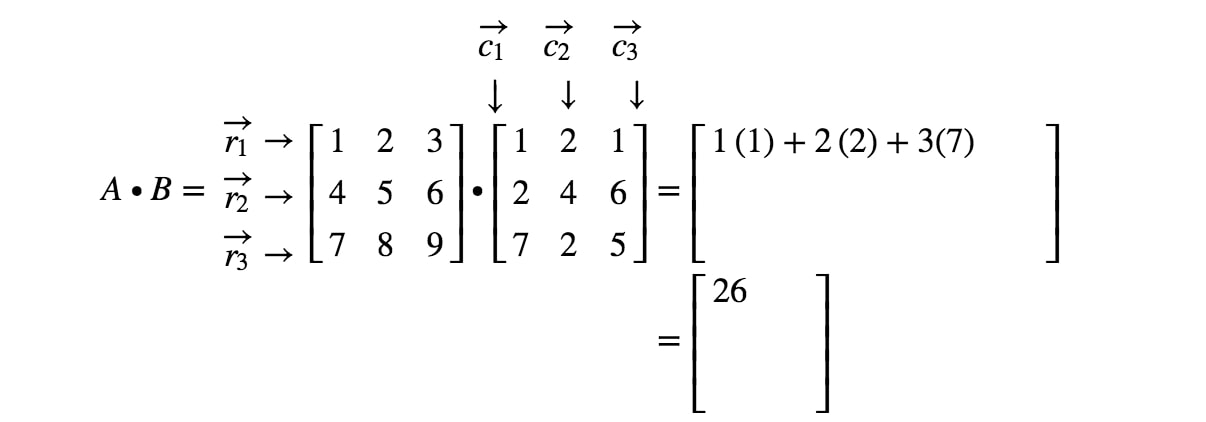
Ora notate che la seconda voce della matrice si trova nella 1^{st}1^ riga e 2^{nd}2^ colonna. Quindi, prendiamo il prodotto di punto di r1r_{1}r1 e c2c_{2}c2. Questo ci dà:

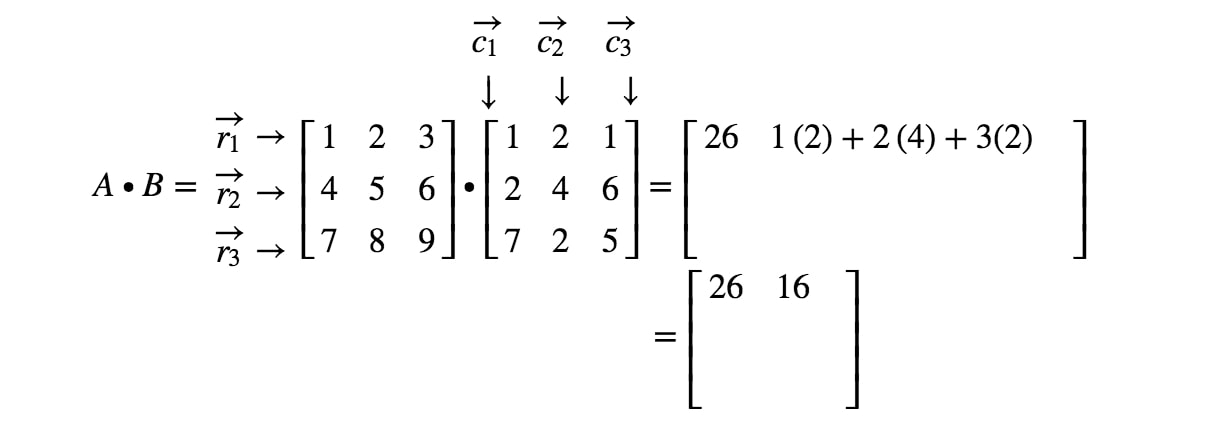
Se dobbiamo continuare a localizzare tutte le voci e fare il prodotto di punti corrispondente alle righe e alle colonne, allora otteniamo il risultato finale.

Abbiamo finito! Notate che più grandi sono le matrici, più noiosa diventa la moltiplicazione di matrici. Questo perché abbiamo a che fare con sempre più numeri! In generale, la formula di moltiplicazione di matrici 3 x 3 è

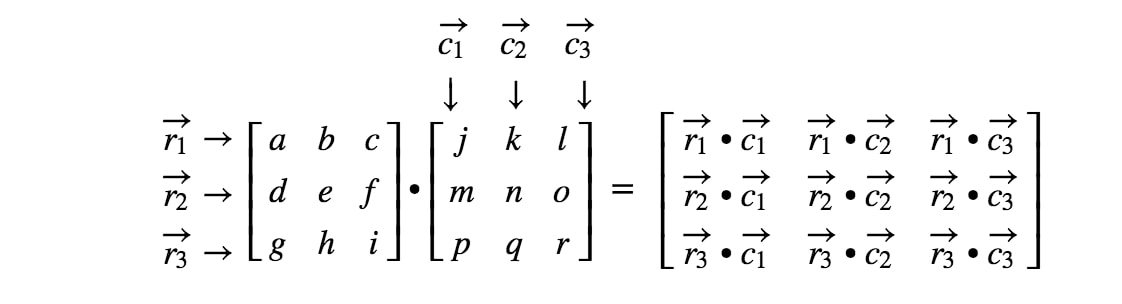
Come moltiplicare matrici con dimensioni diverse?

Finora abbiamo moltiplicato matrici con le stesse dimensioni. Inoltre, sappiamo che moltiplicando due matrici con la stessa dimensione si ottiene una matrice delle stesse dimensioni. Ma cosa succede se moltiplichiamo una matrice con dimensioni diverse? Come potremmo conoscere le dimensioni della matrice calcolata? Per prima cosa, dobbiamo vedere che moltiplicando le matrici si ottiene una matrice definita.

La matrice è definita?

Ci sono casi in cui non è possibile moltiplicare insieme due matrici. Per questi casi, chiamiamo la matrice ad essere indefinita. Come possiamo dire se sono indefinite?

Il prodotto di due matrici è definito solo se il numero di colonne della prima matrice è uguale al numero di righe della seconda matrice.

Provo a usare questa definizione in questo esempio.

Questione 5: Facciamo

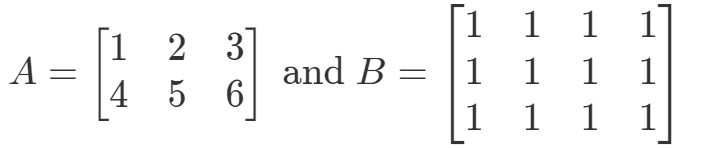
È A∙BA ∙BA ∙B definito?

Prima di tutto, nota che la prima matrice ha 3 colonne. Inoltre, la seconda matrice ha 3 righe. Dato che sono entrambe uguali a 3, allora so che A∙BA \bullet BA∙B è definito.

Ora che sappiamo che è definito, come potremmo sapere le dimensioni di A∙BA \bullet BA∙B?

La proprietà delle dimensioni

Per trovare le dimensioni di A∙BA \bullet BA∙B, dobbiamo prima guardare le dimensioni di e separatamente.

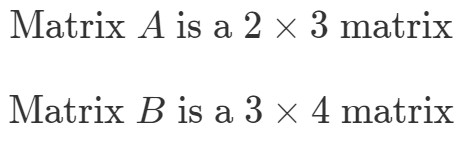
Ora metteremo le dimensioni delle matrici una accanto all’altra in questo modo:

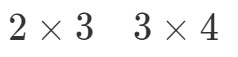
Quello che faremo ora è prendere il primo numero e l’ultimo numero e combinarli per ottenere le dimensioni di A∙BA \bullet BA∙B. Vedete che il primo numero è 2 e l’ultimo numero è 4. Quindi le dimensioni di A∙BA \bullet BA∙B saranno:

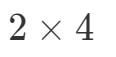
Ora che conosciamo le dimensioni della matrice, possiamo semplicemente calcolare ogni voce usando i prodotti dei punti. Questo ci darà:

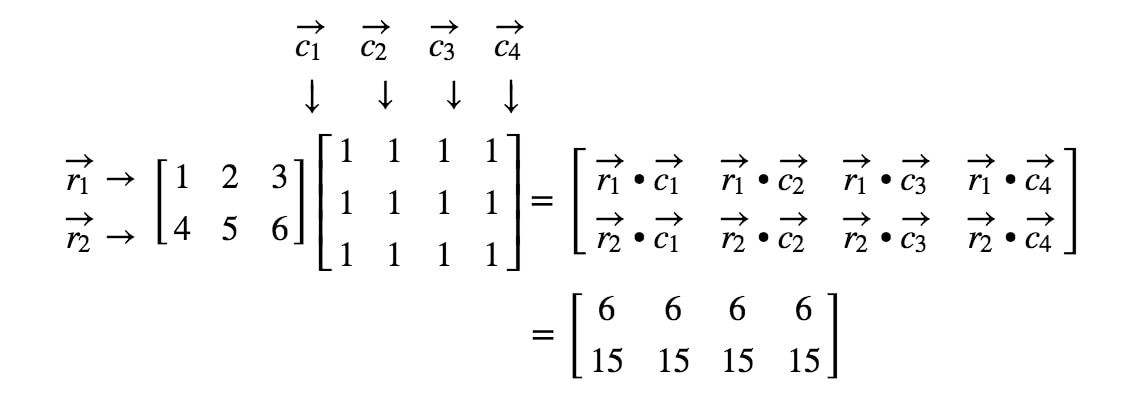
Ora che sappiamo come moltiplicare matrici molto bene, perché non diamo un’occhiata ad alcune regole di moltiplicazione delle matrici? Prima di tutto, definiamo formalmente il tutto.

Lasciamo che X,Y,ZX, Y, ZX,Y,Z siano matrici, InI_{n}In sia una matrice di identità, e OnO_{n}On sia una matrice zero. Se tutte e cinque queste matrici hanno dimensioni uguali, allora avremo le seguenti proprietà di moltiplicazione matrice-matrice:

La proprietà associativa afferma che l’ordine in cui si moltiplica non ha importanza. In altre parole, calcolando X∙YX \bullet YX∙Y e poi moltiplicando con ZZZ si ottiene lo stesso risultato che calcolando Y∙ZY \bullet ZY∙Z e poi moltiplicando con XXX. Facciamo un esempio.

Questione 6: Mostrare che la proprietà associativa funziona con queste matrici:

Guardando il lato sinistro dell’equazione nella proprietà associativa, vediamo che (XY)Z(XY)Z(XY)Z dà:

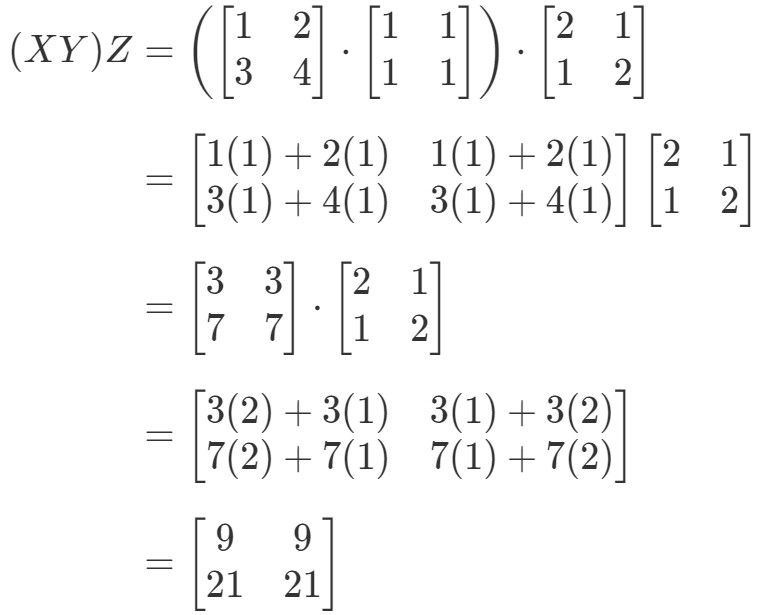
Ora guardando il lato destro dell’equazione nella proprietà associativa, vediamo che X(YZ)X(YZ)X(YZ) dà:

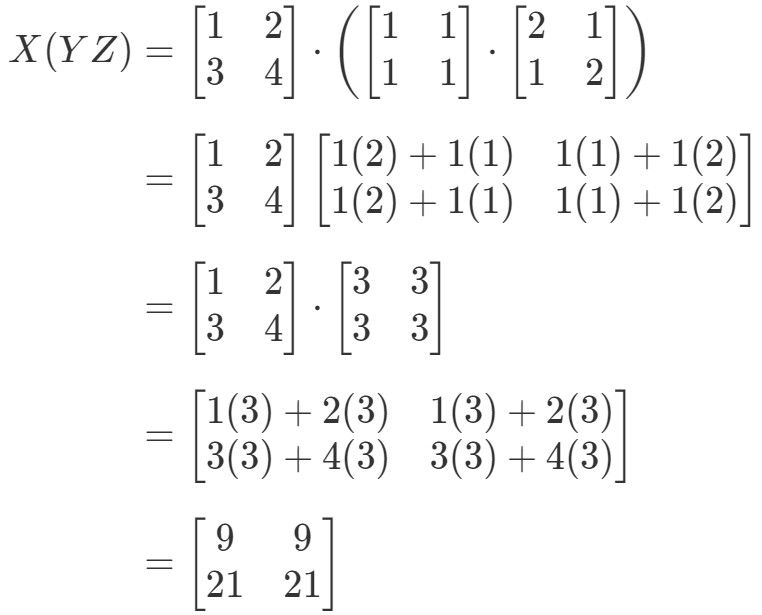
Vedi come il lato sinistro e quello destro dell’equazione sono entrambi uguali. Quindi, sappiamo che la proprietà associativa funziona davvero! Di nuovo, questo significa che l’ordine di moltiplicazione delle matrici non ha importanza!

Ora la prossima proprietà è la proprietà distributiva. La proprietà distributiva afferma che:

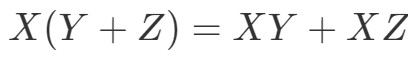
Vediamo che possiamo usare la tecnica del fioretto anche per le matrici. Solo per mostrare che questa proprietà funziona, facciamo un esempio.

Questione 7: Mostrare che la proprietà distributiva funziona per le seguenti matrici:

Vedi che il lato sinistro dell’equazione è X(Y+Z)X(Y + Z)X(Y + Z). Quindi calcolando questo ci dà:

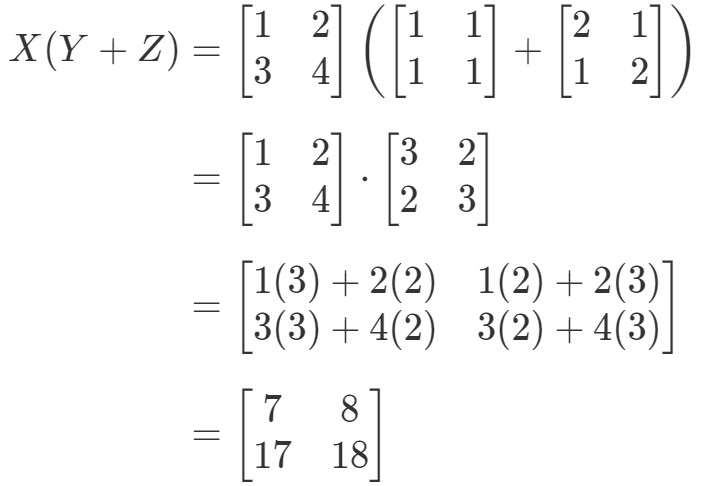
Ora controlliamo se il lato destro dell’equazione ci dà esattamente la stessa cosa. Notate che il lato destro dell’equazione è XY+XZXY + XZXY+XZ. Calcolando questo ci dà:

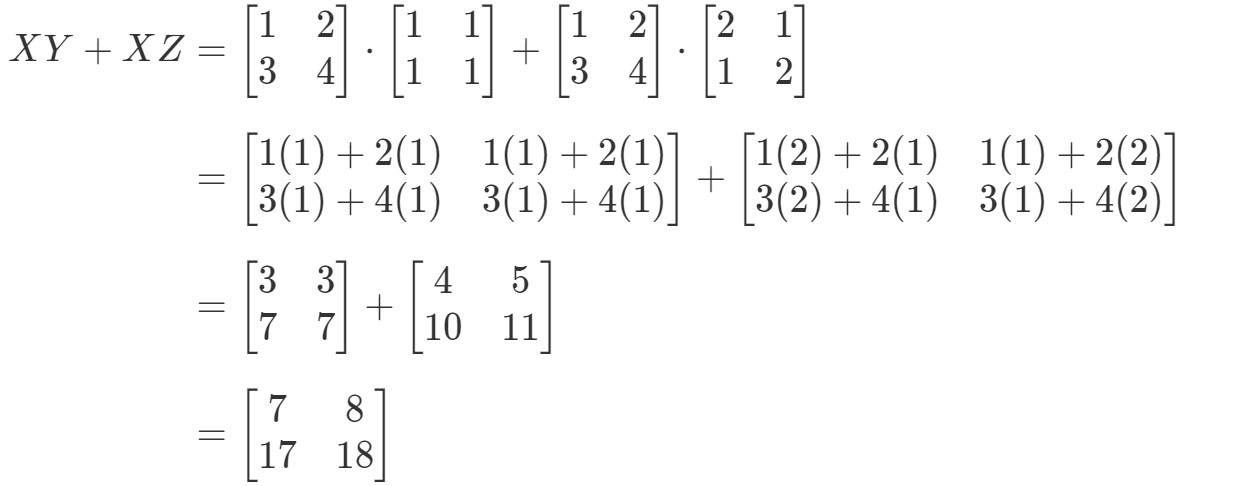
Nota che il lato sinistro dell’equazione è esattamente uguale al lato destro dell’equazione. Quindi, possiamo confermare che la proprietà distributiva funziona davvero.

La moltiplicazione di matrici è commutativa?

Sappiamo che la moltiplicazione di matrici soddisfa entrambe le proprietà associativa e distributiva, tuttavia non abbiamo parlato affatto della proprietà commutativa. Questo significa che la moltiplicazione di matrici non la soddisfa? In realtà no, e possiamo verificarlo con un esempio.

Domanda 8: Se la moltiplicazione di matrici è commutativa, allora deve essere vero quanto segue:

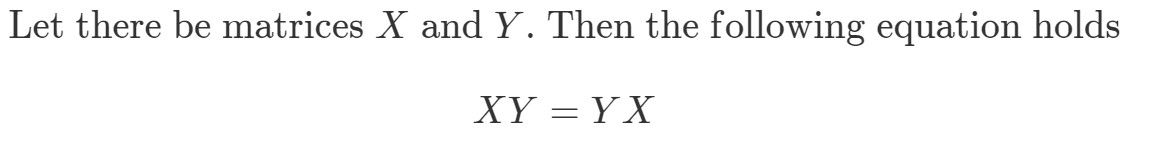
Si dimostri che XYeqYXXY eq YXXYeqYX se

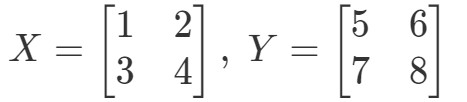
Prima calcoliamo il lato sinistro dell’equazione. Calcolando XYXYXY ci dà:

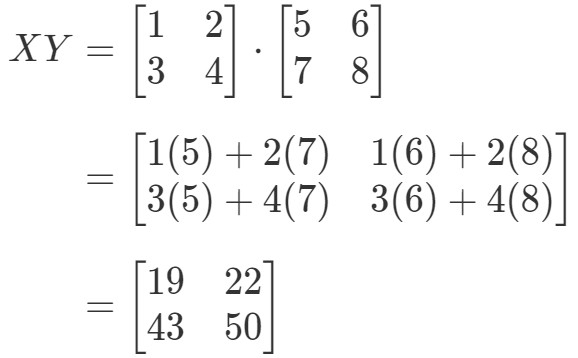
Ora calcolando il lato destro dell’equazione, abbiamo:

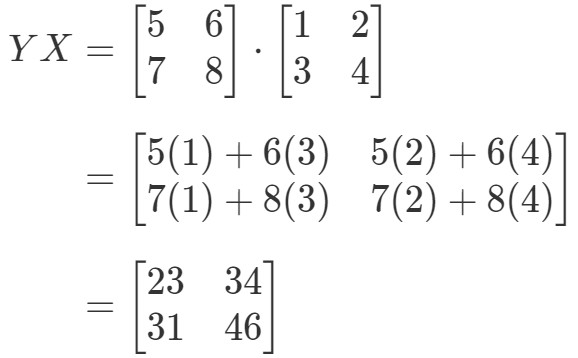
Come potete vedere,

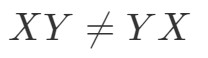
Perché abbiamo

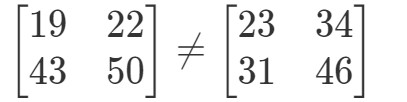
Queste due matrici sono completamente diverse.

Ora ci sono ancora alcune proprietà della moltiplicazione di matrici. Tuttavia, queste proprietà riguardano le matrici zero e identità.

Moltiplicazione della matrice per la matrice zero

La proprietà di moltiplicazione della matrice per la matrice zero afferma quanto segue:

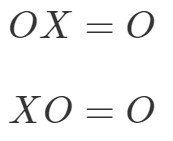
dove OOO è una matrice zero.

Questo significa che se si dovesse moltiplicare una matrice zero con un’altra matrice non zero, allora si otterrebbe una matrice zero. Verifichiamo se questo è vero con un esempio.

Questione 9: Mostrare che l’equazione OX=OOX = OOX=O e XO=OXO = OXO=O vale se:

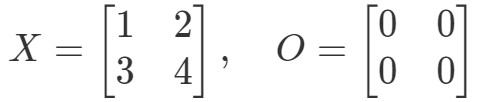
Guardiamo prima l’equazione

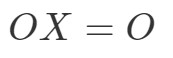
Si noti che calcolando OXOXOX si ottiene:

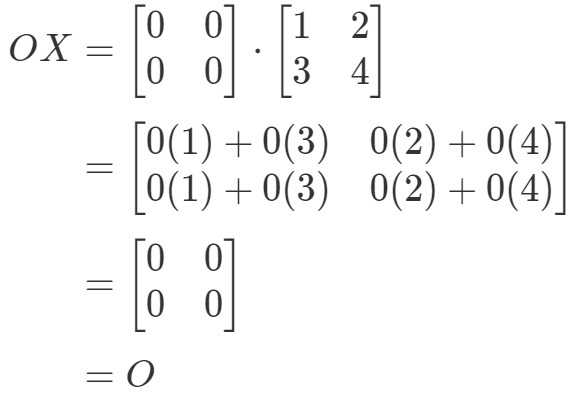
Vediamo che OX=OOX = OOX=O, quindi l’equazione vale. Allo stesso modo, se calcoliamo XOXOXO, otteniamo:

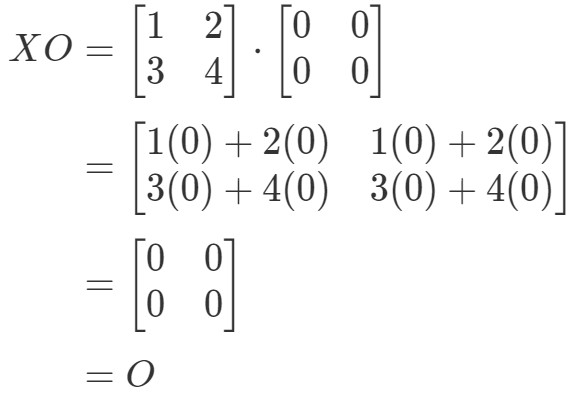
Vediamo che l’equazione XO=OXO = OXO=O vale, quindi abbiamo finito.

Moltiplicazione della matrice per la matrice identità

Ora che ne è della proprietà di moltiplicazione della matrice per le matrici identità? Bene, la proprietà afferma quanto segue:

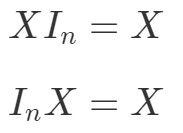
dove InI_{n}In è una matrice identità n×nn \volte nn×n. Di nuovo, possiamo vedere che le seguenti equazioni sono valide con un esempio.

Questione 10: Mostrare che le equazioni XI2=XX I_{2} = XXI2=X e I2X=XI_{2} X = XI2X=X vale con le seguenti matrici

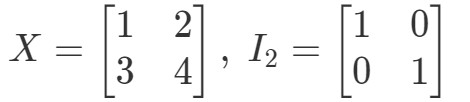
Quindi per l’equazione XI2=XX I_{2} = XXI2=X, abbiamo:

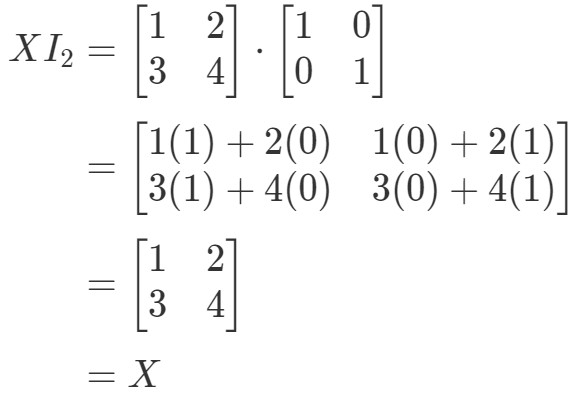
Quindi l’equazione vale. Simile all’equazione I2X=XI_{2}X = XI2X=X, abbiamo:

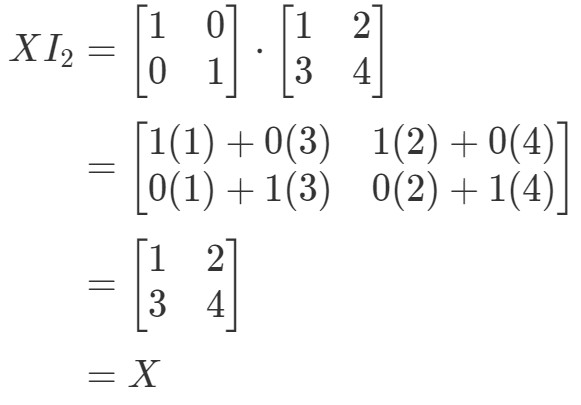
Di nuovo, l’equazione regge. Quindi abbiamo finito con la domanda, ed entrambe le equazioni sono valide. Questo conclude tutte le proprietà della moltiplicazione di matrici. Ora, se volete vedere un’applicazione di vita reale della moltiplicazione di matrici, vi consiglio di guardare questo articolo.

https://www.mathsisfun.com/algebra/matrix-multiplying.html