Free Press

Matrixmultiplikation

Der er præcis to måder at gange matricer på. Den første måde er at multiplicere en matrix med en skalar. Dette er kendt som skalar-multiplikation. Den anden måde er at multiplicere en matrix med en anden matrix. Det er kendt som matrixmultiplikation.

Skalarmultiplikation

Skalarmultiplikation er faktisk en meget simpel matrixoperation. For at multiplicere en skalar med en matrix tager vi simpelthen skalaren og multiplicerer den med hver post i matrixen. Lad os lave et eksempel.

Spørgsmål 1: Beregn 2A2A2A hvis

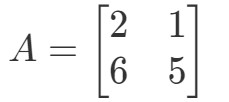
Spørgsmålet beder os om at finde ud af, hvad 2A2A2A er. Med andre ord skal vi finde

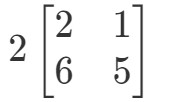
Bemærk, at hvis vi skal gange 2 til hver post i matricen, får vi det:

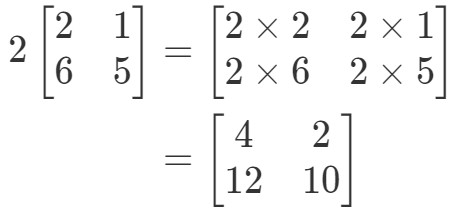
Meget simpelt! Lad os lave endnu en.

Spørgsmål 2: Beregn 0A0A0A hvis

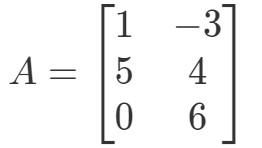
Også her forsøger vi at finde 0A0A0A0A. Det betyder, at vi skal lede efter svaret på

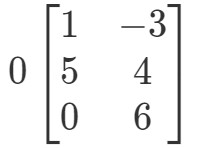
Matrixen vil være mærkeligt formet, men konceptet forbliver det samme. Vi vil stadig gange skalaren 0 til hver post i matricen. Gør vi det, får vi:

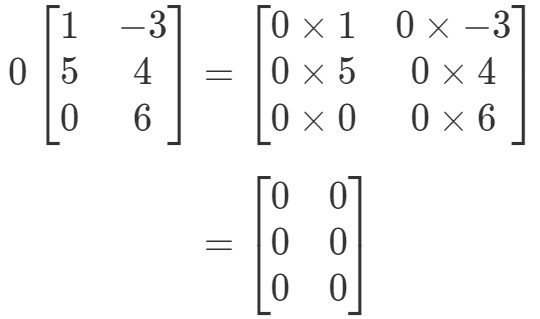
Bemærk, at alle poster i matricen er 0. Dette er kendt som en nulmatrix, der er 3 x 2.

Nu hvor vi er meget fortrolige med skalar multiplikation, hvorfor går vi så ikke videre til matrixmultiplikation?

Sådan multiplicerer vi matricer

For at multiplicere en matrix med en anden matrix skal vi først lære, hvad punktprodukt er.

Hvad er punktprodukt?

Punktprodukt (også kendt som vektormultiplikation) er en måde at beregne produktet af to vektorer på. Lad for eksempel de to vektorer være:

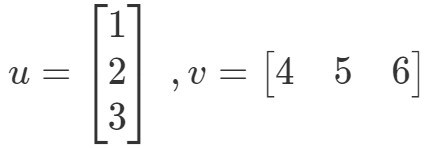
Hvordan vil jeg gange disse to vektorer? Du skal blot gange de tilsvarende poster, og lægge produkterne sammen. Med andre ord,

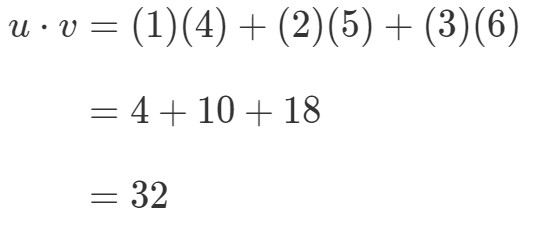
Sådan får vi en enkelt værdi ved at gange vektorerne. Læg dog mærke til, at de to vektorer har det samme antal poster, men hvad nu hvis den ene af vektorerne har et andet antal poster end den anden? Lad for eksempel

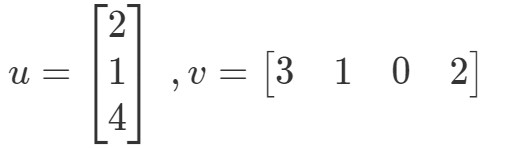
Hvis jeg skulle gange de tilsvarende poster og lægge dem alle sammen sammen, så får jeg:

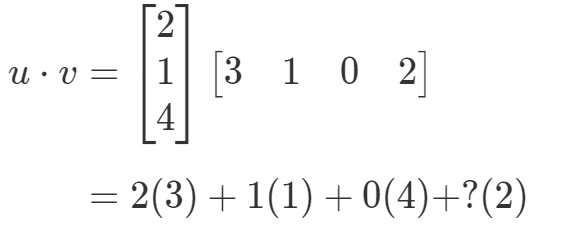
Der er et problem her. De tre første poster har tilsvarende poster at gange med, men det har den sidste post ikke. Så hvad gør vi her? Svaret er, at vi ikke kan gøre noget her. Det betyder blot, at vi ikke kan beregne prikproduktet af disse to vektorer.

Så afslutningsvis kan vi ikke finde prikproduktet af to vektorer, der har forskellige antal poster. De skal have det samme antal poster.

2 x 2 Matrixmultiplikation

Så hvad var pointen med at lære punktproduktet? Jo, vi skal bruge prikproduktet, når vi multiplicerer to matricer sammen. Når vi multiplicerer en matrix med en anden matrix, ønsker vi at behandle rækker og kolonner som en vektor. Mere specifikt ønsker vi at behandle hver række i den første matrix som vektorer, og hver kolonne i den anden matrix som vektorer. Lad os lave et eksempel.

Spørgsmål 3: Find A∙BA \bullet BA∙B if

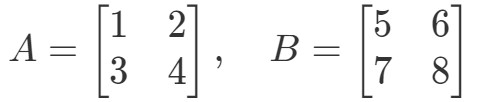
Multiplikation af de to matricer vil give os:

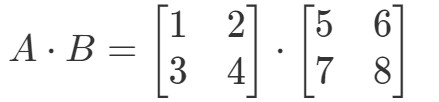
Nu er de rækker og de kolonner vi fokuserer på

hvor r1r_{1}r1 er den første række, r2r_{2}r2 er den anden række, og, c1,c2c_{1}, c_{2}c1,c2 er første og anden kolonne. Nu vil vi behandle hver række og kolonne, vi ser her, som en vektor.

Bemærk her, at multiplikation af en 2 x 2-matrix med en anden 2 x 2-matrix giver en 2 x 2-matrix. Med andre ord skal den matrix, vi får, have 4 poster.

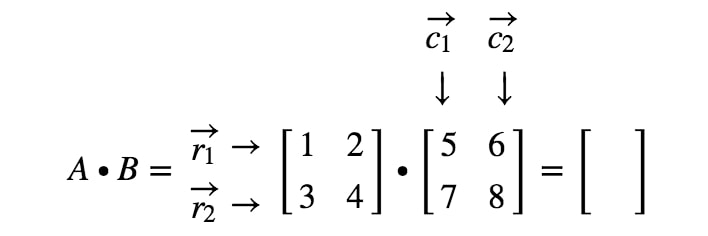
Hvordan får vi præcist den første post? Jo, læg mærke til, at den første post ligger på den første række og første kolonne. Så vi tager simpelthen prikproduktet af r1r_{1}r1 og c1c_{1}c1. Således vil den første post være

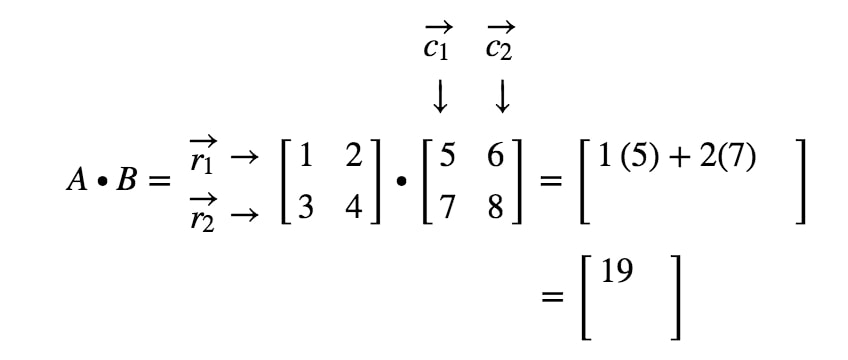
Hvordan får vi den anden post denne gang? Jo, bemærk, at placeringen af den anden post er i den første række og anden kolonne. Så vi tager simpelthen prikproduktet af r1r_{1}r1 og c2c_{2}c2. Således vil den anden post være

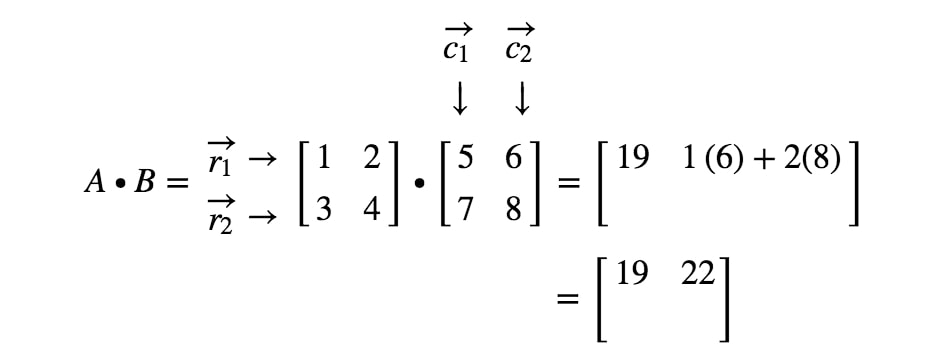
Nu skal vi bruge den samme strategi til at lede efter de to sidste poster. Bemærk, at den næstsidste post er placeret i 2nd2^{nd}2nd række og 1st1^{st}1st kolonne, og at den sidste post er placeret i 2nd2^{nd}2nd række og 2nd2^{nd}2nd kolonne. Så vi tager prikproduktet af r2r_{2}r2 og c1c_{1}c1, og prikproduktet af r2r_{2}r2 og c2c_{2}c2. Dette giver os:

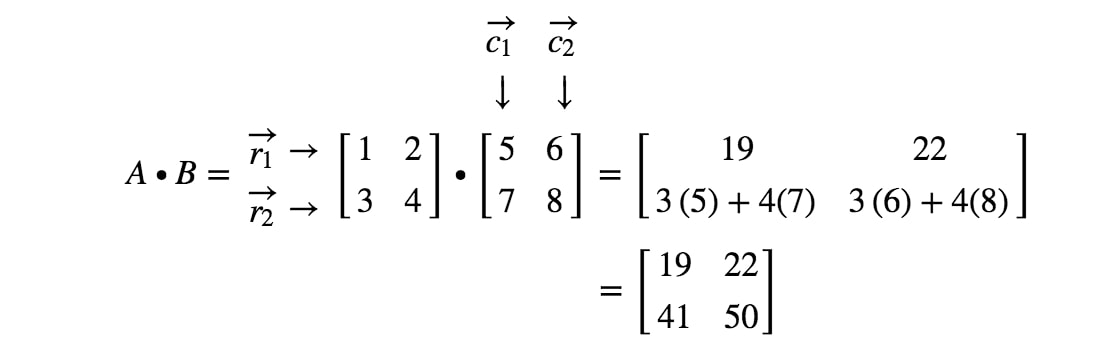
Nu er vi færdige! Dette er, hvad vi får, når vi multiplicerer 2 x 2 matricer. Generelt er matrixmultiplikationsformlen for 2 x 2-matricer

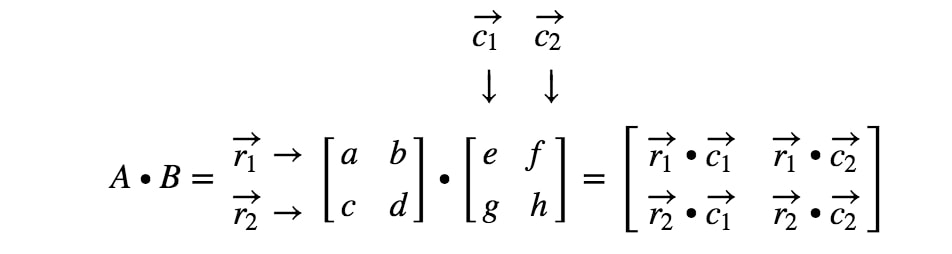
3×3-matrixmultiplikation

Nu ligner processen med en 3 x 3-matrixmultiplikation meget processen med en 2 x 2-matrixmultiplikation. Igen, hvorfor laver vi ikke et eksempel på matrixmultiplikation?

Spørgsmål 4:Find A∙BA \bullet BA∙B if

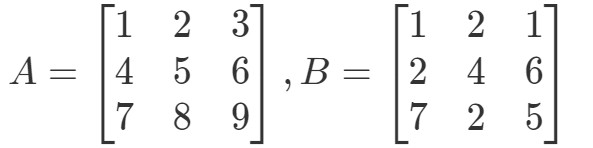
Først skal du bemærke, at multiplikation af dem skulle give os endnu en 3 x 3 matrix. Med andre ord,

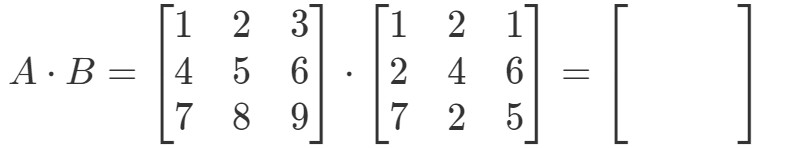
Nu skal vi mærke alle vores rækker i den første matrix og kolonner i den anden matrix.

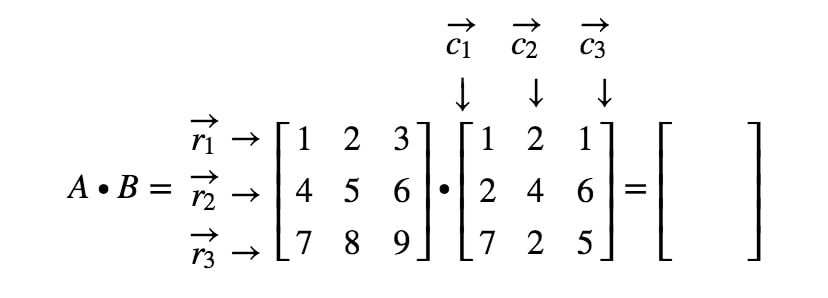
Opmærksomheden henledes på, at den første post i matricen ligger i den 1ste1^{st}1ste række og den 1ste1^{st}1ste kolonne, så vi tager prikproduktet af r1r_{1}r1 og c1c_{1}c1. Dette giver os:

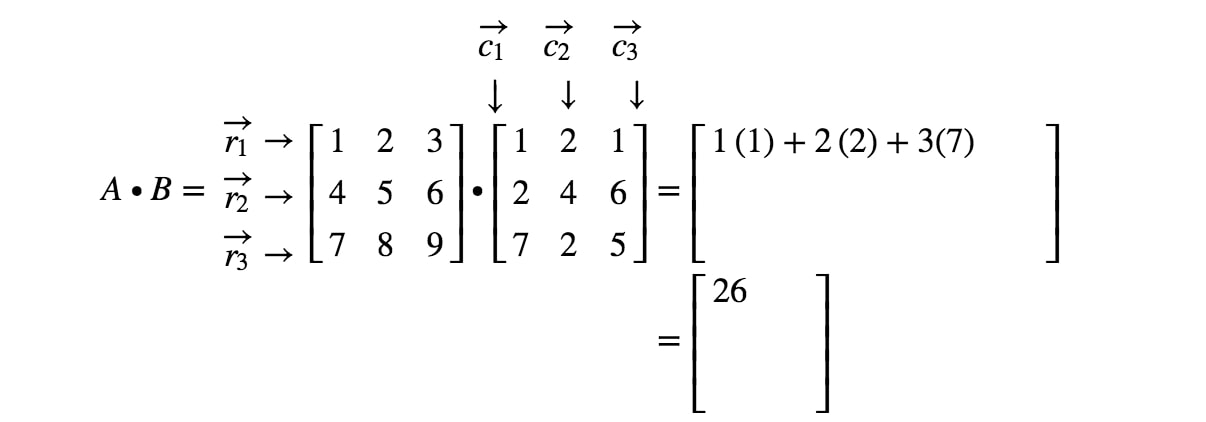
Se nu, at den anden post i matricen er placeret i 1st1^{st}1st række og 2nd2^{{nd}2nd kolonne. Vi tager således prikproduktet af r1r_{1}r1 og c2c_{2}c2. Dette giver os:

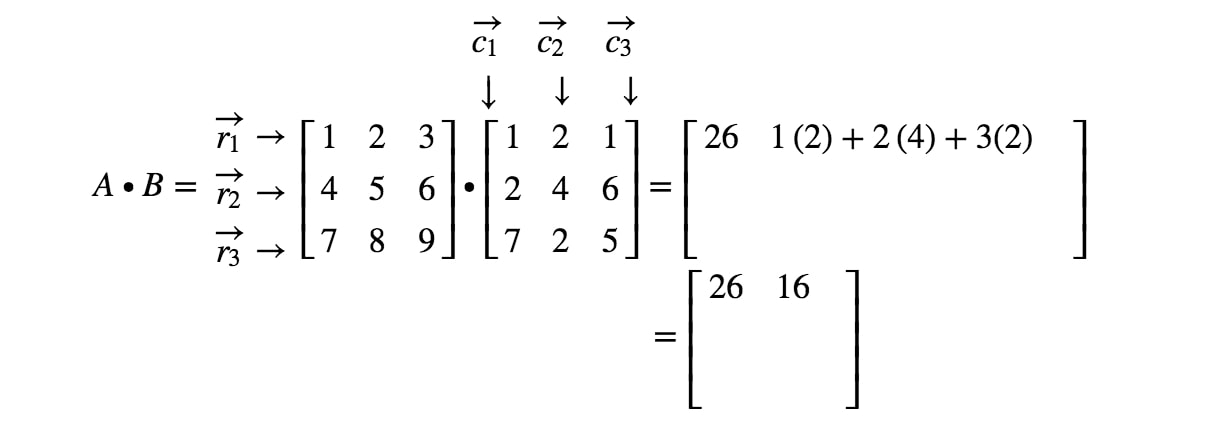
Hvis vi skal blive ved med at finde alle posterne og lave prikproduktet svarende til rækkerne og kolonnerne, så får vi det endelige resultat:

Vi er færdige! Bemærk, at jo større matricerne er, jo mere besværlig bliver matrixmultiplikationen. Det skyldes, at vi skal have med flere og flere tal at gøre! Generelt er matrixmultiplikationsformlen for 3 x 3 matricer

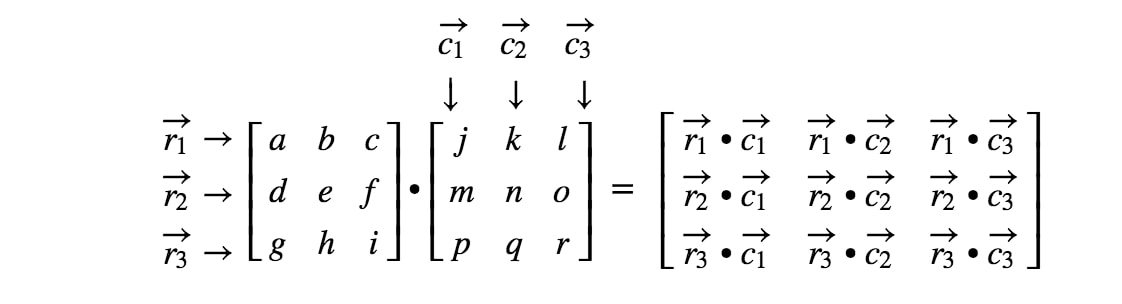
Hvordan multiplicerer man matricer med forskellige dimensioner?

Så vidt vi har multipliceret matricer med samme dimensioner. Desuden ved vi, at multiplikation af to matricer med samme dimension giver en matrix med samme dimensioner. Men hvad sker der, hvis vi multiplicerer en matrix med forskellige dimensioner? Hvordan kan vi kende dimensionerne af den beregnede matrix? Først skal vi se, at multiplikation af matricerne giver en defineret matrix.

Er matricen defineret?

Der er tilfælde, hvor det ikke er muligt at multiplicere to matricer sammen. I disse tilfælde kalder vi matricen for at være udefineret. Hvordan kan vi se, om de er udefinerede?

Produktet af to matricer er kun defineret, hvis antallet af kolonner i den første matrix er lig med antallet af rækker i den anden matrix.

Lad os prøve at bruge denne definition i dette eksempel.

Spørgsmål 5: Lad

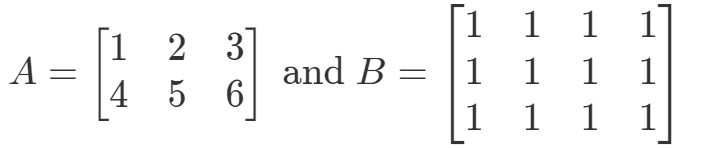
Er A∙BA \bullet BA∙B defineret?

Først skal du bemærke, at den første matrix har 3 kolonner. Også den anden matrix har 3 rækker. Da de begge er lig med 3, så ved jeg, at A∙BA \bullet BA∙B er defineret.

Nu da vi ved, at den er defineret, hvordan vil vi så kende dimensionerne af A∙BA \bullet BA∙B?

Dimensionsevnen

For at finde dimensionerne af A∙BA \bullet BA∙B skal vi først se på dimensionerne af og hver for sig.

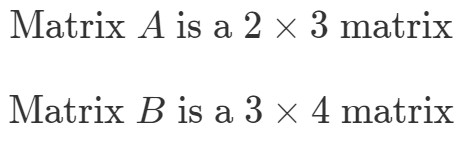
Nu skal vi sætte dimensionerne af matricerne ved siden af hinanden på denne måde:

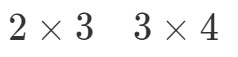
Det vi nu skal gøre er at tage det første tal og det sidste tal og kombinere dem for at få dimensionerne af A∙BA \bullet BA∙B. Se, at det første tal er 2 og det sidste tal er 4. Så dimensionerne af A∙BA \bullet BA∙B bliver:

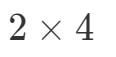
Nu da vi kender dimensionerne af matrixen, kan vi bare beregne hver post ved hjælp af punktprodukterne. Dette vil give os:

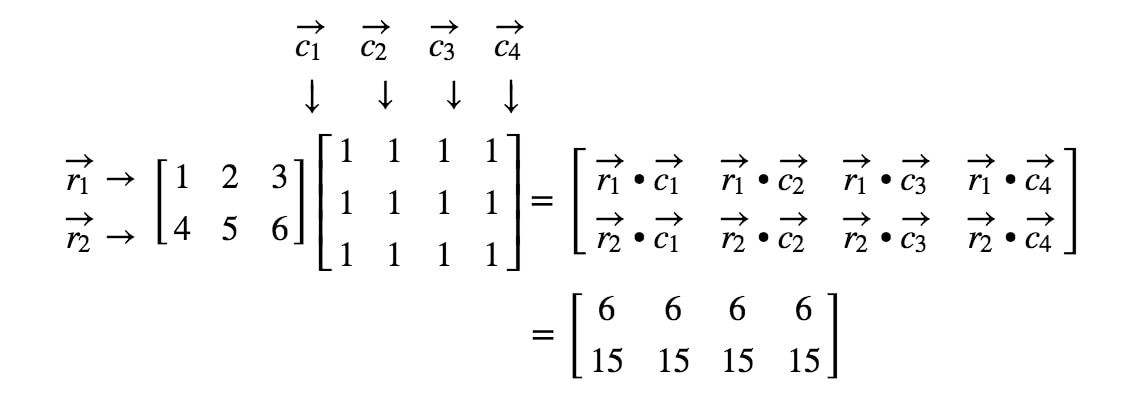
Nu da vi ved, hvordan man multiplicerer matricer meget godt, hvorfor ikke tage et kig på nogle matrixmultiplikationsregler?

Matrixmultiplikationens egenskaber

Så hvilke typer egenskaber har matrixmultiplikation egentlig? Lad os først definere det hele formelt.

Lad X,Y,ZX,ZX, Y, Y, ZX,Y,Z være matricer, InI_{n}In være en identitetsmatrix og OnO_{n}On være en nulmatrix. Hvis alle disse fem matricer har samme dimensioner, vil vi have følgende matrix til matrixmultiplikationsegenskaber:

Den associative egenskab siger, at det er ligegyldigt i hvilken rækkefølge man multiplicerer. Med andre ord, hvis du beregner X∙YX \bullet YX∙Y og derefter multiplicerer med ZZZ, vil du få det samme resultat som at beregne Y∙ZY \bullet ZY∙Z og derefter multiplicere med XXX. Lad os lave et eksempel.

Spørgsmål 6: Vis, at den associative egenskab virker med disse matricer:

Kigger vi på venstre side af ligningen i den associative egenskab, ser vi, at (XY)Z(XY)Z(XY)Z(XY)Z giver:

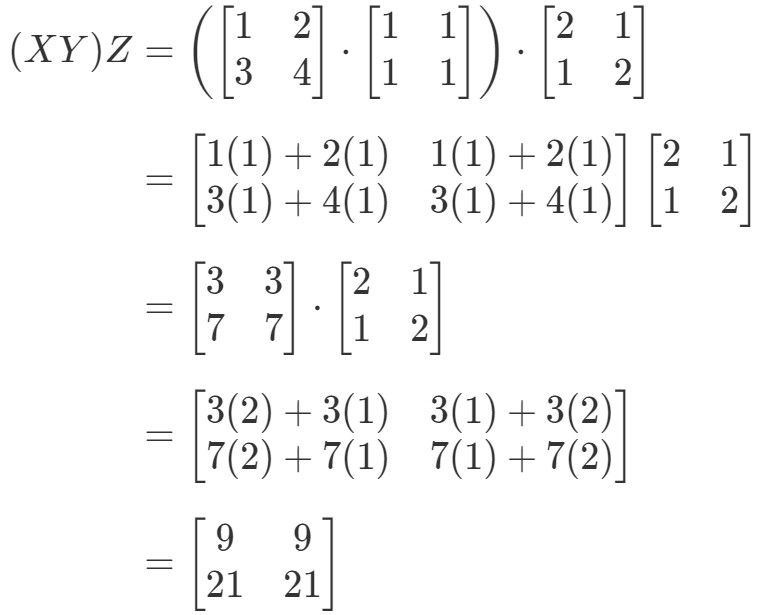
Nu ser vi på ligningens højre side i den associative egenskab og ser, at X(YZ)X(YZ)X(YZ)X(YZ) giver:

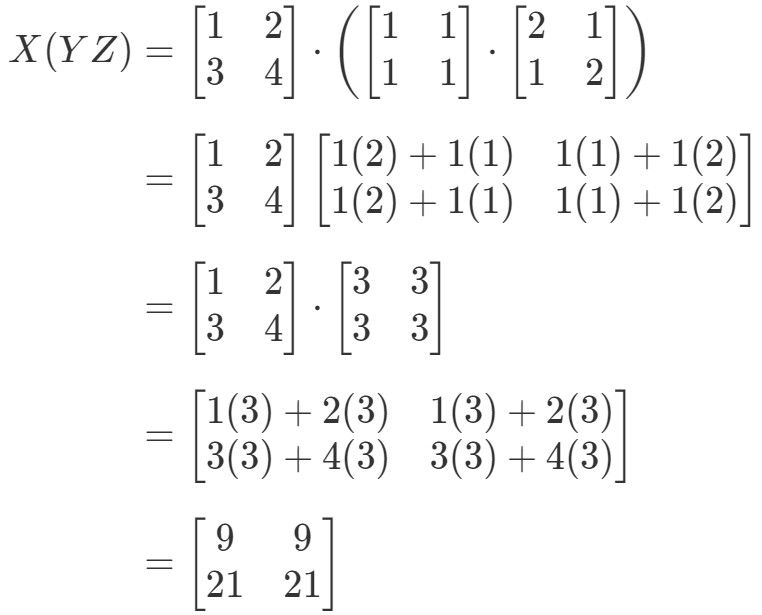
Se, hvordan ligningens venstre side og højre side begge er lige store. Dermed ved vi, at den associative egenskab faktisk virker! Igen betyder det, at matrixmultiplikationsrækkefølgen er ligegyldig!

Nu er den næste egenskab den distributive egenskab. Den distributive egenskab siger, at:

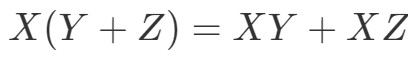
Vi ser, at vi også har lov til at bruge folieteknikken til matricer. Bare for at vise, at denne egenskab virker, skal vi lave et eksempel.

Spørgsmål 7: Vis, at den distributive egenskab virker for følgende matricer:

Se, at venstre side af ligningen er X(Y+Z)X(Y + Z)X(Y + Z)X(Y+Z). Derfor giver beregning af det os:

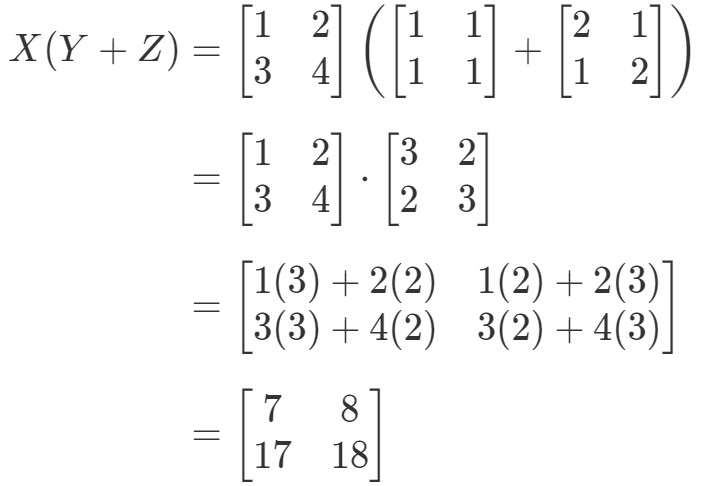
Nu skal vi undersøge, om ligningens højre side giver os præcis det samme. Bemærk, at ligningens højre side er XY+XZXY+XZXY + XZXY+XZ. Hvis vi beregner dette, får vi:

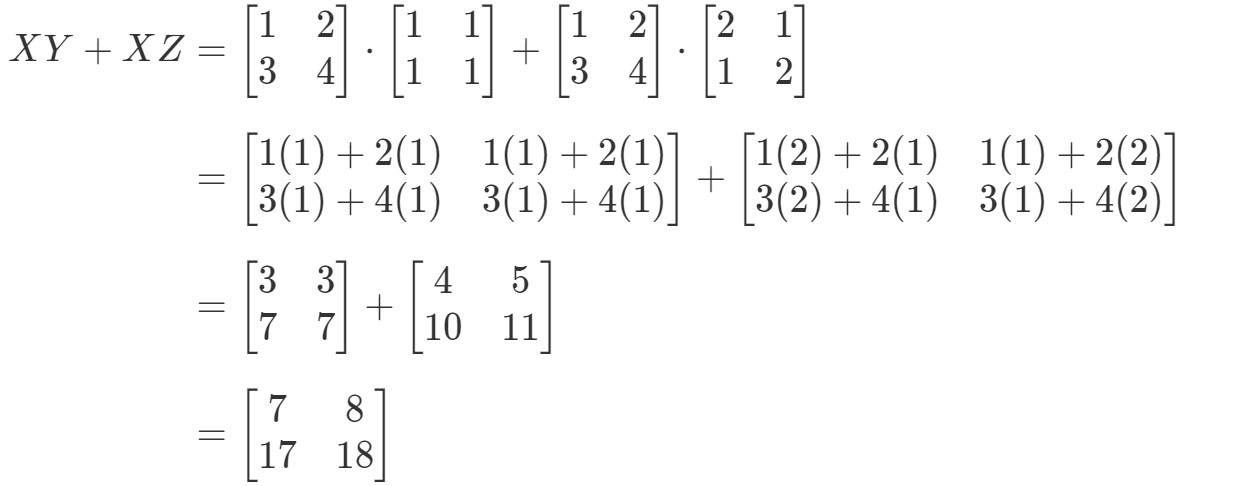
Bemærk, at ligningens venstre side er nøjagtig den samme som ligningens højre side. Derfor kan vi bekræfte, at den distributive egenskab faktisk virker.

Er matrixmultiplikation kommutativ?

Vi ved, at matrixmultiplikation opfylder både den associative og distributive egenskab, men vi har slet ikke talt om den kommutative egenskab. Betyder det, at matrixmultiplikation ikke opfylder den? Det gør den faktisk ikke, og vi kan kontrollere det med et eksempel.

Spørgsmål 8: Hvis matrixmultiplikation er kommutativ, så må følgende være sandt:

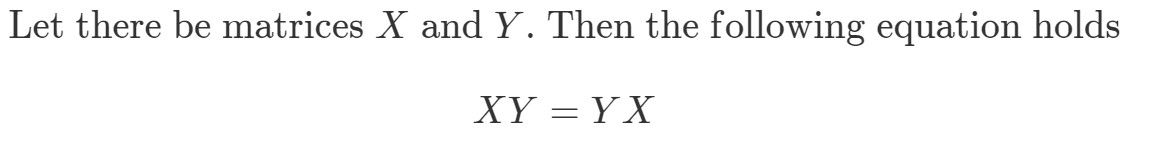
Vis, at XYeqYXXY eq YXXYeqYX hvis

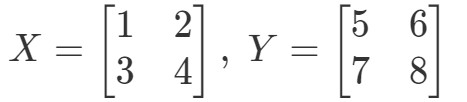
Først beregner vi venstre side af ligningen. Ved at beregne XYXYXYXY får vi:

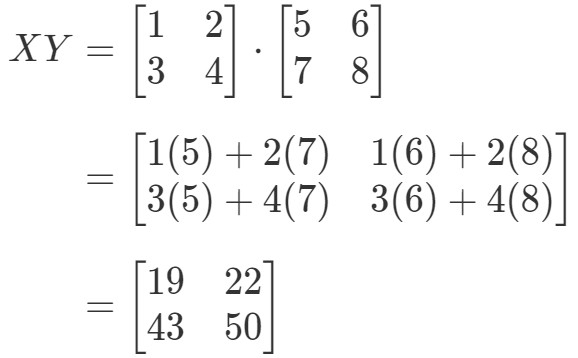
Nu beregner vi ligningens højre side, og får:

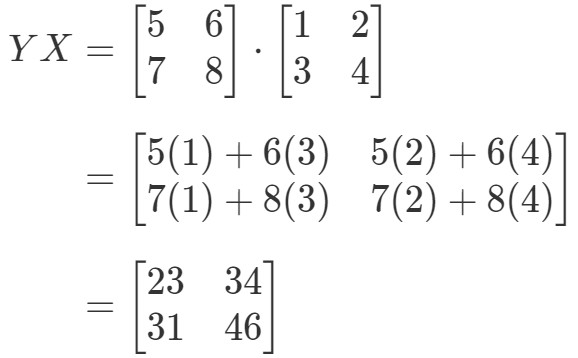
Som du kan se,

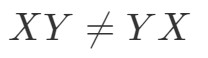
For vi har

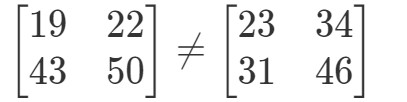
Disse to matricer er helt forskellige.

Nu er der stadig et par egenskaber mere ved multiplikation af matricer. Disse egenskaber omhandler dog nul- og identitetsmatricer.

Matrixmultiplikation for nulmatrixen

Matrixmultiplikationsegenskaben for nulmatrixen siger følgende:

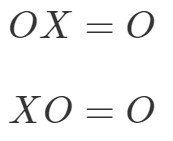
hvor OOO er en nulmatrix.

Det betyder, at hvis du multiplicerer en nulmatrix med en anden matrix, der ikke er nul, vil du få en nulmatrix. Lad os teste om dette er sandt med et eksempel.

Spørgsmål 9: Vis at ligningen OX=OOX = OOX=O og XO=OXO = OXO=O gælder hvis:

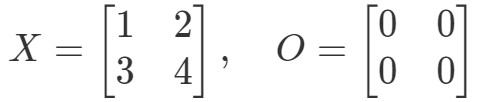
Lad os først se på ligningen

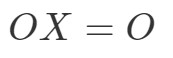
Bemærk, at beregning af OXOXOXOX giver os:

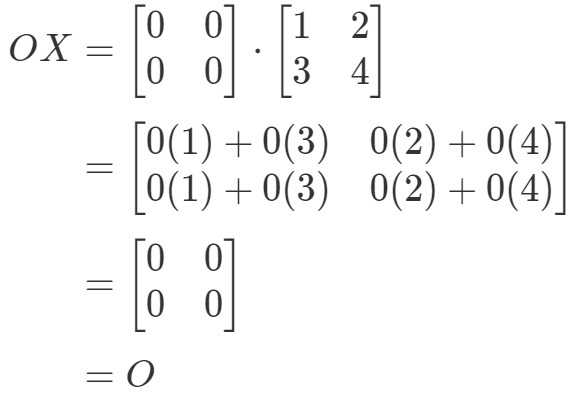
Vi ser, at OX=OOX = OOX=O, så ligningen holder. Tilsvarende, hvis vi beregner XOXOXOXO, får vi:

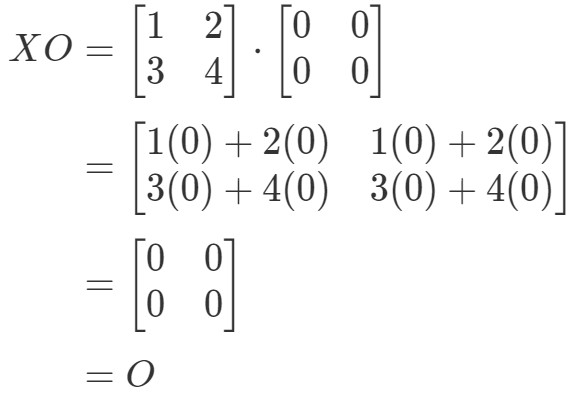
Vi kan se, at ligningen XO=OXO = OXO=O holder, så vi er færdige.

Matrixmultiplikation for identitetsmatricen

Hvad med matrixmultiplikationsegenskaben for identitetsmatricer? Jo, egenskaben siger følgende:

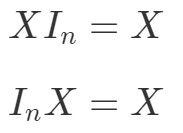
hvor InI_{n}In er en n×nn \ gange nn×n identitetsmatrix. Igen kan vi se, at følgende ligninger holder med et eksempel.

Spørgsmål 10: Vis, at ligningerne XI2=XX I_{2} = XXI2=X og I2X=XI_{2} X = XI2X=X gælder med følgende matricer

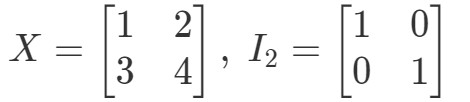
Så for ligningen XI2=XX I_{2} = XXI2=X har vi:

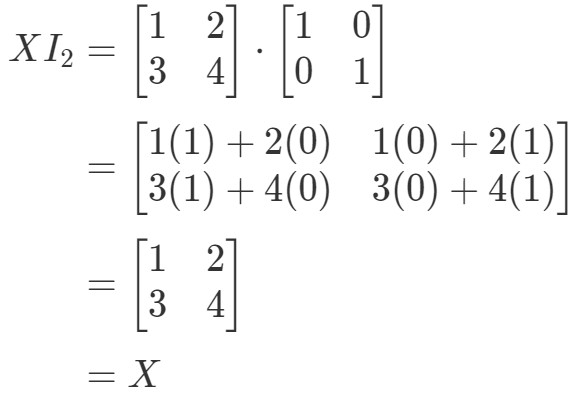
Så ligningen holder altså. I lighed med ligningen I2X=XI_{2}X = XI2X=X har vi:

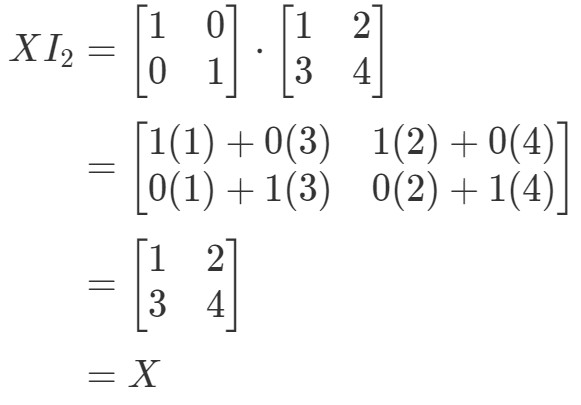
Igen holder ligningen. Så vi er færdige med spørgsmålet, og begge ligninger holder, hvilket afslutter alle egenskaberne ved matrixmultiplikation. Hvis du nu vil se på en konkret anvendelse af matrixmultiplikation, så vil jeg anbefale dig at kigge på denne artikel.

https://www.mathsisfun.com/algebra/matrix-multiplying.html