Free Press

Mátrix szorzás

A mátrixok szorzásának pontosan két módja van. Az első mód a mátrix skalárral való szorzása. Ezt skaláris szorzásnak nevezzük. A második mód egy mátrix szorzása egy másik mátrixszal. Ezt nevezzük mátrixszorzásnak.

Skalárszorzás

A szkalárszorzás valójában egy nagyon egyszerű mátrixművelet. Ahhoz, hogy egy skalárt megszorozzunk egy mátrixszal, egyszerűen fogjuk a skalárt, és megszorozzuk a mátrix minden egyes bejegyzésével. Nézzünk egy példát.

Kérdés 1: Számítsuk ki a 2A2A2A ha

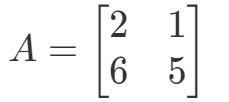
A kérdés azt kéri, hogy találjuk ki, mi a 2A2A2A2A. Más szóval, azt keressük, hogy

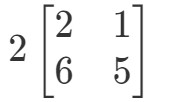
Megjegyezzük, hogy ha a mátrix minden egyes bejegyzéséhez 2-t szorzunk, akkor azt kapjuk, hogy:

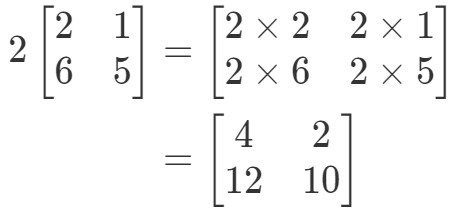
Nagyon egyszerű! Csináljunk egy másikat.

Kérdés 2: Számítsuk ki a 0A0A0A ha

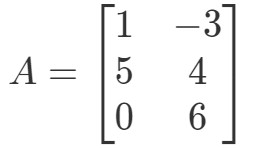
Még egyszer megpróbáljuk megtalálni a 0A0A0A-t. Ez azt jelenti, hogy a

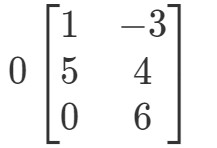
A mátrix furcsa alakú lesz, de a koncepció ugyanaz marad. Továbbra is a 0 skalárt fogjuk a mátrix minden egyes bejegyzéséhez szorozni. Ha így teszünk, akkor:

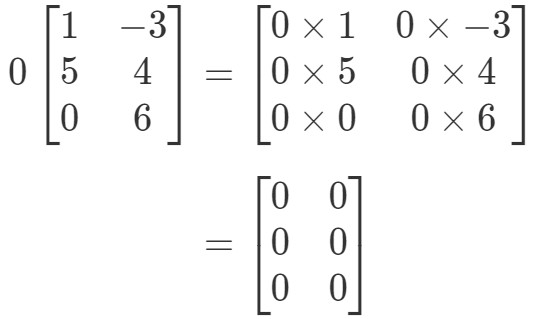
Vegyük észre, hogy a mátrix minden bejegyzése 0. Ez az úgynevezett nullmátrix, amely 3 x 2.

Most, hogy már nagyon jól ismerjük a skaláris szorzást, miért nem térünk át a mátrixszorzásra?

Hogyan szorozzuk a mátrixokat

Hogyan szorozzunk egy mátrixot egy másik mátrixszal, először meg kell tanulnunk, mi az a pontszorzat.

Mi az a pontszorzat?

A pontszorzat (más néven vektorszorzás) két vektor szorzatának kiszámítási módja. Legyen például a két vektor:

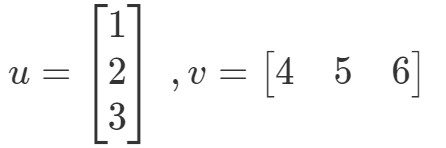
Hogyan szoroznám meg ezt a két vektort? Egyszerűen csak szorozzuk meg a megfelelő tételeket, és adjuk össze a szorzatokat. Más szóval,

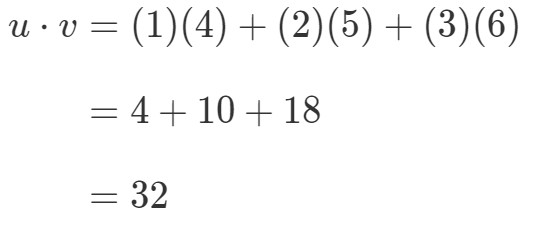
A vektorok szorzásából tehát egyetlen értéket kapunk. Figyeljük meg azonban, hogy a két vektornak azonos számú bejegyzése van. mi van akkor, ha az egyik vektornak más számú bejegyzése van, mint a másiknak? Legyen például

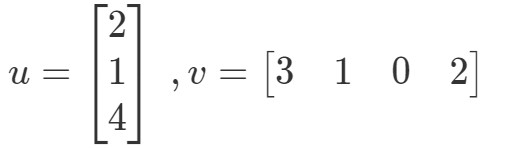
Ha a megfelelő bejegyzéseket megszoroznám és összeadnám, akkor azt kapnám:

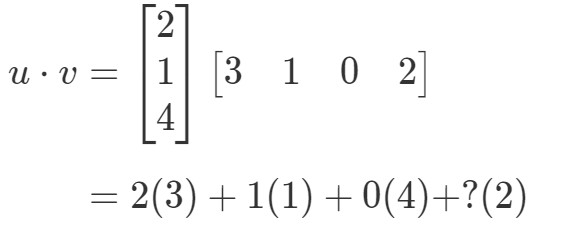
Itt van egy probléma. Az első három bejegyzésnek vannak megfelelő bejegyzései, amelyekkel szorozni lehet, de az utolsó bejegyzésnek nincsenek. Mit tegyünk tehát itt? A válasz az, hogy itt nem tehetünk semmit. Ez csak azt jelenti, hogy nem tudjuk kiszámítani ennek a két vektornak a pontszorzatát.

Végeredményben tehát nem tudjuk megtalálni két olyan vektor pontszorzatát, amelyeknek különböző számú bejegyzése van. Ugyanannyi bejegyzéssel kell rendelkezniük.

2 x 2 mátrixszorzás

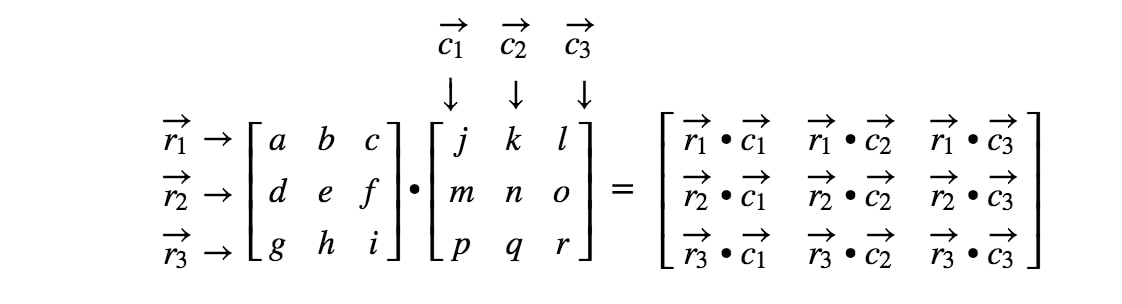
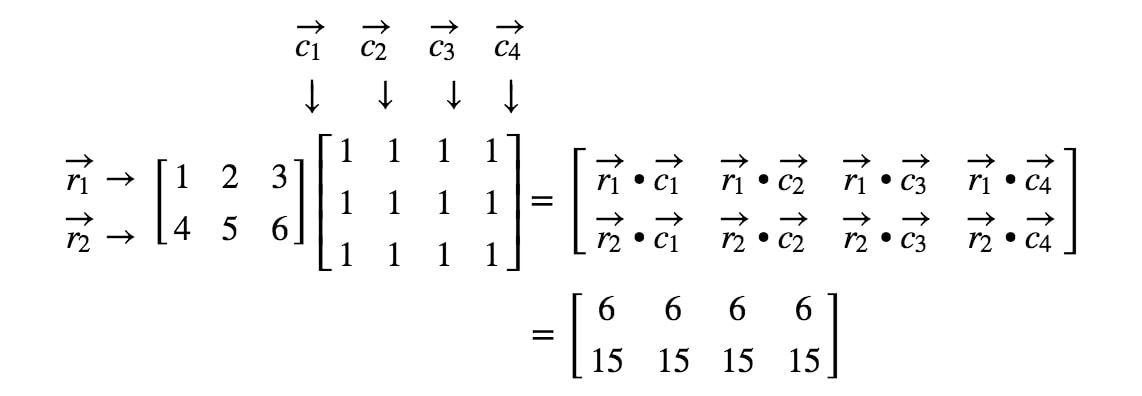
Szóval mi értelme volt megtanulni a pontszorzatot? Nos, a pontszorzatot akkor fogjuk használni, amikor két mátrixot szorzunk össze. Amikor egy mátrixot szorzunk egy másik mátrixszal, a sorokat és oszlopokat vektorként akarjuk kezelni. Pontosabban, az első mátrix minden sorát vektorként, a második mátrix minden oszlopát pedig vektorként akarjuk kezelni. Nézzünk egy példát.

Kérdés 3: Keressük meg A∙BA \bullet BA∙B ha

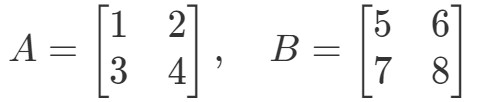
A két mátrix szorzásával megkapjuk:

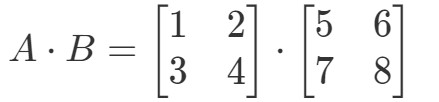
Most a sorok és az oszlopok, amelyekre fókuszálunk

ahol r1r_{1}r1 az első sor, r2r_{2}r2 a második sor, és, c1,c2c_{1}, c_{2}c1,c2 az első és második oszlop. Most minden egyes sort és oszlopot, amit itt látunk, vektorként fogunk kezelni.

Megjegyezzük itt, hogy egy 2 x 2 mátrixot megszorozva egy másik 2 x 2 mátrixszal egy 2 x 2 mátrixot kapunk. Más szóval, a kapott mátrixnak 4 bejegyzéssel kell rendelkeznie.

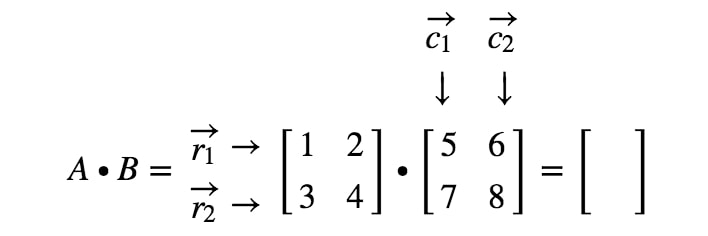
Hogyan kapjuk pontosan az első bejegyzést? Nos, vegyük észre, hogy az első bejegyzés az első sorban és az első oszlopban található. Tehát egyszerűen vesszük az r1r_{1}r1 és a c1c_{1}c1 pontszorzatát. Így az első bejegyzés a következő lesz

Hogyan kapjuk meg ezúttal a második bejegyzést? Nos, figyeljük meg, hogy a második bejegyzés helye az első sorban és a második oszlopban van. Tehát egyszerűen vesszük az r1r_{1}r1 és a c2c_{2}c2 pontszorzatát. Így a második bejegyzés a következő lesz

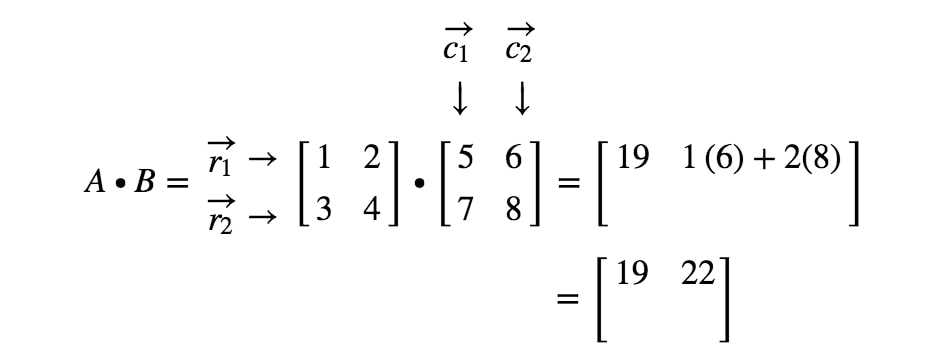
Most ugyanezt a stratégiát fogjuk használni az utolsó két bejegyzés keresésére. Vegyük észre, hogy az utolsó előtti bejegyzés a 2nd2^{nd}2. sorban és az 1st1^{st}1. oszlopban található, az utolsó bejegyzés pedig a 2nd2^{nd}2. sorban és a 2nd2^{nd}2. oszlopban. Tehát vesszük az r2r_{2}r2 és a c1c_{1}c1, valamint az r2r_{2}r2 és a c2c_{2}c2 pontproduktumát. Így megkapjuk:

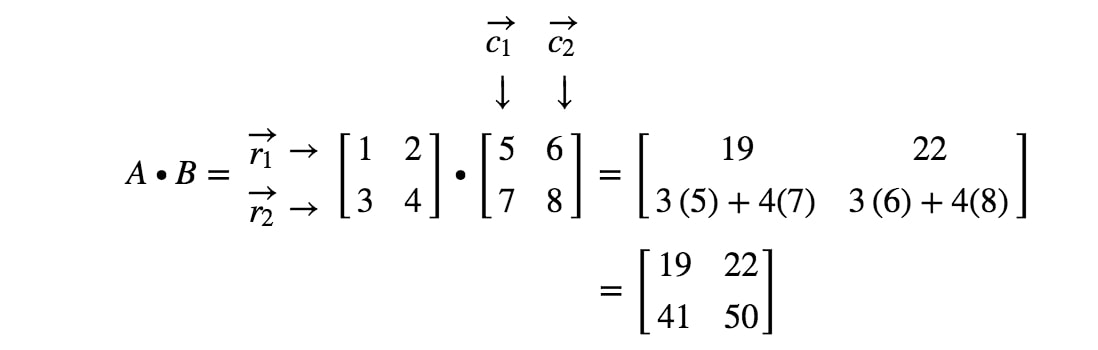
Most már készen vagyunk! Ezt kapjuk, ha 2 x 2 mátrixot szorzunk. Általában a 2 x 2 mátrixok mátrixszorzási képlete a következő

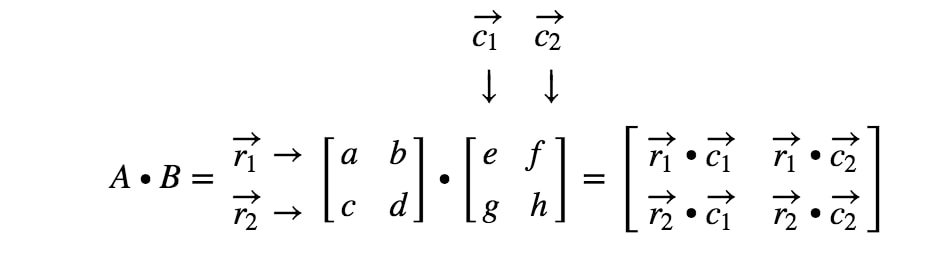
3×3 mátrixszorzás

Most a 3 x 3 mátrixszorzás folyamata nagyon hasonló a 2 x 2 mátrixszorzás folyamatához. Ismételjük meg, miért nem csinálunk egy mátrixszorzási példát?

Kérdés 4:Keressük meg A∙BA \bullet BA∙B ha

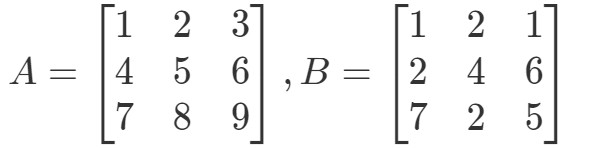
Először is, vegyük észre, hogy a szorzással egy másik 3 x 3 mátrixot kell kapnunk. Más szóval,

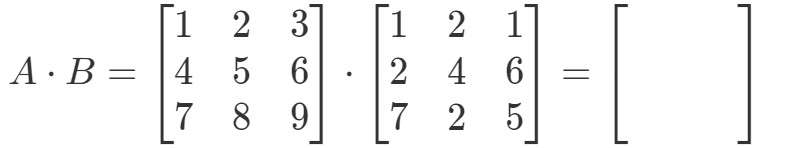
Most címkézzük fel az első mátrix összes sorát és a második mátrix oszlopait.

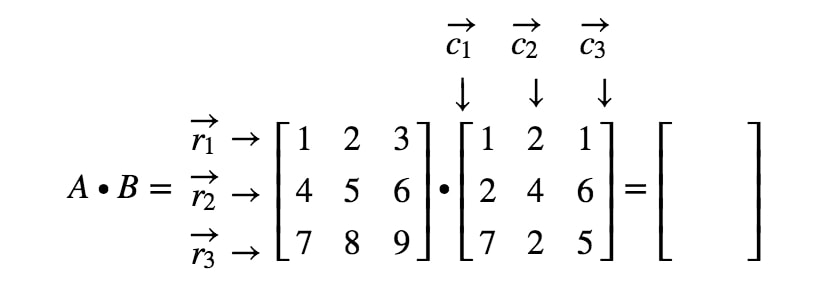
Megjegyezzük, hogy a mátrix első bejegyzése az 11^{st}1. sorban és az 1^{st}1. oszlopban található, ezért az r1r_{1}r1 és c1c_{1}c1 pontproduktumát vesszük. Így megkapjuk:

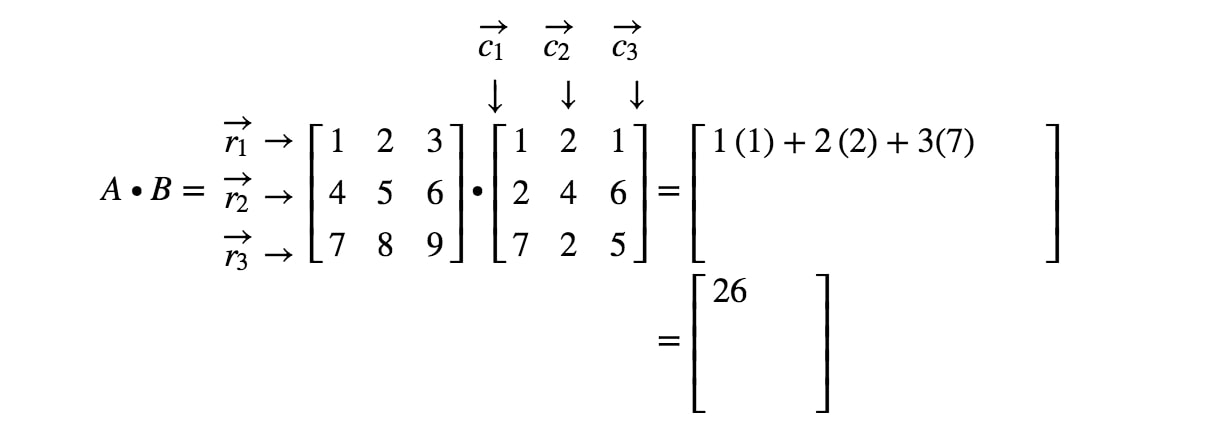
Most figyeljük meg, hogy a mátrix második bejegyzése az 1.1^{st}1. sorban és a 2.2^{nd}2. oszlopban található. Így az r1r_{1}r1 és a c2c_{2}c2 pontszorzatát vesszük. Így megkapjuk:

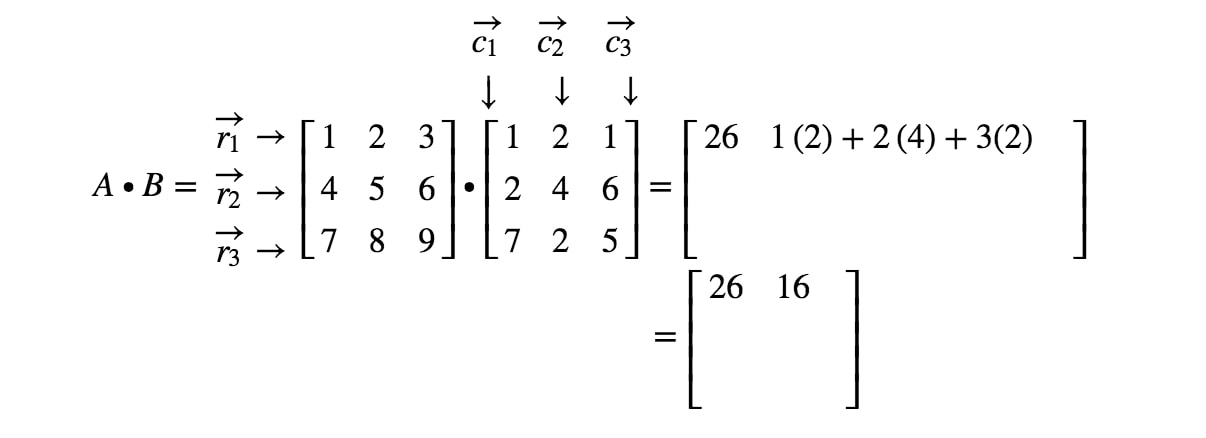
Ha továbbra is megkeressük az összes bejegyzést, és elvégezzük a soroknak és oszlopoknak megfelelő pontszorzatot, akkor megkapjuk a végeredményt:

Készen vagyunk! Vegyük észre, hogy minél nagyobbak a mátrixok, annál fáradságosabb lesz a mátrixszorzás. Ennek az az oka, hogy egyre több számmal kell foglalkoznunk! Általánosságban a 3 x 3 mátrixok mátrixszorzási képlete a következő:

Hogyan szorozzuk a különböző méretű mátrixokat?

Eleddig azonos méretű mátrixokat szoroztunk. Továbbá tudjuk, hogy két azonos dimenziójú mátrix szorzása azonos dimenziójú mátrixot ad. De mi történik, ha különböző dimenziójú mátrixokat szorzunk? Honnan tudnánk a kiszámított mátrix dimenzióit? Először is meg kell néznünk, hogy a mátrixok szorzása definiált mátrixot ad-e.

A mátrix definiált?

Vannak olyan esetek, amikor nem lehet két mátrixot összeszorozni. Ezekben az esetekben a mátrixot definiálatlannak nevezzük. Honnan tudjuk, hogy nem definiáltak?

Két mátrix szorzata csak akkor definiált, ha az első mátrix oszlopainak száma megegyezik a második mátrix sorainak számával.

Próbáljuk meg ezt a definíciót ebben a példában alkalmazni.

Kérdés 5: Legyen

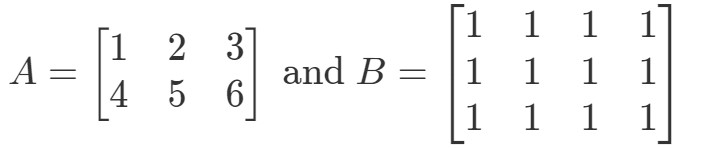
A∙BA \bullet BA∙B definiált?

Először is vegyük észre, hogy az első mátrixnak 3 oszlopa van. A második mátrixnak is 3 sora van. Mivel mindkettő egyenlő 3-mal, akkor tudom, hogy A∙BA \bullet BA∙B definiált.

Most, hogy tudjuk, hogy definiált, honnan tudnánk meg A∙BA \bullet BA∙B méreteit?

A dimenziós tulajdonság

Hogy megtaláljuk A∙BA \bullet BA∙B dimenzióit, először külön-külön meg kell vizsgálnunk a és dimenzióit.

Most így fogjuk egymás mellé tenni a mátrixok dimenzióit:

Azt fogjuk most tenni, hogy fogjuk az első és az utolsó számot, és kombinálva megkapjuk A∙BA \bullet BA∙B dimenzióit. Látjuk, hogy az első szám 2, az utolsó szám pedig 4. Tehát az A∙BA \bullet BA∙B dimenziói a következők lesznek:

Most, hogy tudjuk a mátrix dimenzióit, egyszerűen kiszámíthatjuk az egyes bejegyzéseket a pontproduktumok segítségével. Így megkapjuk:

Most, hogy már nagyon jól tudjuk, hogyan kell mátrixokat szorozni, miért nem nézünk meg néhány mátrixszorzási szabályt?

Mátrixszorzás tulajdonságai

Hát milyen tulajdonságai vannak valójában a mátrixszorzásnak? Először is definiáljunk mindent formálisan.

Legyen X,Y,ZX, Y, ZX,Y,Z mátrix, InI_{n}In egy azonossági mátrix, OnO_{n}On pedig egy nullmátrix. Ha mind az öt mátrix egyenlő dimenziójú, akkor a következő mátrix-mátrix szorzási tulajdonságokkal rendelkezünk:

Az asszociatív tulajdonság azt mondja ki, hogy nem számít, milyen sorrendben szorzunk. Más szóval, ha kiszámítjuk X∙YX \bullet YX∙Y-t, majd megszorozzuk ZZZ-el, ugyanazt az eredményt kapjuk, mintha kiszámítjuk Y∙ZY \bullet ZY∙Z-t, majd megszorozzuk XXX-el. Nézzünk egy példát.

6. kérdés: Mutassuk meg, hogy az asszociatív tulajdonság működik ezekkel a mátrixokkal:

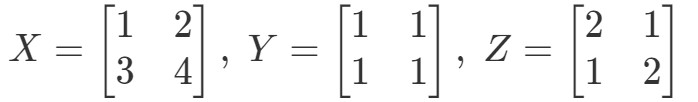
Az egyenlet bal oldalát vizsgálva az asszociatív tulajdonságban azt látjuk, hogy (XY)Z(XY)Z(XY)Z(XY)Z adja:

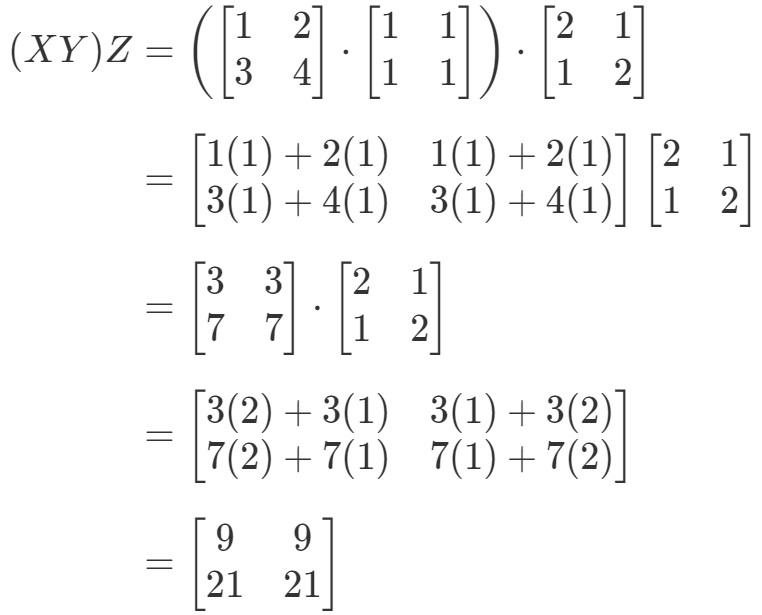
Most az egyenlet jobb oldalát vizsgálva az asszociatív tulajdonságban azt látjuk, hogy X(YZ)X(YZ)X(YZ) adja:

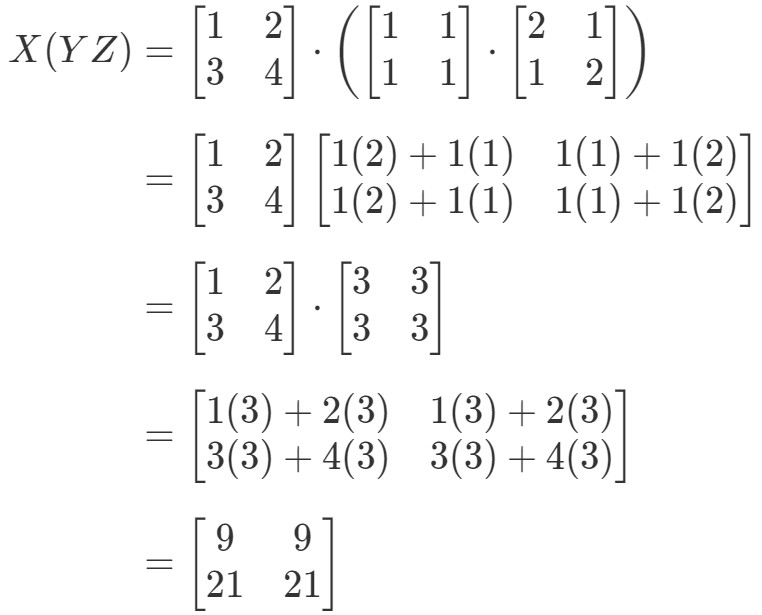
Nézzük, hogy az egyenlet bal és jobb oldala is egyenlő. Ebből tudjuk, hogy az asszociatív tulajdonság valóban működik! Ez ismét azt jelenti, hogy a mátrix szorzási sorrendje nem számít!

A következő tulajdonság a disztributív tulajdonság. A disztributív tulajdonság kimondja, hogy:

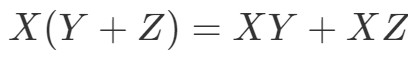
Láthatjuk, hogy a fóliatechnikát használhatjuk a mátrixok esetében is. Csak hogy megmutassuk, hogy ez a tulajdonság működik, csináljunk egy példát:

Kérdés 7: Mutassuk meg, hogy a disztributív tulajdonság működik a következő mátrixokra:

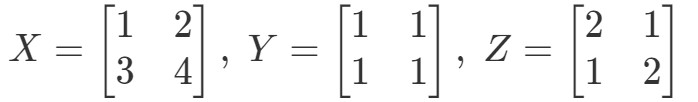
Lássuk, hogy az egyenlet bal oldala X(Y+Z)X(Y + Z)X(Y+Z). Ezért ennek kiszámításával megkapjuk:

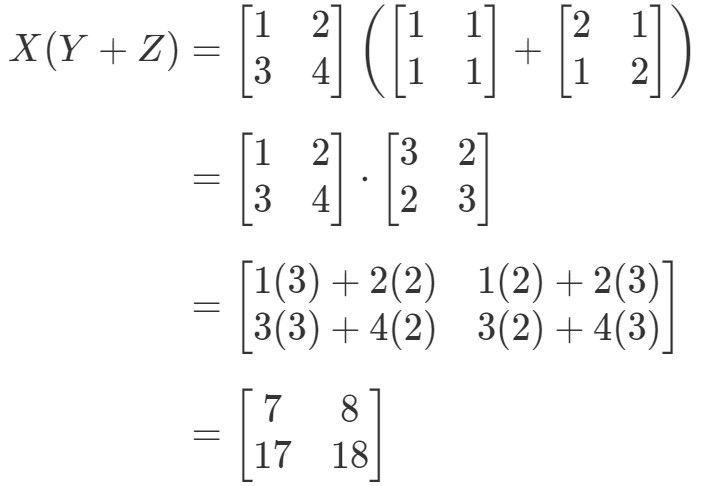
Most nézzük meg, hogy az egyenlet jobb oldala pontosan ugyanazt adja-e nekünk. Vegyük észre, hogy az egyenlet jobb oldala XY+XZXY + XZXY+XZ. Ennek kiszámításával megkapjuk:

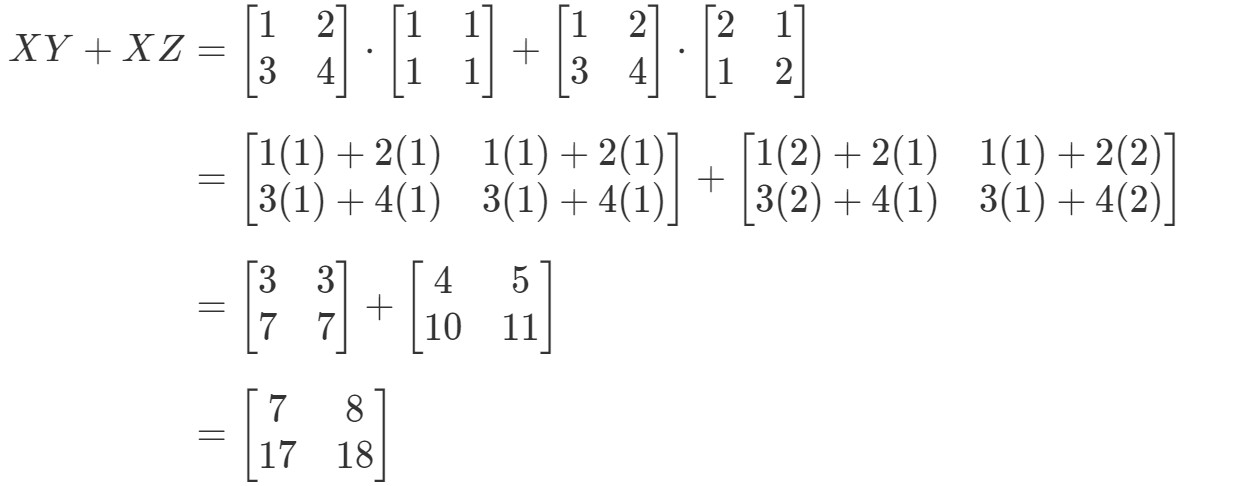
Megjegyezzük, hogy az egyenlet bal oldala pontosan ugyanaz, mint az egyenlet jobb oldala. Így megerősíthetjük, hogy a disztributív tulajdonság valóban működik.

A mátrixszorzás kommutatív?

Tudjuk, hogy a mátrixszorzás mind az asszociatív, mind a disztributív tulajdonságnak megfelel, azonban a kommutatív tulajdonságról egyáltalán nem beszéltünk. Ez azt jelenti, hogy a mátrixszorzás nem felel meg ennek? Valójában nem, és ezt egy példával ellenőrizhetjük is.

8. kérdés: Ha a mátrixszorzás kommutatív, akkor a következőnek igaznak kell lennie:

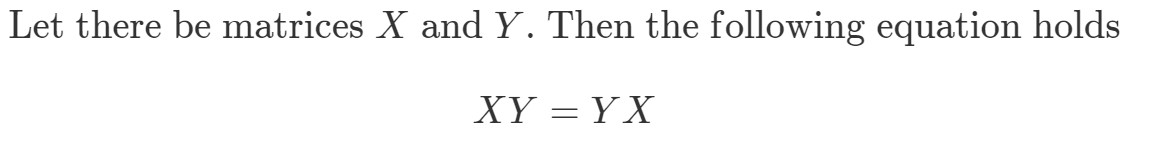
Mutassuk meg, hogy XYeqYXXY eq YXXYeqYX ha

Először is kiszámítjuk az egyenlet bal oldalát. XYXYXY kiszámításával megkapjuk:

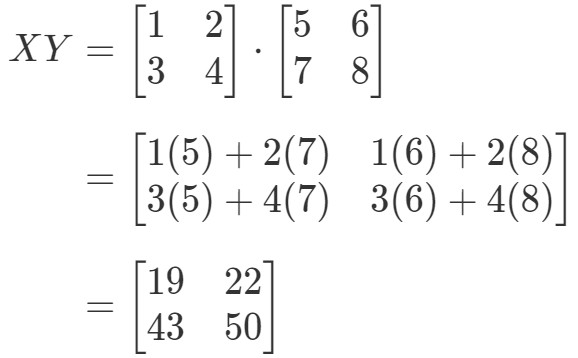
Most az egyenlet jobb oldalát kiszámítva megkapjuk:

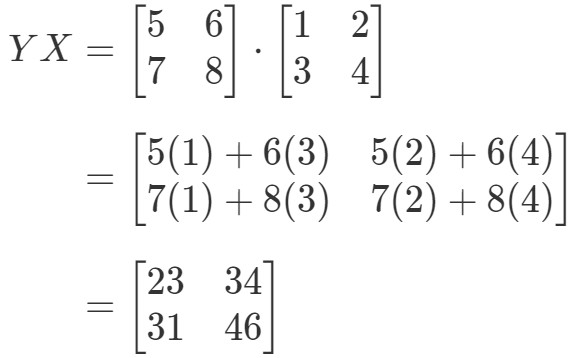
Mint látható,

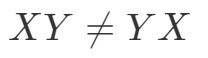
Mert van

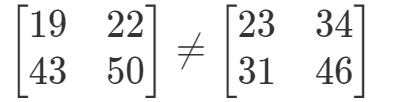
Ez a két mátrix teljesen más.

Most van még néhány tulajdonsága a mátrixok szorzatának. Ezek a tulajdonságok azonban a nullmátrixokkal és az azonossági mátrixokkal foglalkoznak.

Mátrixszorzás a nullmátrixra

A nullmátrixra vonatkozó mátrixszorzási tulajdonság a következőket mondja ki:

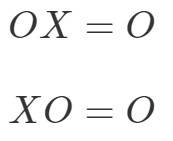
amelyben OOO egy nullmátrix.

Ez azt jelenti, hogy ha egy nullás mátrixot megszorozunk egy másik nem nullás mátrixszal, akkor egy nullás mátrixot kapunk. Próbáljuk ki egy példával, hogy ez igaz-e.

Kérdés 9: Mutassuk meg, hogy az OX=OOX = OOX=O és XO=OXO = OXO=O egyenlet akkor érvényes, ha:

Nézzük először az egyenletet

Megjegyezzük, hogy OXOXOX kiszámításával megkapjuk:

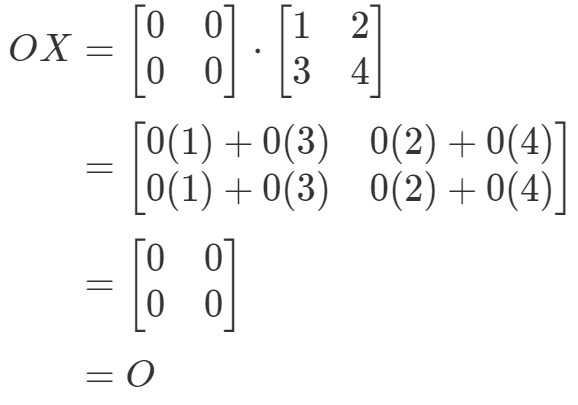
Látjuk, hogy OX=OOX = OOX=O, tehát az egyenlet érvényes. Hasonlóképpen, ha kiszámítjuk XOXOXO-t, akkor azt kapjuk:

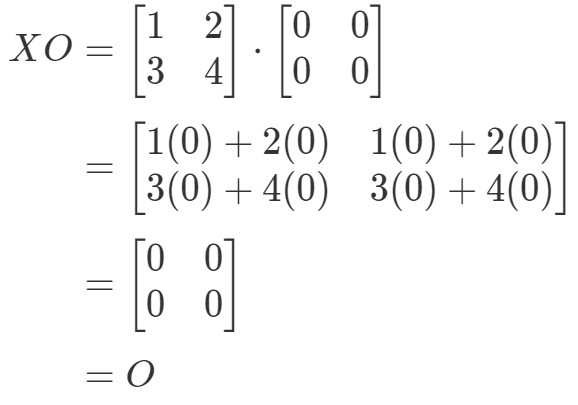
Azt látjuk, hogy az XO=OXO = OXO=O egyenlet érvényes, tehát készen vagyunk.

Mátrixszorzás az azonossági mátrixra

Most mi a helyzet az azonossági mátrixok mátrixszorzási tulajdonságával? Nos, a tulajdonság a következőket mondja ki:

ahol InI_{n}In egy n×nn \times nn×n azonossági mátrix. Ismét egy példán keresztül láthatjuk, hogy a következő egyenletek valóban érvényesek.

Kérdés 10: Mutassuk meg, hogy a XI2=XX I_{2} = XXI2=X és az I2X=XI_{2} X = XI2X=X érvényesek a következő mátrixokkal

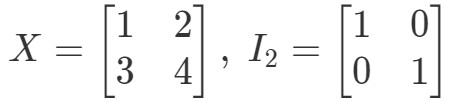
Az XI2=XX I_{2} = XXI2=X egyenletre tehát:

Az egyenlet tehát valóban érvényes. Az I2X=XI_{2}X = XI2X=X egyenlethez hasonlóan:

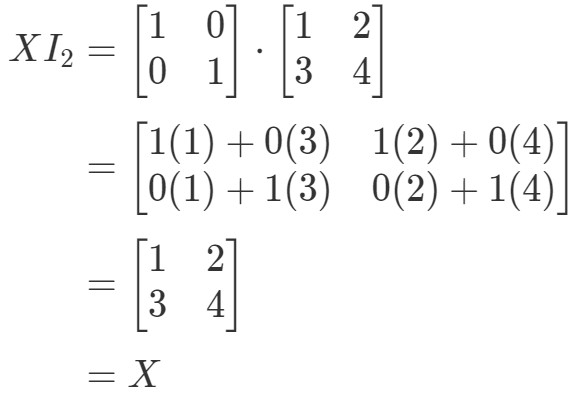
Ismét érvényes az egyenlet. Tehát végeztünk a kérdéssel, és mindkét egyenlet érvényes, ezzel lezártuk a mátrixszorzás összes tulajdonságát. Ha most a mátrixszorzás egy valós életbeli alkalmazását szeretnéd megnézni, akkor ajánlom, hogy nézd meg ezt a cikket.

https://www.mathsisfun.com/algebra/matrix-multiplying.html