行列の掛け算
行列の掛け算にはちょうど2つの方法があります。 最初の方法は行列とスカラーを掛けることです。 これはスカラー倍算として知られています。 2つ目の方法は、行列と別の行列を掛けることです。 3274>
Scalar Multiplication
scalar multiplicationは、実際には非常に単純な行列演算です。 スカラーと行列を掛けるには、単にスカラーをとって行列の各エントリに掛けるだけです。
Question 1: Calculate 2A2A2A if
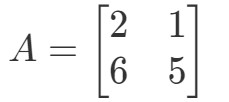
この問題は、2A2A2Aが何かを求めているのですね。 つまり、
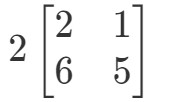
行列の各エントリに2を掛けると、次のようになることに注意してください:
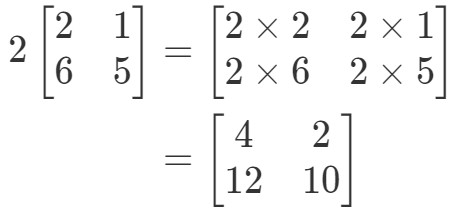
非常に簡単ですね。 もう一つやってみましょう。
問題2:0A0A0Aを計算する場合
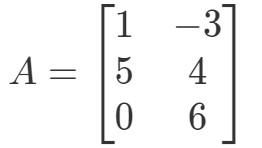
ここでも0A0A0Aを求めています。 つまり、
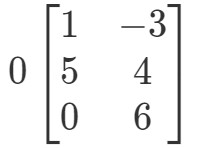
行列は奇妙な形になりますが、考え方は同じです。 行列の各エントリにスカラー0を乗じることに変わりはありません。 そうすると、
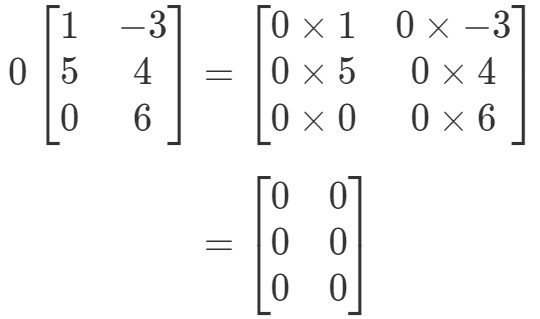
この行列のエントリはすべて0であることに注意してください。これは、3×2のゼロ行列として知られています。
行列の乗算方法
行列と別の行列を乗算するには、まず、ドットプロダクトとは何かについて学習する必要があります。 例えば、2つのベクトルを
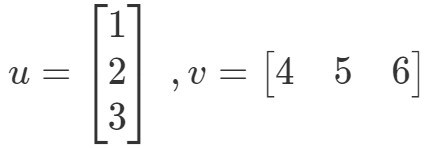
この2つのベクトルはどのように掛けるのでしょう。 単純に、対応する項目を掛け合わせ、その積を足せばよいのです。 つまり、
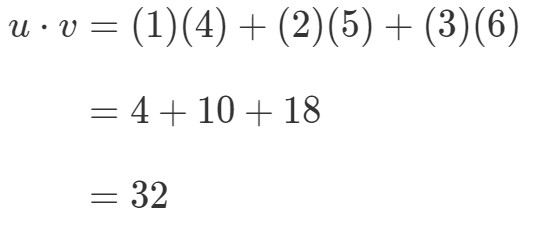
このように、ベクトルを掛けると一つの値になるのですね。 しかし、2つのベクトルが同じ数の項目を持つことに注目してください。一方のベクトルが他方のベクトルと異なる数の項目を持つ場合はどうでしょうか。 例えば、
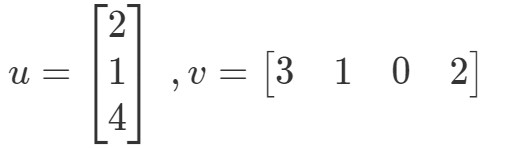
対応する項目を掛け合わせて、全部足すと、
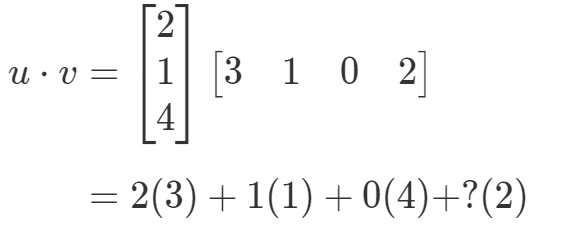
ここで問題が発生しました。 最初の3つの項目には掛け合わせるべき対応する項目があるが、最後の項目にはない。 では、ここでどうすればいいのでしょうか。 答えは、ここでは何もできないです。 これは、これらの 2 つのベクトルの内積を計算できないことを意味します。
つまり結論として、エントリの数が異なる 2 つのベクトルの内積を求めることはできないのです。
2×2 Matrix Multiplication
では、ドットプロダクトを学ぶ意味は何だったのでしょうか。 さて、内積を使うのは、2つの行列を掛け合わせるときです。 行列と別の行列を掛け合わせるとき、行と列をベクトルとして扱いたいのです。 具体的には、1つ目の行列の各行をベクトルとして、2つ目の行列の各列をベクトルとして扱いたいのです。
Question 3: A∙BA \bullet BA∙B if
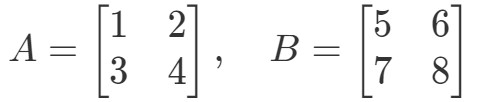
二つの行列を乗算すると、以下のようになります:
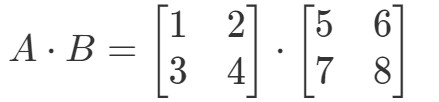
ここで注目する行と列は

ここで、r1r_{1}r1が1行目、r2r_{2}r2が2行目、c1、c2c_{1}、c_{2}c1、c2が1列目、2列目である。
ここで、2×2行列に別の2×2行列を掛けると、2×2行列になることに注意してください。
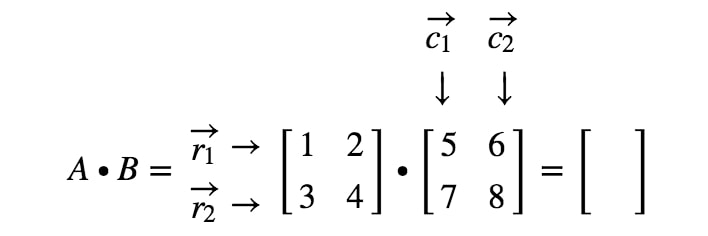
最初のエントリはどのように正確に得るのでしょうか。 さて、最初のエントリは、最初の行と列に位置していることに注意してください。 そこで、r1r_{1}r1とc1c_{1}c1の内積を取ればいいのです。 したがって、最初のエントリは
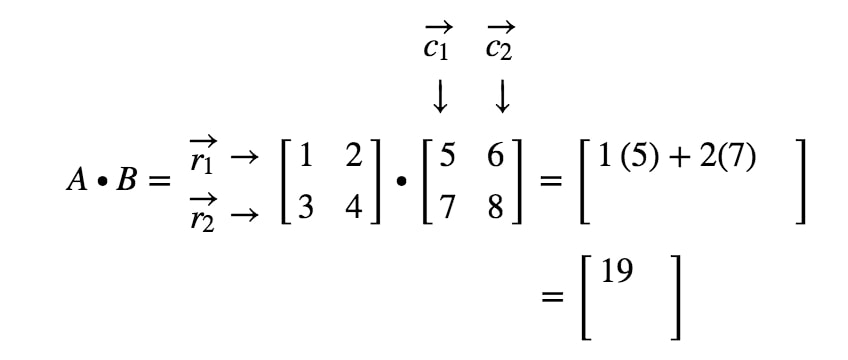
今回、2番目のエントリはどうすれば得られるでしょうか。 さて、2番目のエントリの位置は1行2列目であることに注目しましょう。 そこで、単純にr1r_{1}r1とc2c_{2}c2の内積を取ればよいのです。 したがって、2番目のエントリは
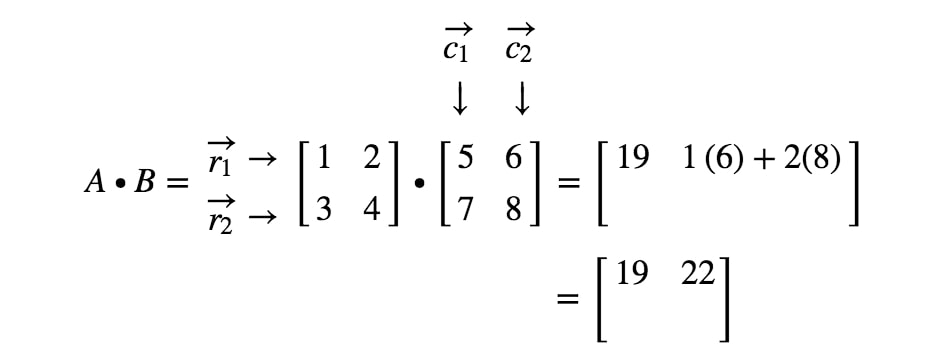
今度は同じ方法を使って、最後の2エントリを探します。 2つ目の最後のエントリは 2nd2^{nd}2nd 行と 1st1^{st}1st 列にあり、最後のエントリは 2nd2^{nd}2nd 行と 2nd2^{nd}2nd 列にあることに注意してください。 そこで、r2r_{2}r2とc1c_{1}c1の内積と、r2r_{2}r2とc2c_{2}c2の内積をとります。
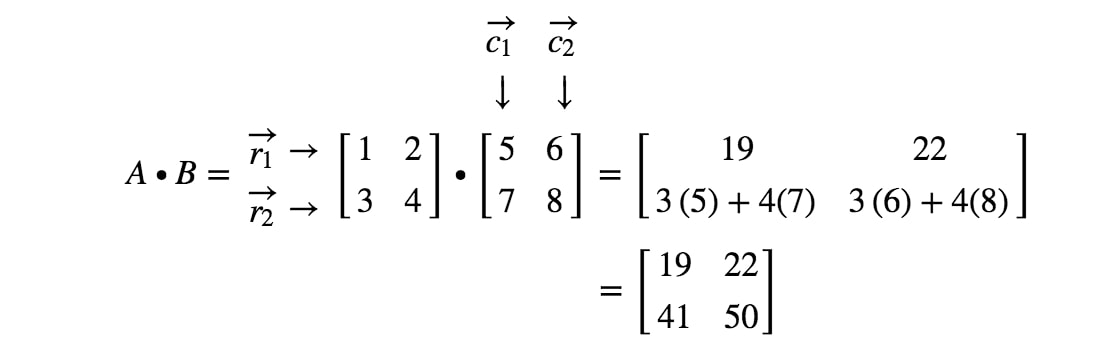
さて、これで完成です!
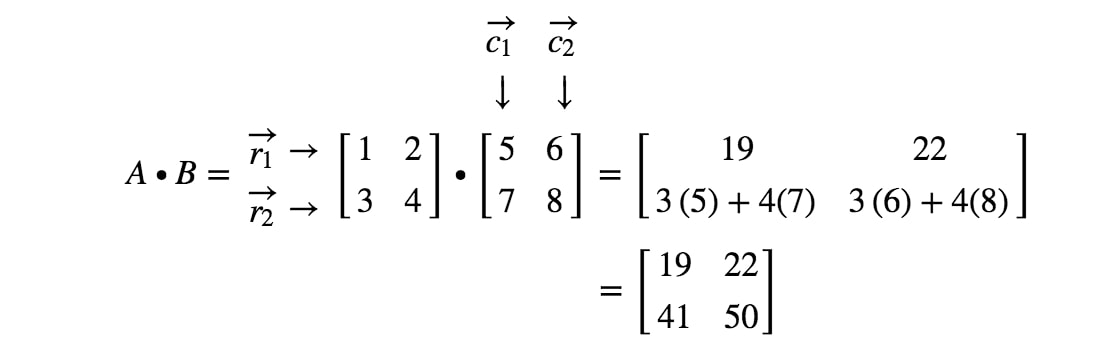 Equation 5: 2 x 2 Matrix Multiplication Example pt.7
Equation 5: 2 x 2 Matrix Multiplication Example pt.7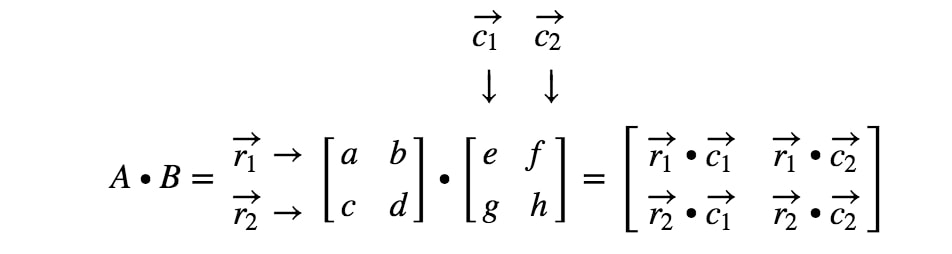
3×3行列乗算
さて3×3行列乗算は2×2行列乗算と非常に似た処理をしていますね。 3274>
Question 4:Find A∙BA \bullet BA∙B if
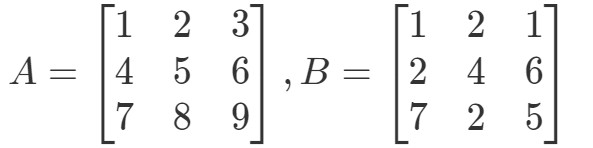
まず、掛けると別の3 x 3 matrixになることに注意してください。 つまり、
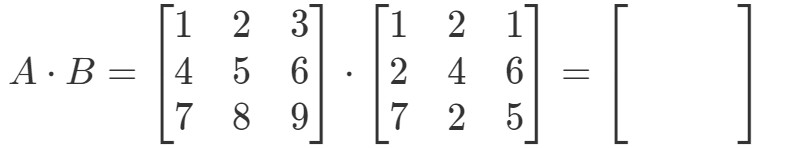
ここで、最初の行列の行と2番目の行列の列にラベルを付けます。
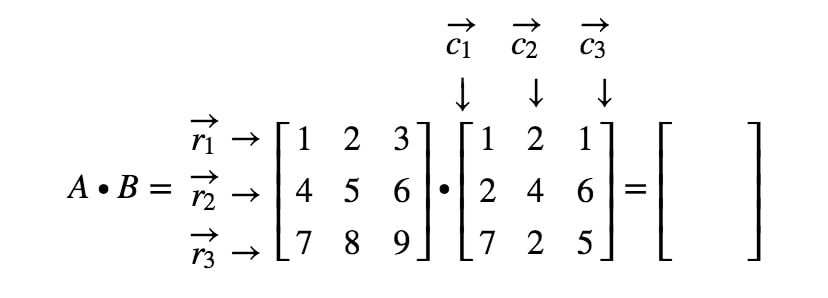
行列の最初のエントリは1^{st}1行目と1^{st}1列目にあることに注意して、r1r_{1}r1とc1c_{1}c1の内積を取ります。
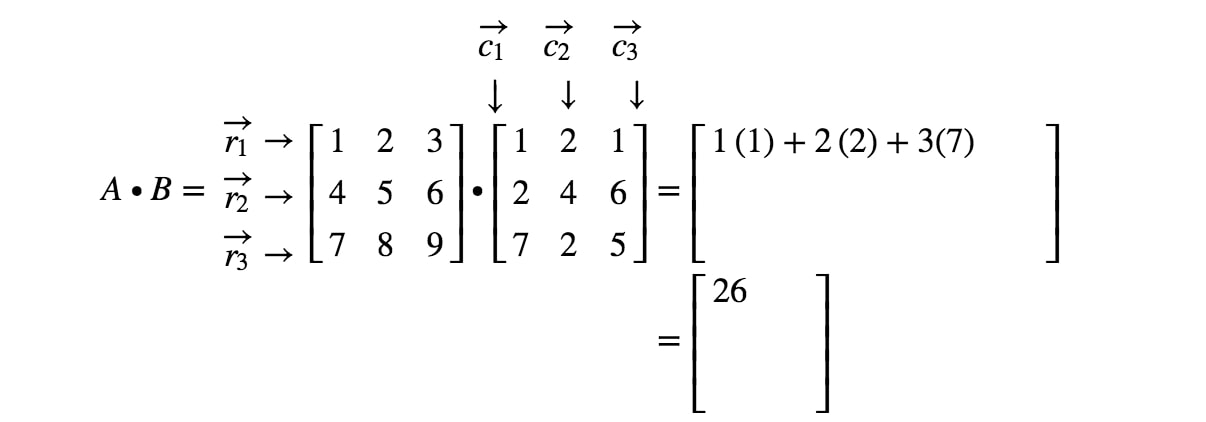
ここで、行列の2番目のエントリは1^{st}1行目と2^{nd}2列目にあることに注目しましょう。 したがって、r1r_{1}r1とc2c_{2}c2の内積をとります。
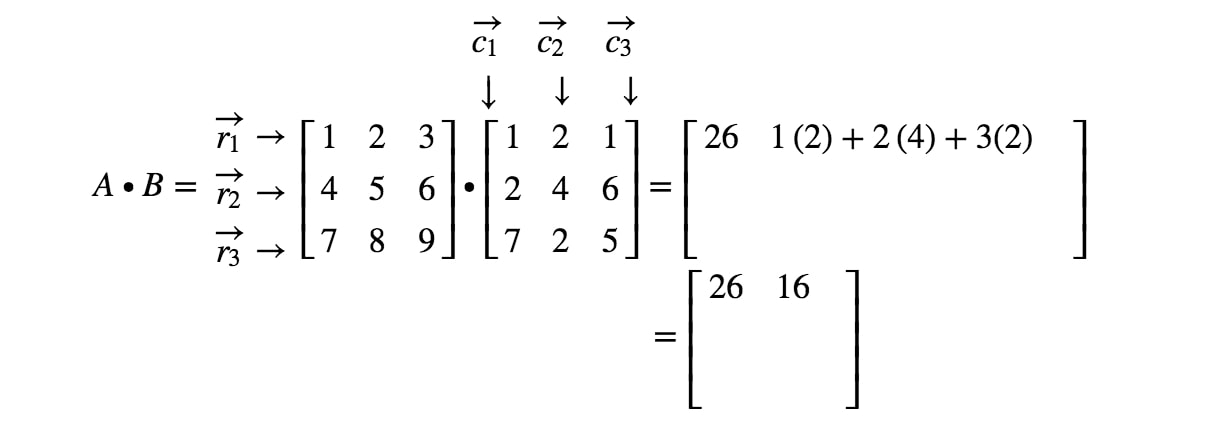
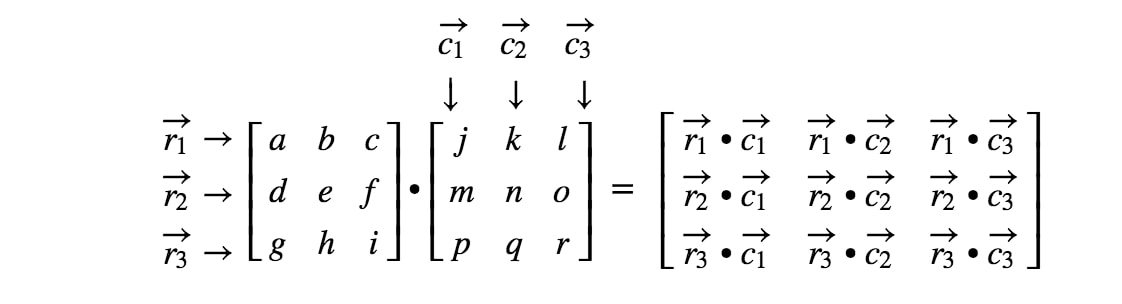
すべてのエントリの位置を確認し、行と列に対応するドット積を実行し続けると、最終的な結果が得られます。 行列が大きくなればなるほど、行列の掛け算は面倒になることに注意してください。 これは、より多くの数を扱わなければならないからです! 一般に、3×3の行列の乗算式は
異なる寸法の行列の乗算方法
ここまでは、同じ寸法の行列の乗算を説明しました。 また、同じ次元の2つの行列を乗算すると、同じ次元の行列が得られることも知っています。 しかし、異なる次元の行列を掛けるとどうなるのでしょうか。 計算された行列の次元はどのようにしてわかるのでしょうか? まず、行列を掛けると定義された行列が得られることを確認する必要があります。
行列は定義されているか
2つの行列を掛け合わせることができない場合があります。 そのような場合、その行列を未定義と呼びます。 未定義かどうかはどのように判断すればよいのでしょうか。
2つの行列の積は、最初の行列の列の数が2番目の行列の行の数と等しい場合にのみ定義されます。
この定義をこの例で使ってみましょう。
問題5: Let
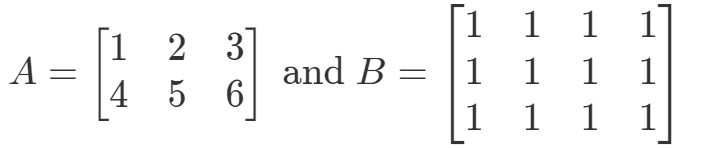
A・BAは定義されているか?
まず、最初の行列は3列であることに注目してください。 また、2番目の行列には3つの行があります。
定義されていることがわかったところで、A∙BA∙BA∙Bの次元はどのようにしてわかるのでしょうか?
次元の性質
A∙BA∙B の次元を知るには、まずandの次元を別々に調べます。
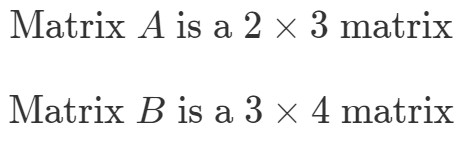
ここで、行列の次元を並べてみます。
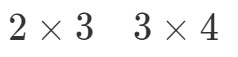
これから行うことは、最初の数字と最後の数字を取り、それを組み合わせてA・BAの寸法を得ることです。 最初の数字が2で最後の数字が4であることがわかります。したがって、A∙BA ∙BA ∙Bの次元は次のようになります:
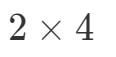
行列の次元がわかったので、ドットプロダクトを使って各項目を計算できます。
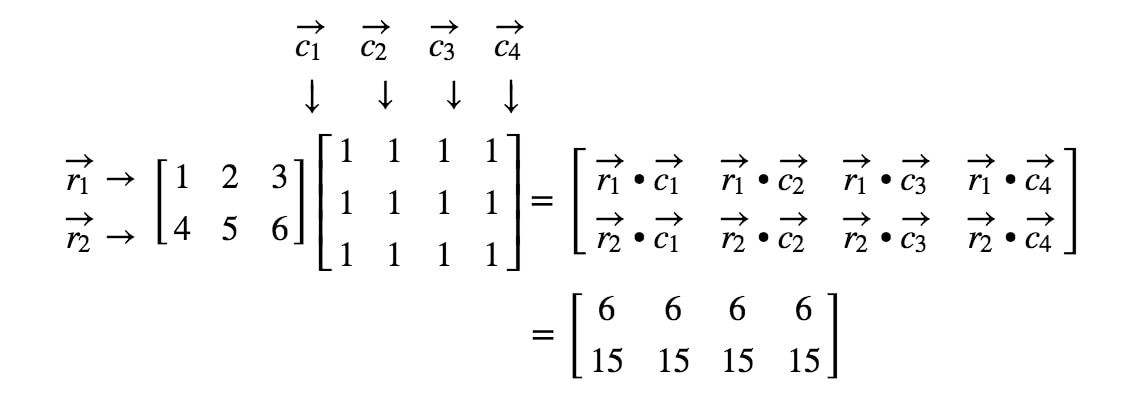
さて、行列の掛け算がよくわかったところで、行列の掛け算の法則を見ていきましょう。
X,Y,ZX,Y,ZX,Y,Zを行列、InI_{n}Inを単位行列、OnO_{n}Onをゼロ行列としましょう。 これらの5つの行列がすべて等しい次元であれば、次のような行列同士の乗算の性質があります:

連想特性は、乗算する順序は関係ないことを示しています。 つまり、X・YX Ⓐ YX・Y を計算してから ZZZ をかけても、Y・ZY Ⓐ ZY・Z を計算してから XXX をかけても同じ結果になるのです。
Question 6: Associative Property がこれらの行列で機能することを示せ:

連想特性の式の左辺を見ると、(XY)Z(XY)Zで:
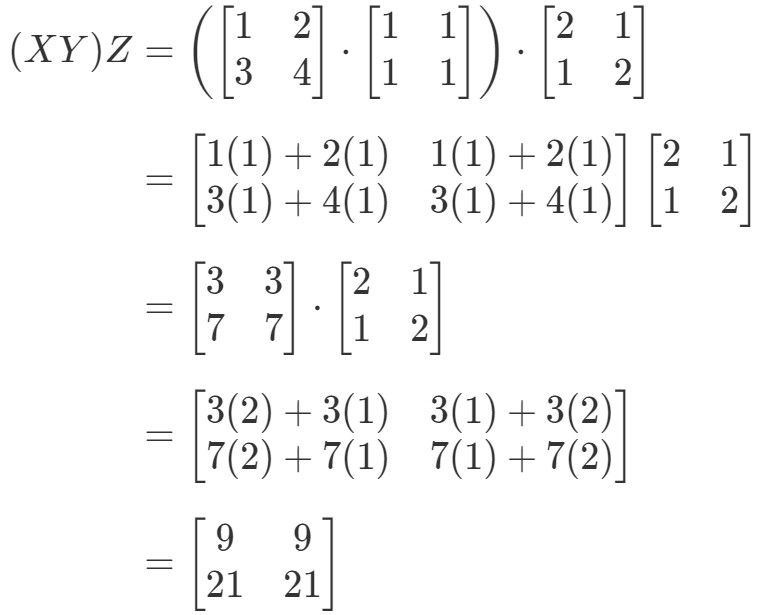
ここで、連想特性の式の右辺を見てみると、X(YZ)X(YZ)X(YZ)から:
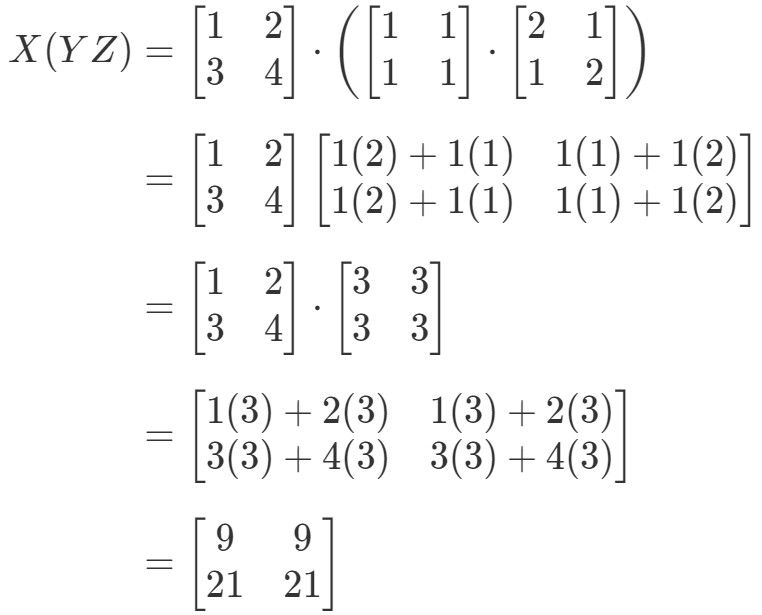
左辺、右辺ともに同じになっていることを確認することができる。 したがって、連想性が実際に働いていることがわかりますね。 繰り返しますが、これは行列の乗算順序が重要でないことを意味します!
さて、次の性質は「分配的性質」です。
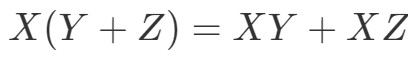
行列に対しても箔付けの手法が許されることが分かります。
Question 7: 分配的性質が次の行列に対して働くことを示しなさい:

式の左辺は X(Y+Z)X(Y + Z)X(Y+Z) となることを確認しなさい。 したがって、これを計算すると、
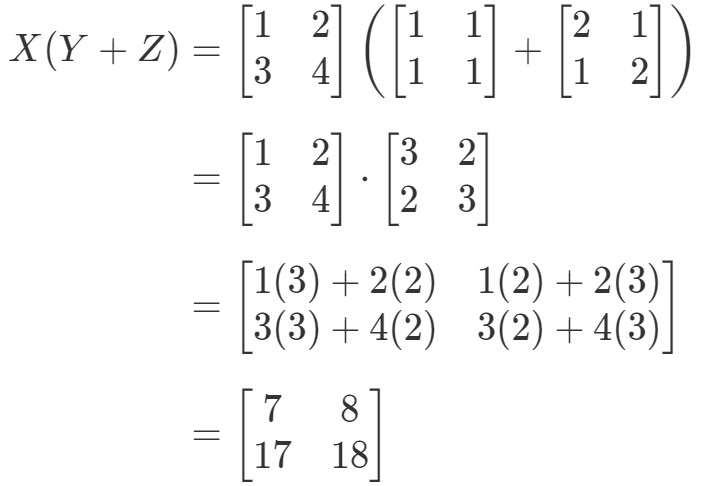
ここで、式の右辺が全く同じものを与えているかどうかを確認してみましょう。 式の右辺はXY+XZXY+XZであることに注目しましょう。 これを計算すると、
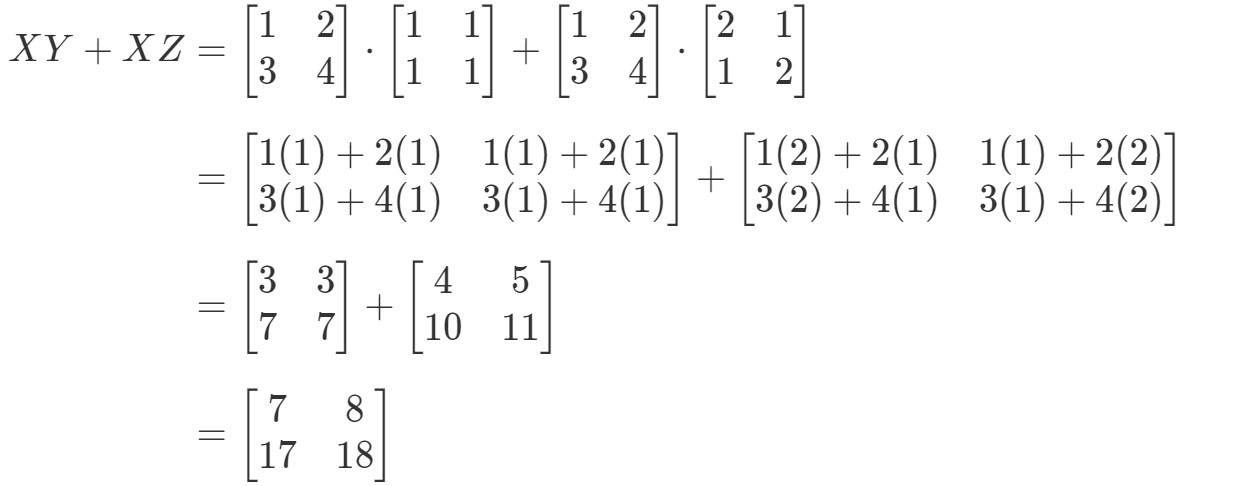
式の左辺が右辺と全く同じであることに注意してください。
行列の掛け算は可換か
行列の掛け算は連想性と分配性の両方を満たすことが分かっていますが、可換性については全く触れませんでしたね。 行列の乗算はこれを満たさないということでしょうか。
Question 8: もし行列の乗算が可換であれば、次のことが成り立つはずです:
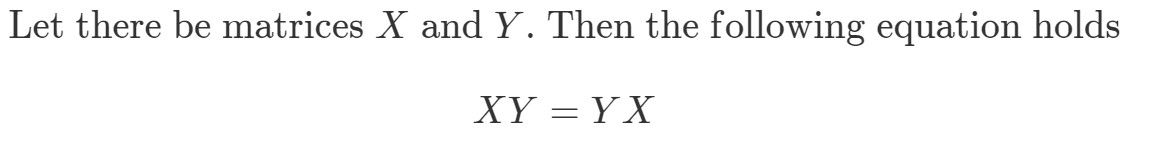
以下の場合、XYeqYXXY eq YXXYeqYX を示す。
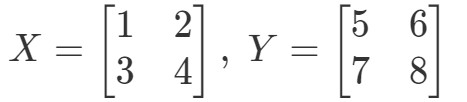
最初に式の左辺を計算する。 XYXYを計算すると:
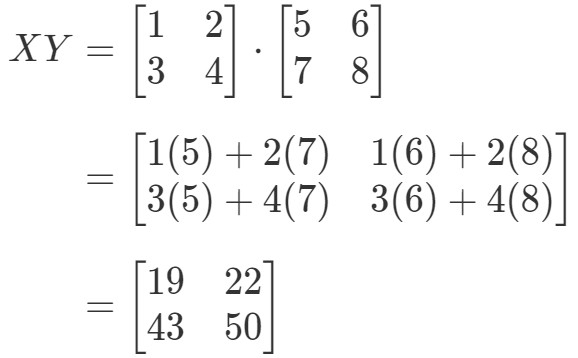
ここで式の右辺を計算すると:
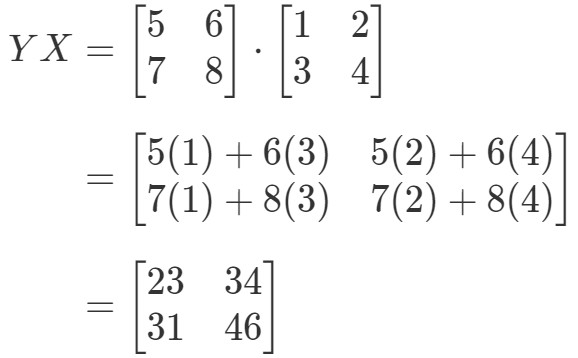
このように、
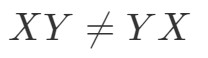
このように
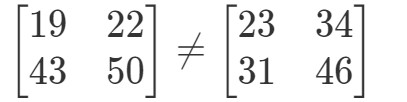
この二つの行列は全く違います。
さて、行列の乗法の性質はまだ少し残っていますね。 しかし、これらの性質はゼロ行列と単位行列を扱います。
ゼロ行列に対する行列の乗算
ゼロ行列に対する行列の乗算性質は次のように述べています:
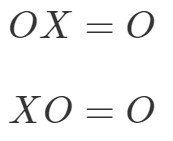
ここでOOOはゼロ行列であり、OOはゼロ行列です。
これは、ゼロの行列と別のゼロでない行列を掛け合わせると、ゼロの行列ができることを意味しています。
Question 9: 式OX=OOX=O、XO=OXO=Oが成り立つのは、次の場合であることを示しなさい:
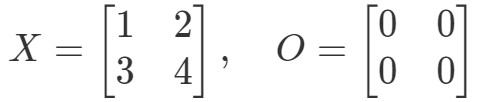
まず式を見てみましょう
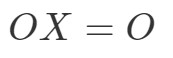
OXOXを計算すると、
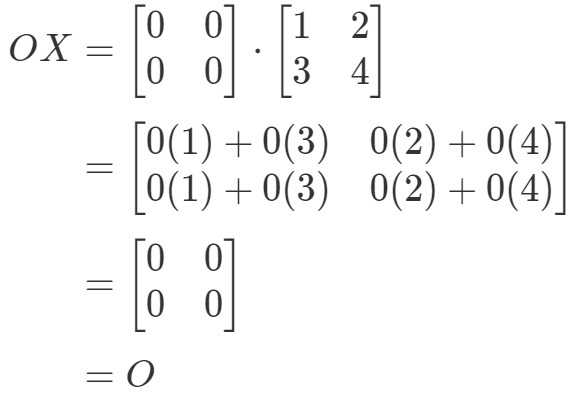
確かにOX=OOX=Oですから式は成立していますね。 同様にXOXOXOを計算すると、
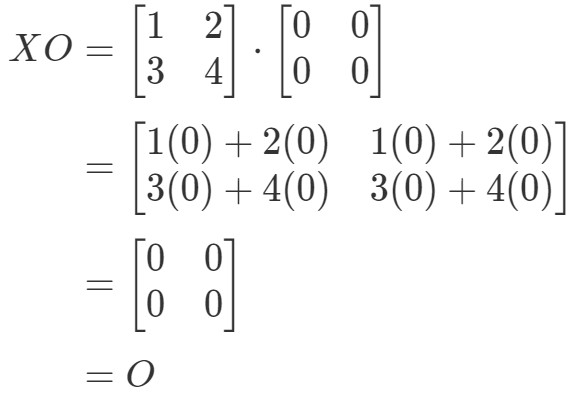
式XO=OXO=Oが成り立つことがわかりましたので、終了です。
単位行列の行列の乗算
さて、単位行列の行列乗算特性はどうなっているでしょうか。 さて、その性質とは次のようなものです:
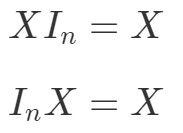
ここでInI_{n}Inはn×nn倍のn×n恒等行列であり、この行列の行列乗算は次のようになります。 3274>
問題10 XI2=XX I_{2} = XXI2=X と I2X=XI_{2} の式が成り立つことを示せ。 X = XI2X=X が次の行列で成り立つ
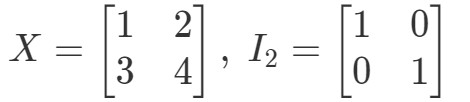
したがって、式XI2=XX I_{2} = XXI2=Xに対して、
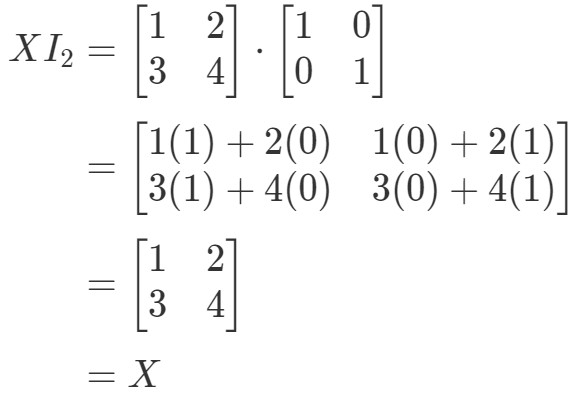
式は成立することになるわけです。 I2X=XI_{2}X = XI2X=Xという式と同様に、:
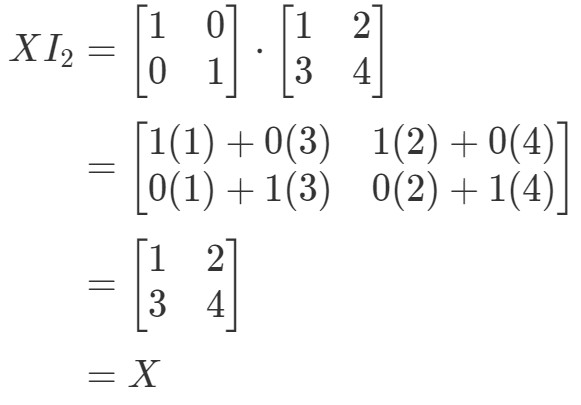
この場合も方程式は成り立ちますね。 これで、行列の乗算の性質はすべて終了です。 さて、行列の掛け算の実際の応用を見たい方は、こちらの記事をご覧ください。
https://www.mathsisfun.com/algebra/matrix-multiplying.html