Free Press

Înmulțirea matricelor

Există exact două moduri de înmulțire a matricelor. Primul mod este de a înmulți o matrice cu un scalar. Aceasta este cunoscută sub numele de înmulțire scalară. Al doilea mod este de a înmulți o matrice cu o altă matrice. Aceasta este cunoscută sub numele de înmulțire matriceală.

Înmulțirea scalară

înmulțirea scalară este de fapt o operație matriceală foarte simplă. Pentru a înmulți un scalar cu o matrice, pur și simplu luăm scalarul și îl înmulțim cu fiecare intrare din matrice. Să dăm un exemplu.

Întrebare 1: Calculați 2A2A2A dacă

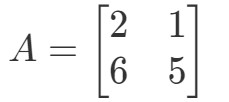
Întrebarea ne cere să aflăm ce este 2A2A2A. Cu alte cuvinte, aflăm

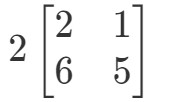
Observați că dacă vom înmulți 2 la fiecare intrare din matrice, obținem că:

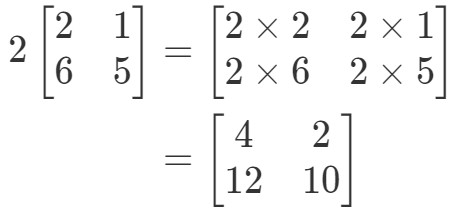
Mult simplu! Să mai facem una.

Întrebarea 2: Calculați 0A0A0A dacă

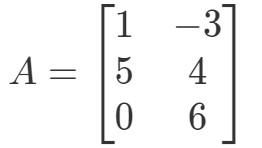
Din nou, încercăm să găsim 0A0A0A0A. Acest lucru înseamnă că vom căuta răspunsul la

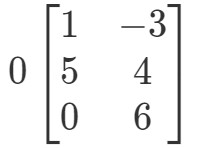
Matricea va avea o formă ciudată, dar conceptul rămâne același. Vom multiplica în continuare scalarul 0 la fiecare intrare din matrice. Procedând astfel obținem:

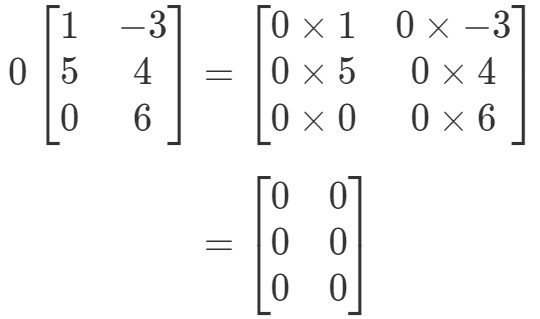
Observați că toate intrările din matrice sunt 0. Aceasta este cunoscută sub numele de matrice zero care este 3 x 2.

Acum că suntem foarte familiarizați cu înmulțirea scalară, de ce să nu trecem la înmulțirea matricelor?

Cum se înmulțesc matricile

Pentru a înmulți o matrice cu o altă matrice, trebuie mai întâi să învățăm ce este produsul punctual.

Ce este produsul punctual?

Produsul punctual (cunoscut și sub numele de înmulțire vectorială) este o modalitate de a calcula produsul a doi vectori. De exemplu, fie cei doi vectori:

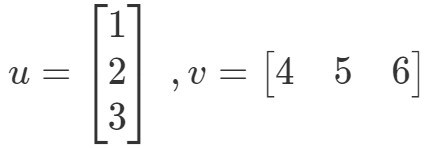
Cum aș putea înmulți acești doi vectori? Pur și simplu trebuie doar să înmulțim intrările corespunzătoare și să adunăm produsele. Cu alte cuvinte,

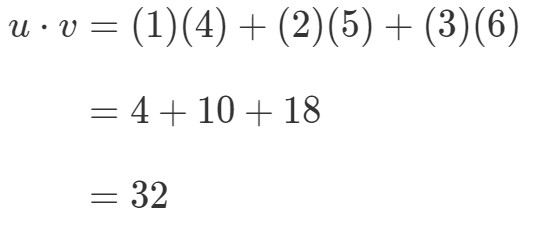
Acum obținem o singură valoare din înmulțirea vectorilor. Totuși, observați cum că cei doi vectori au același număr de intrări. ce se întâmplă dacă unul dintre vectori are un număr diferit de intrări față de celălalt? De exemplu, fie

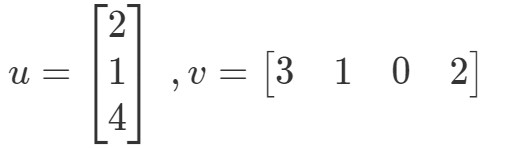
Dacă ar fi să înmulțesc intrările corespunzătoare și să le adun pe toate împreună, atunci obțin:

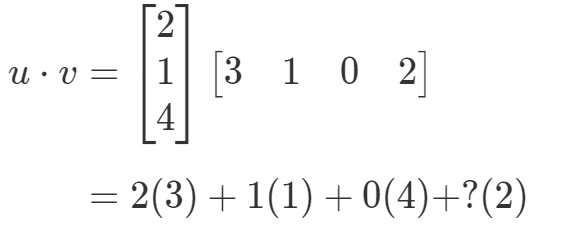
Există o problemă aici. Primele trei intrări au intrări corespunzătoare cu care să se înmulțească, dar ultima intrare nu are. Deci, ce facem aici? Răspunsul este că nu putem face nimic aici. Acest lucru înseamnă doar că nu putem calcula produsul în puncte al acestor doi vectori.

În concluzie, nu putem găsi produsul în puncte a doi vectori care au numere diferite de intrări. Ei trebuie să aibă același număr de intrări.

Multiplicare matricială 2 x 2

Atunci ce rost a avut învățarea produsului punct? Ei bine, vom folosi produsul punctat atunci când vom înmulți două matrici împreună. Atunci când înmulțim o matrice cu o altă matrice, dorim să tratăm rândurile și coloanele ca pe un vector. Mai exact, dorim să tratăm fiecare rând din prima matrice ca pe un vector, iar fiecare coloană din a doua matrice ca pe un vector. Să dăm un exemplu.

Întrebarea 3: Găsiți A∙BA \bullet BA∙B dacă

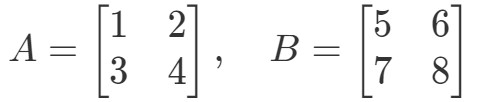
Multiplicând cele două matrici vom obține:

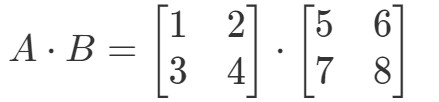
Acum rândurile și coloanele pe care ne concentrăm sunt

unde r1r_{1}r1 este primul rând, r2r_{2}r2 este al doilea rând și, c1,c2c_{1}, c_{2}c1,c2 sunt prima și a doua coloană. Acum vom trata fiecare rând și fiecare coloană pe care le vedem aici ca pe un vector.

Rețineți aici că înmulțind o matrice 2 x 2 cu o altă matrice 2 x 2 se obține o matrice 2 x 2. Cu alte cuvinte, matricea pe care o obținem ar trebui să aibă 4 intrări.

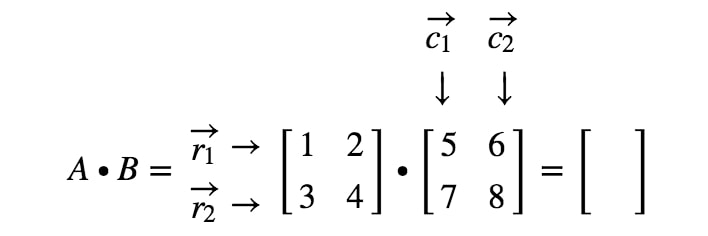
Cum obținem exact prima intrare? Ei bine, observați că prima intrare se află pe primul rând și prima coloană. Așadar, luăm pur și simplu produsul punctelor dintre r1r_{1}r1 și c1c_{1}c1. Astfel, prima intrare va fi

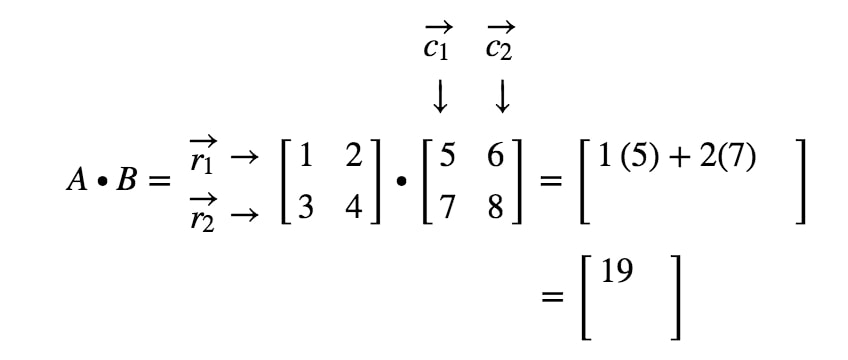
Cum obținem a doua intrare de data aceasta? Ei bine, observați că locația celei de-a doua intrări este în primul rând și a doua coloană. Așa că pur și simplu luăm produsul punctelor dintre r1r_{1}r1 și c2c_{2}c2. Astfel, a doua intrare va fi

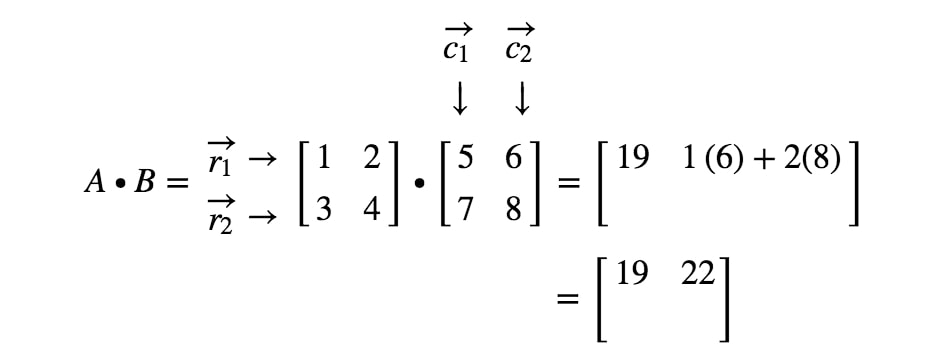
Acum vom folosi aceeași strategie pentru a căuta ultimele două intrări. Observați că penultima intrare este localizată în al 2-lea2^{nd}2-lea rând și în prima1^{st}1-a coloană, iar ultima intrare este localizată în al 2-lea2^{nd}2-lea rând și a 2-a2^{nd}2-a coloană. Așadar, luăm produsul în puncte dintre r2r_{2}r2 și c1c_{1}c1 și produsul în puncte dintre r2r_{2}r2 și c2c_{2}c2. Acest lucru ne dă:

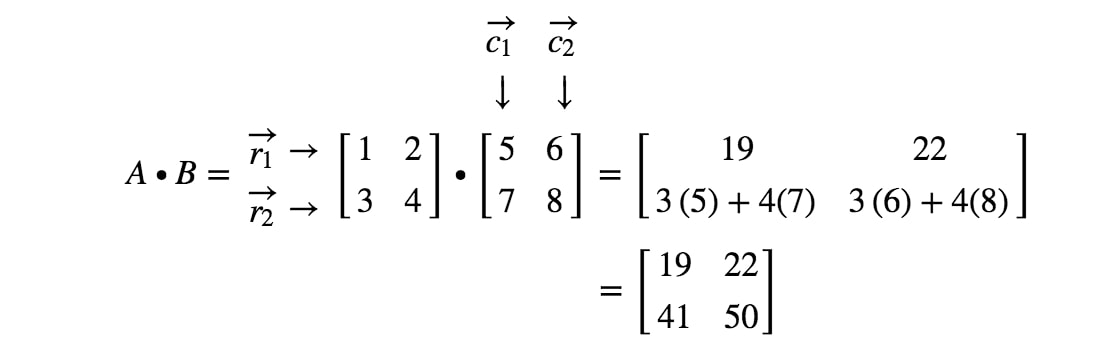
Acum am terminat! Iată ce obținem atunci când înmulțim 2 x 2 matrici. În general, formula de înmulțire a matricelor 2 x 2 este

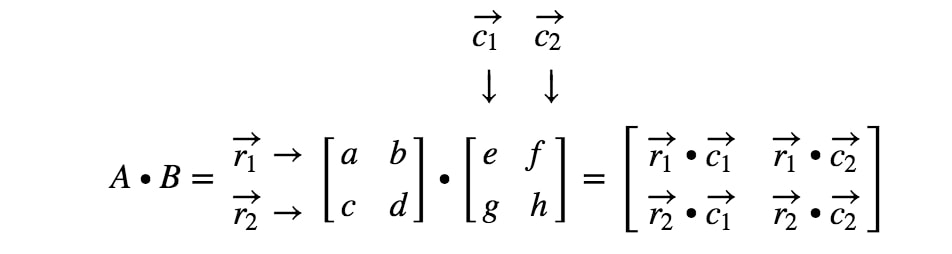
Multiplicare a matricelor 3 x 3

Acum, procesul de înmulțire a matricelor 3 x 3 este foarte asemănător cu procesul de înmulțire a matricelor 2 x 2. Din nou, de ce să nu facem un exemplu de înmulțire a matricelor?

Întrebarea 4:Găsiți A∙BA \bullet BA∙B dacă

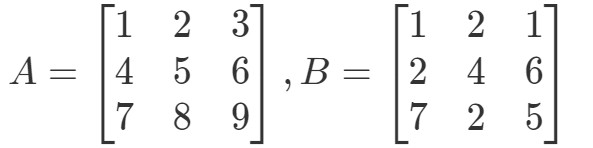
În primul rând, observați că înmulțirea acestora ar trebui să ne dea o altă matrice 3 x 3. Cu alte cuvinte,

Acum să etichetăm toate rândurile noastre din prima matrice și coloanele din a doua matrice.

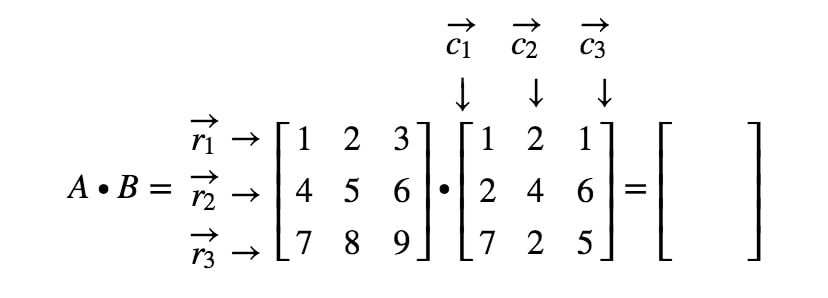
Observați că prima intrare a matricei este situată în primul1^{st}1 rând și prima1^{st}1 coloană, așa că luăm produsul în puncte al lui r1r_{1}r1 și c1c_{1}c1. Acest lucru ne dă:

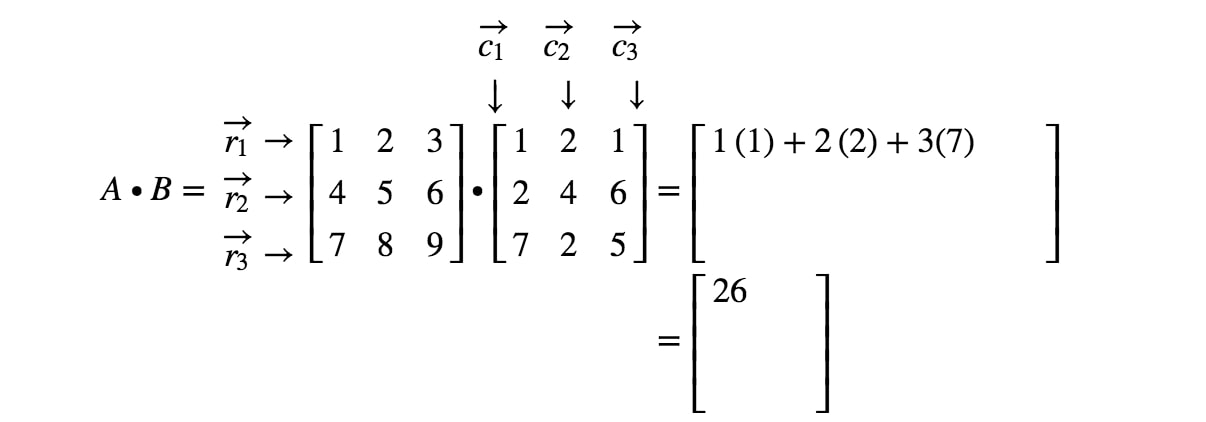
Acum observați că a doua intrare a matricei este situată în primul1^{st}1lea rând și al 2-lea2^{nd}2lea coloană. Astfel, luăm produsul punctelor dintre r1r_{1}r1 și c2c_{2}c2. Acest lucru ne dă:

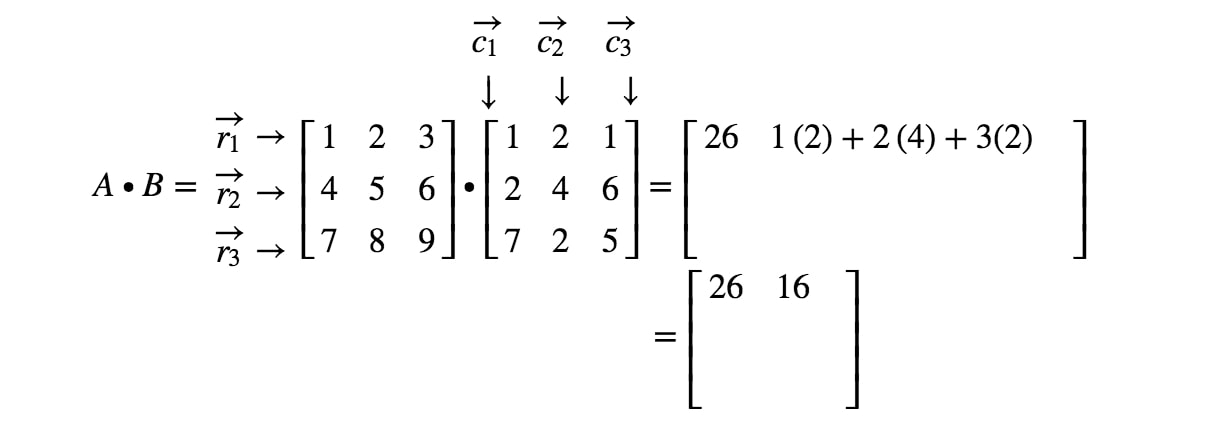
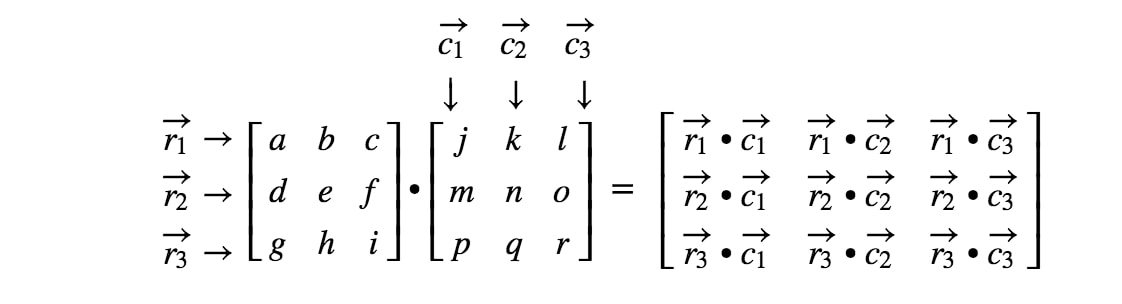
Dacă vom continua să localizăm toate intrările și să facem produsul punctelor corespunzător rândurilor și coloanelor, atunci obținem rezultatul final:

Am terminat! Observați că, cu cât matricile sunt mai mari, cu atât multiplicarea matricelor devine mai plictisitoare. Acest lucru se datorează faptului că trebuie să avem de-a face cu tot mai multe numere! În general, formula de înmulțire a matricelor pentru matrici 3 x 3 este

Cum se înmulțesc matrici cu dimensiuni diferite?

Până acum am înmulțit matrici cu aceleași dimensiuni. În plus, știm că înmulțirea a două matrici cu aceeași dimensiune dă o matrice de aceleași dimensiuni. Dar ce se întâmplă dacă înmulțim o matrice cu dimensiuni diferite? Cum am putea ști care sunt dimensiunile matricei calculate? În primul rând, trebuie să vedem că înmulțirea matricelor dă o matrice definită.

Este matricea definită?

Există cazuri în care nu este posibilă înmulțirea a două matrici împreună. Pentru aceste cazuri, se spune că matricea este nedefinită. Cum ne putem da seama dacă sunt nedefinite?

Produsul a două matrici este definit doar dacă numărul de coloane din prima matrice este egal cu numărul de rânduri din cea de-a doua matrice.

Să încercăm să folosim această definiție în acest exemplu.

Întrebarea 5: Fie

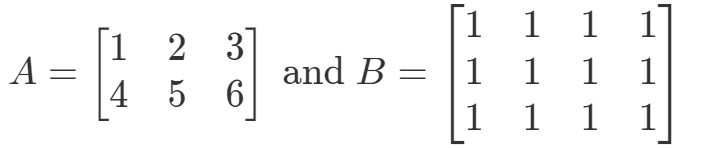
Este A∙BA \bullet BA∙B definit?

În primul rând, observați că prima matrice are 3 coloane. De asemenea, a doua matrice are 3 rânduri. Deoarece ambele sunt egale cu 3, atunci știu că A∙BA \bullet BA∙B este definită.

Acum că știm că este definită, cum am putea ști care sunt dimensiunile lui A∙BA \bullet BA∙B?

Proprietatea dimensiunilor

Pentru a afla dimensiunile lui A∙BA \bullet BA∙B, trebuie să ne uităm mai întâi la dimensiunile lui și separat.

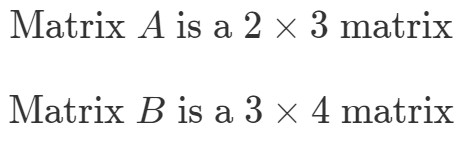
Acum vom pune dimensiunile matricelor una lângă alta astfel:

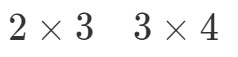
Ceea ce vom face acum este să luăm primul număr și ultimul număr și să le combinăm pentru a obține dimensiunile lui A∙BA \bullet BA∙B. Vedeți că primul număr este 2 și ultimul număr este 4. Deci, dimensiunile lui A∙BA \bullet BA∙B vor fi:

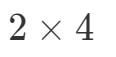
Acum că știm dimensiunile matricei, putem calcula fiecare intrare folosind produsele punctiforme. Acest lucru ne va da:

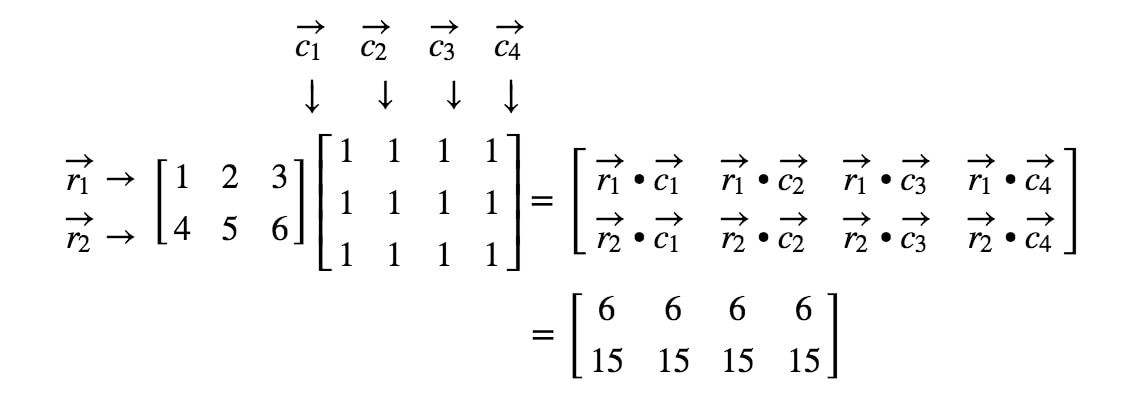
Acum că știm foarte bine cum să înmulțim matrici, de ce să nu aruncăm o privire la câteva reguli de înmulțire a matricelor?

Proprietăți ale înmulțirii matricelor

Acum, ce tip de proprietăți are de fapt înmulțirea matricelor? Mai întâi, să definim formal totul.

Să fie X, Y, ZX, Y, Y, ZX, Y, ZX, Y, Z matrici, InI_{n}In să fie o matrice identitate și OnO_{n}On să fie o matrice zero. Dacă toate aceste cinci matrici au dimensiuni egale, atunci vom avea următoarele proprietăți de înmulțire de la matrice la matrice:

Proprietatea asociativă afirmă că ordinea în care se înmulțește nu contează. Cu alte cuvinte, calculând X∙YX \bullet YX∙Y și apoi înmulțind cu ZZZ veți obține același rezultat ca și calculând Y∙ZY \bullet ZY∙Z și apoi înmulțind cu XXX. Să facem un exemplu.

Întrebare 6: Arătați că proprietatea asociativă funcționează cu aceste matrici:

Urmărind partea stângă a ecuației din proprietatea asociativă, vedem că (XY)Z(XY)Z(XY)Z(XY)Z dă:

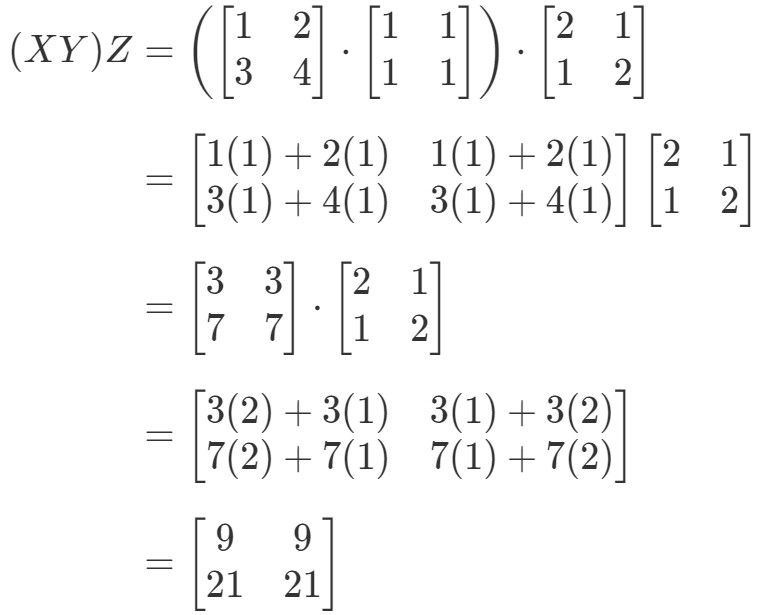
Acum, uitându-ne la partea dreaptă a ecuației din proprietatea asociativă, vedem că X(YZ)X(YZ)X(YZ) dă:

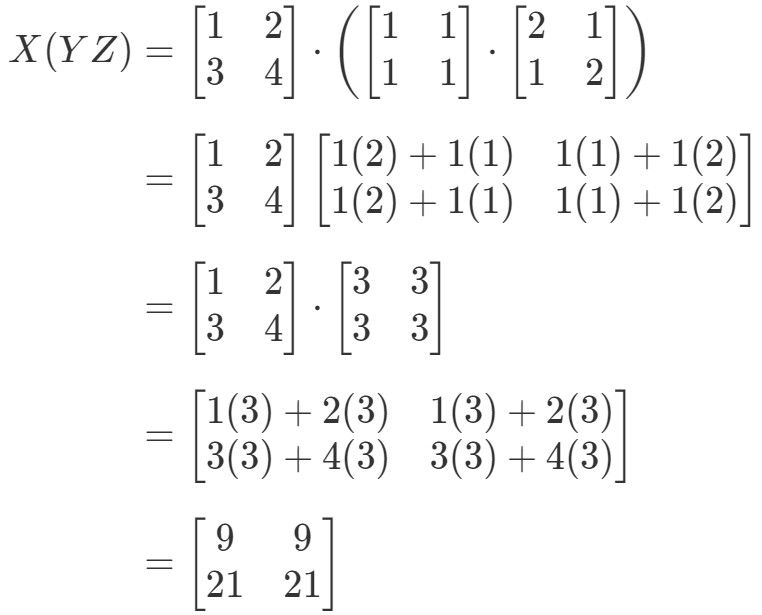
Vezi cum partea stângă și partea dreaptă a ecuației sunt ambele egale. Prin urmare, știm că proprietatea asociativă chiar funcționează! Din nou, acest lucru înseamnă că ordinea de înmulțire a matricei nu contează!

Acum, următoarea proprietate este proprietatea distributivă. Proprietatea distributivă afirmă că:

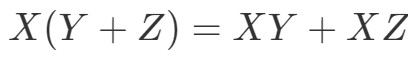
Vezi că ne este permis să folosim tehnica foii și pentru matrici. Pentru a arăta că această proprietate funcționează, să facem un exemplu.

Întrebare 7: Arătați că proprietatea distributivă funcționează pentru următoarele matrici:

Vezi că partea stângă a ecuației este X(Y+Z)X(Y+Z)X(Y+Z)X(Y+Z). Prin urmare, calculând asta ne dă:

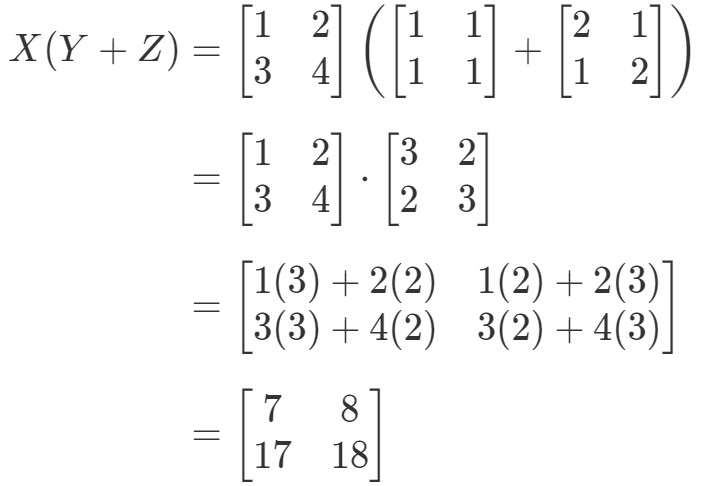
Acum să verificăm dacă partea dreaptă a ecuației ne dă exact același lucru. Observați că partea dreaptă a ecuației este XY+XZXY + XZXY+XZ. Calculând acest lucru ne dă:

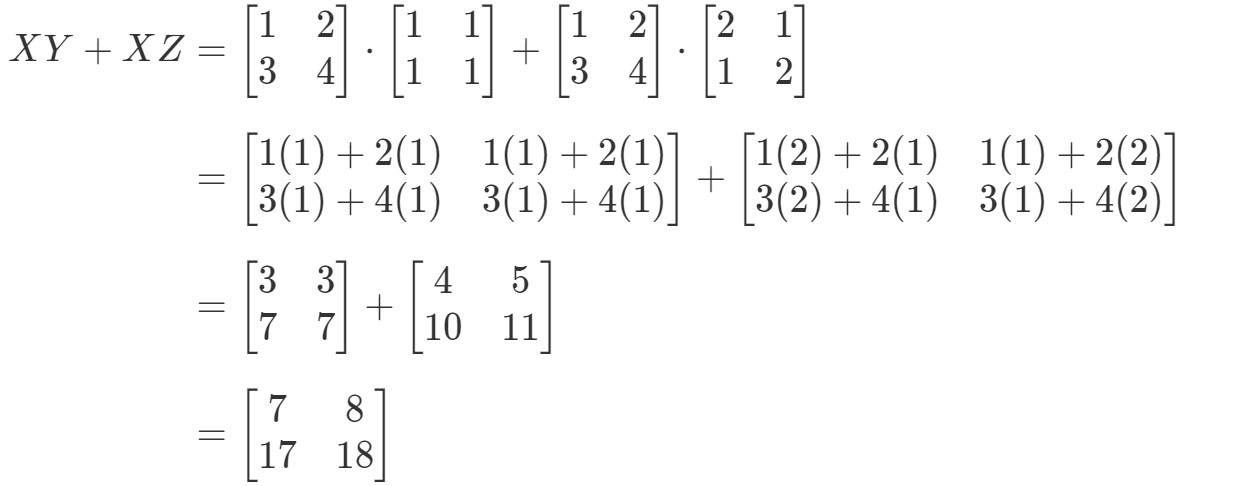
Observați că partea stângă a ecuației este exact aceeași cu partea dreaptă a ecuației. Prin urmare, putem confirma că proprietatea distributivă chiar funcționează.

Înmulțirea matricelor este comutativă?

Știm că înmulțirea matricelor satisface atât proprietățile asociativă cât și distributivă, însă nu am vorbit deloc despre proprietatea comutativă. Înseamnă asta că înmulțirea matricelor nu o satisface? De fapt, nu o face și putem verifica acest lucru cu un exemplu.

Întrebarea 8: Dacă înmulțirea matricelor este comutativă, atunci următoarele trebuie să fie adevărate:

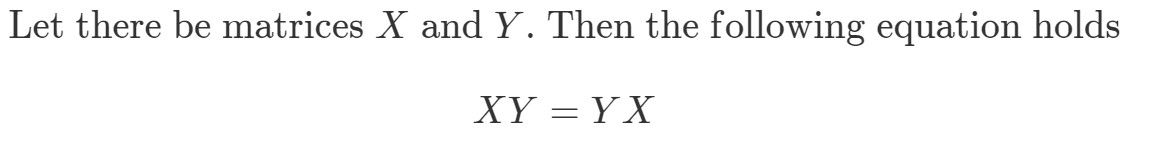
Demonstrați că XYeqYXXY eq YXXYeqYX dacă

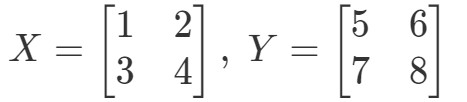
În primul rând calculăm partea stângă a ecuației. Calculând XYXYXYXYXY ne dă:

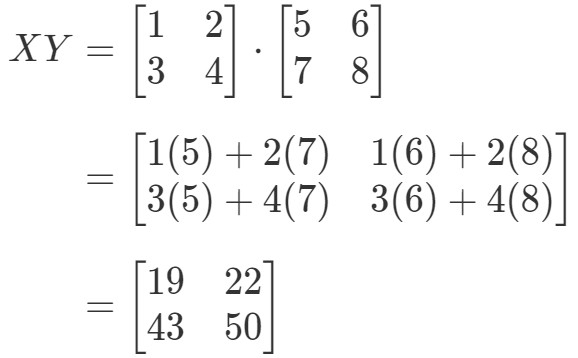
Calculând acum partea dreaptă a ecuației, avem:

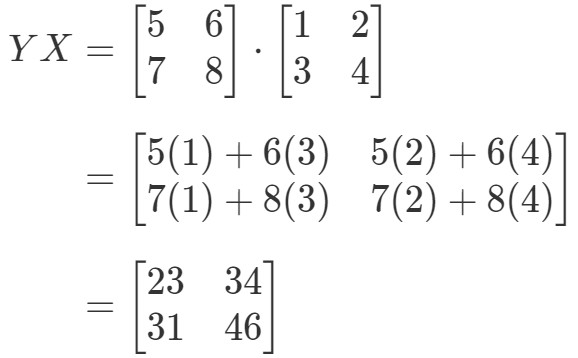
Cum se poate vedea,

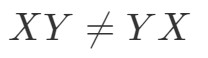
Pentru că avem

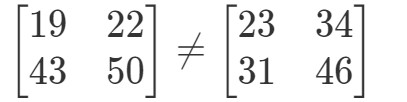
Aceste două matrici sunt complet diferite.

Acum mai sunt încă câteva proprietăți ale înmulțirii matricelor. Cu toate acestea, aceste proprietăți se referă la matricele zero și la matricele identitate.

Multiplicarea matricelor pentru matricea zero

Proprietatea de multiplicare a matricelor pentru matricea zero afirmă următoarele:

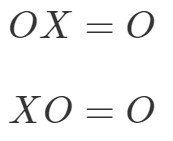
unde OOO este o matrice zero.

Acest lucru înseamnă că, dacă înmulțițiți o matrice zero cu o altă matrice diferită de zero, atunci veți obține o matrice zero. Să testăm dacă acest lucru este adevărat cu un exemplu.

Întrebare 9: Arătați că ecuația OX=OOX = OOX=O și XO=OXO = OXO=O este valabilă dacă:

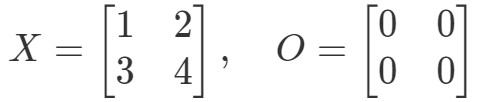
Să ne uităm mai întâi la ecuația

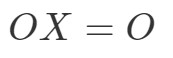
Observați că calculul OXOXOX ne dă:

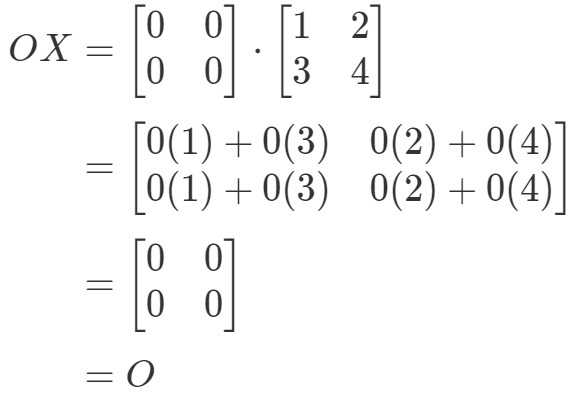
Vezi că OX=OOX = OOX=O, deci ecuația este valabilă. În mod similar, dacă calculăm XOXOXO, obținem:

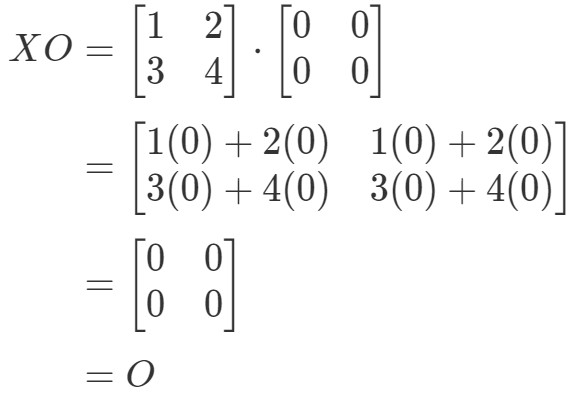
Vezi că ecuația XO=OXO = OXO=O ține, așa că am terminat.

Multiplicarea matricelor pentru matricea identitate

Cum rămâne cu proprietatea de multiplicare a matricelor pentru matrici identitate? Ei bine, proprietatea afirmă următoarele:

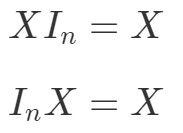
unde InI_{n}In este o matrice de identitate n×nn \ ori nn×n. Din nou, putem vedea că următoarele ecuații se susțin cu un exemplu.

Întrebare 10: Arătați că ecuațiile XI2=XX I_{2} = XXI2=X și I2X=XI_{2} X = XI2X = XI2X=X se susține cu următoarele matrici

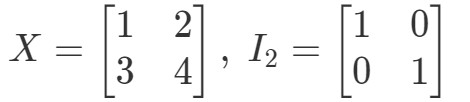
Atunci pentru ecuația XI2=XX I_{2} = XXI2=X, avem:

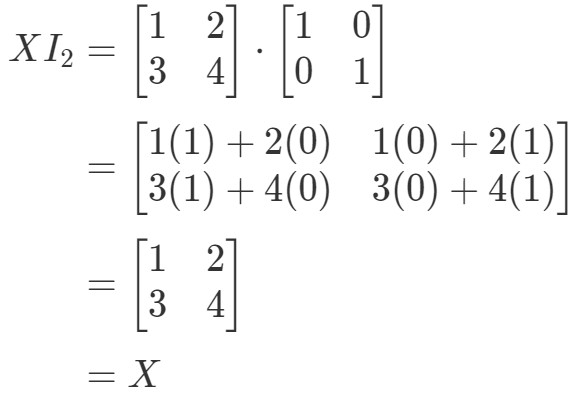
Atunci ecuația ține. Similar cu ecuația I2X=XI_{2}X = XI2X=X, avem:

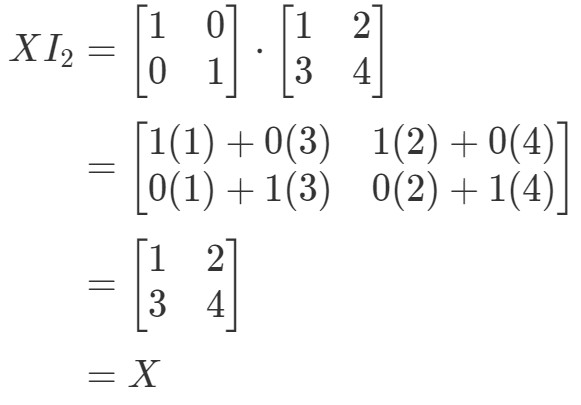
Din nou, ecuația se susține. Așadar, am terminat cu întrebarea și ambele ecuații se mențin. astfel se încheie toate proprietățile înmulțirii matricelor. Acum, dacă doriți să vedeți o aplicație din viața reală a înmulțirii matricelor, vă recomand să consultați acest articol.

https://www.mathsisfun.com/algebra/matrix-multiplying.html

https://www.mathsisfun.com/algebra/matrix-multiplying.html

.