Free Press

Matrismultiplikation

Det finns exakt två sätt att multiplicera matriser. Det första sättet är att multiplicera en matris med en skalär. Detta är känt som skalärmultiplikation. Det andra sättet är att multiplicera en matris med en annan matris. Detta är känt som matrismultiplikation.

Skalär multiplikation

Skalär multiplikation är faktiskt en mycket enkel matrisoperation. För att multiplicera en skalär med en matris tar vi helt enkelt skalären och multiplicerar den med varje post i matrisen. Låt oss göra ett exempel.

Fråga 1: Beräkna 2A2A2A om

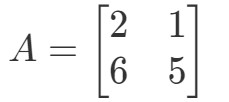
Frågan ber oss att ta reda på vad 2A2A2A är. Med andra ord ska vi ta reda på

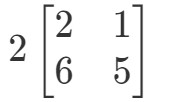
Observera att om vi multiplicerar 2 med varje post i matrisen får vi följande:

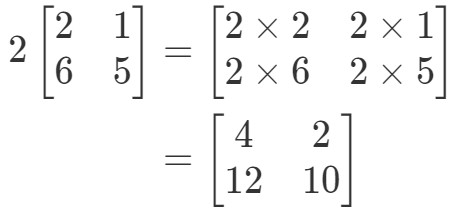
Väldigt enkelt! Låt oss göra en till.

Fråga 2: Beräkna 0A0A0A om

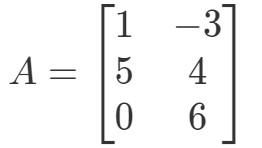
Ännu en gång försöker vi hitta 0A0A0A. Detta innebär att vi kommer att leta efter svaret på

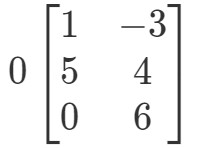
Matrisen kommer att ha en udda form, men konceptet förblir detsamma. Vi kommer fortfarande att multiplicera skalaren 0 med varje post i matrisen. Detta ger oss:

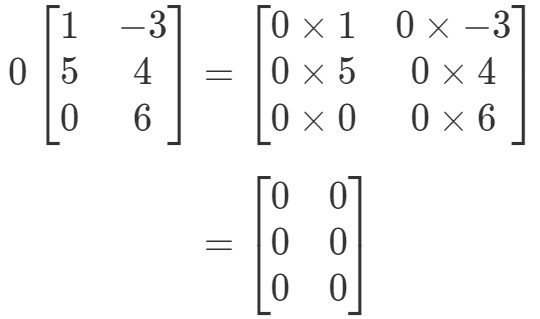
Lägg märke till att alla poster i matrisen är 0. Detta är känt som en nollmatris som är 3 x 2.

Nu när vi är väl förtrogna med skalär multiplikation, varför går vi inte över till matrismultiplikation?

Hur man multiplicerar matriser

För att multiplicera en matris med en annan matris måste vi först lära oss vad punktprodukt är.

Vad är punktprodukt?

Punktprodukt (även känd som vektormultiplikation) är ett sätt att beräkna produkten av två vektorer. Låt till exempel de två vektorerna vara:

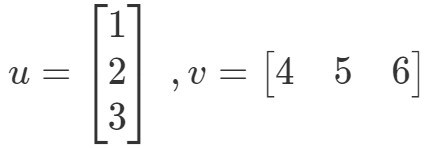
Hur skulle jag multiplicera dessa två vektorer? Helt enkelt bara multiplicera motsvarande poster och addera produkterna tillsammans. Med andra ord,

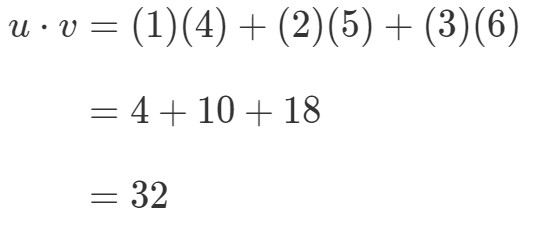
Så vi får ett enda värde genom att multiplicera vektorerna. Lägg dock märke till att de två vektorerna har samma antal poster, men vad händer om en av vektorerna har ett annat antal poster än den andra? Till exempel, låt

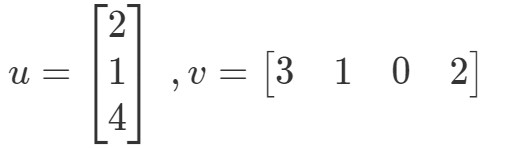
Om jag skulle multiplicera motsvarande poster och addera dem alla tillsammans får jag:

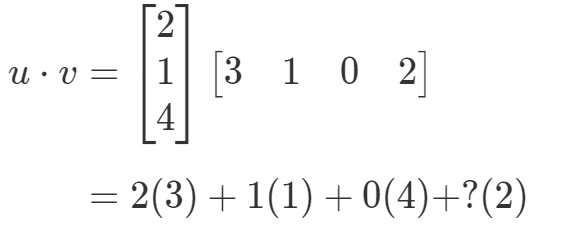
Det finns ett problem här. De tre första posterna har motsvarande poster att multiplicera med, men inte den sista posten. Så vad gör vi här? Svaret är att vi inte kan göra någonting här. Det betyder bara att vi inte kan beräkna punktprodukten av dessa två vektorer.

Så sammanfattningsvis kan vi inte hitta punktprodukten av två vektorer som har olika antal poster. De måste ha samma antal poster.

2 x 2 matrismultiplikation

Så vad var poängen med att lära sig punktprodukten? Jo, vi kommer att använda punktprodukten när vi multiplicerar två matriser med varandra. När vi multiplicerar en matris med en annan matris vill vi behandla rader och kolumner som en vektor. Mer specifikt vill vi behandla varje rad i den första matrisen som vektorer och varje kolumn i den andra matrisen som vektorer. Låt oss göra ett exempel.

Fråga 3: Hitta A∙BA \bullet BA∙B if

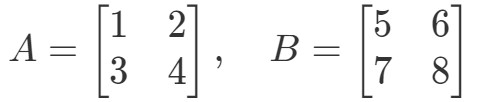
Multiplicering av de två matriserna ger oss:

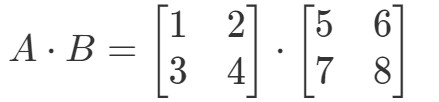
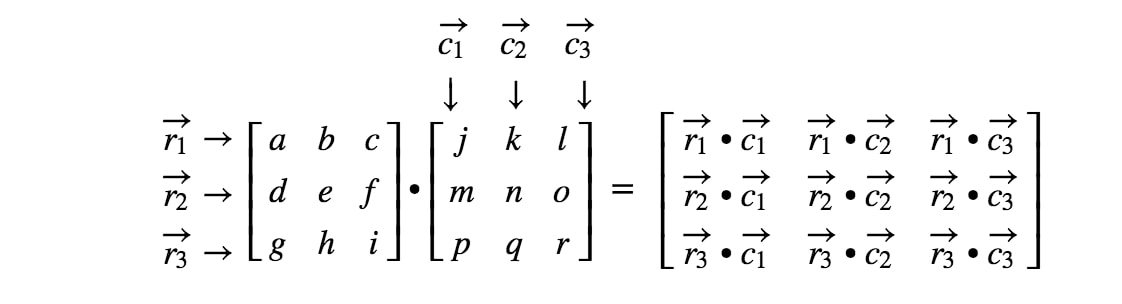
Nu är de rader och kolumner som vi fokuserar på

där r1r_{1}r1 är den första raden, r2r_{2}r2 är den andra raden och, c1,c2c_{1}, c_{2}c1,c2 är första och andra kolumnen. Nu kommer vi att behandla varje rad och kolumn vi ser här som en vektor.

Bemärk här att multiplicering av en 2 x 2-matris med en annan 2 x 2-matris ger en 2 x 2-matris. Med andra ord ska matrisen vi får ha 4 poster.

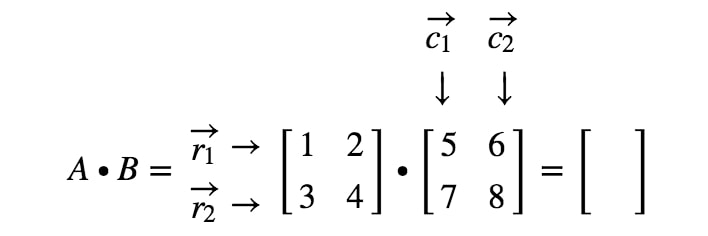
Hur får vi exakt fram den första posten? Jo, lägg märke till att den första posten finns på den första raden och den första kolumnen. Så vi tar helt enkelt punktprodukten av r1r_{1}r1 och c1c_{1}c1. Den första posten blir alltså

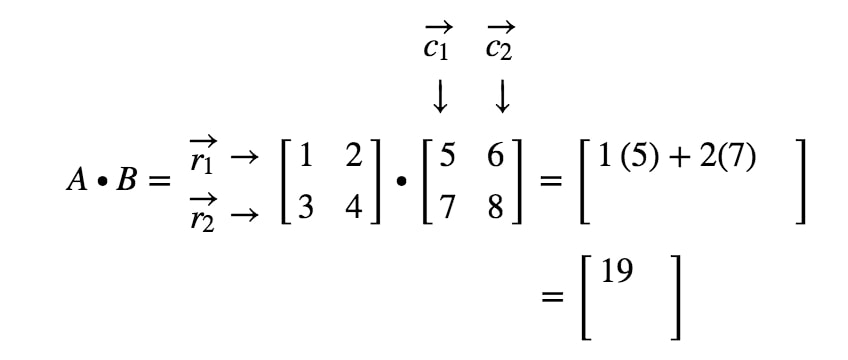
Hur får vi fram den andra posten den här gången? Lägg märke till att platsen för den andra posten ligger i första raden och andra kolumnen. Så vi tar helt enkelt punktprodukten av r1r_{1}r1 och c2c_{2}c2. Den andra posten blir alltså

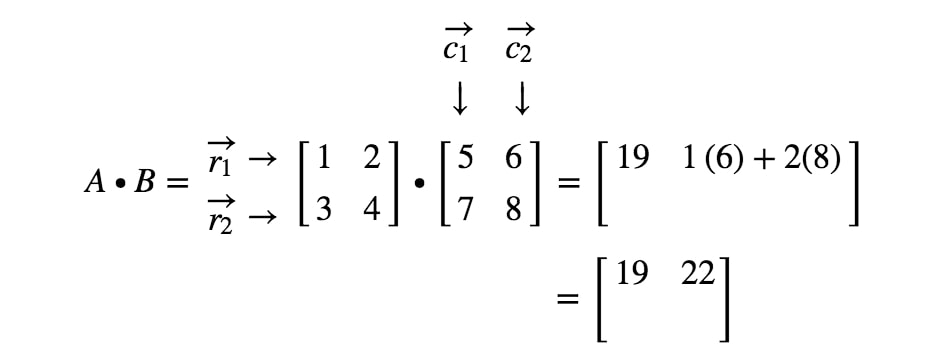
Nu ska vi använda samma strategi för att leta efter de två sista posterna. Lägg märke till att den näst sista posten ligger i 2nd2^{nd}2nd row och 1st1^{st}1st column, och den sista posten ligger i 2nd2^{nd}2nd row och 2nd2^{nd}2nd column. Vi tar alltså punktprodukten av r2r_{2}r2 och c1c_{1}c1, och punktprodukten av r2r_{2}r2 och c2c_{2}c2. Detta ger oss:

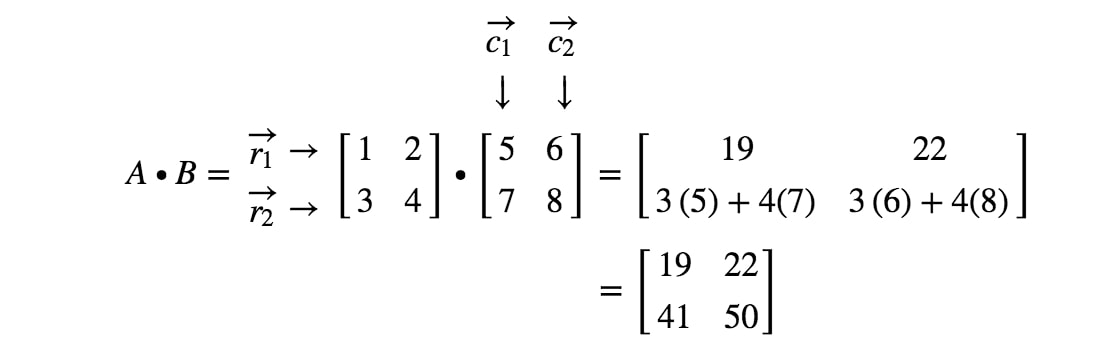
Nu är vi klara! Detta är vad vi får när vi multiplicerar 2 x 2 matriser. I allmänhet är matrismultiplikationsformeln för 2 x 2-matriser

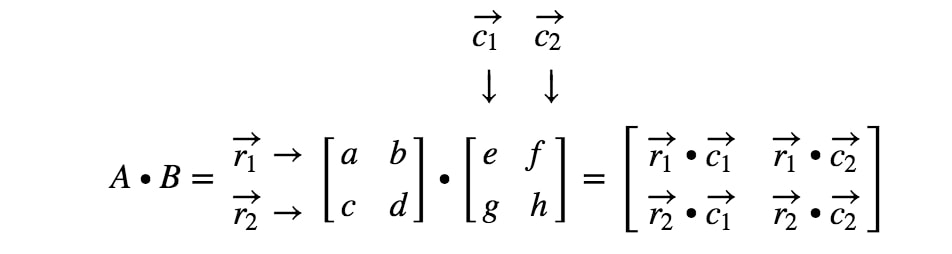
3×3-matrismultiplikation

Nu liknar processen för en 3 x 3-matrismultiplikation mycket processen för en 2 x 2-matrismultiplikation. Återigen, varför gör vi inte ett exempel på en matrismultiplikation?

Fråga 4:Hitta A∙BA \bullet BA∙B if

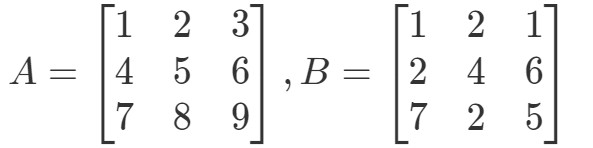
För det första, lägg märke till att om vi multiplicerar dem så borde det ge oss ytterligare en 3 x 3-matris. Med andra ord,

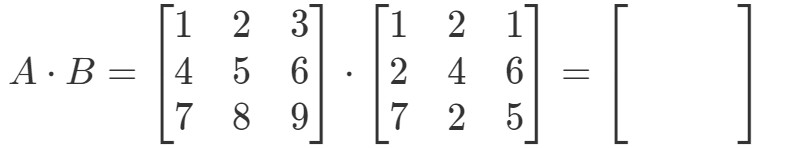
Nu ska vi märka alla våra rader i den första matrisen och kolumnerna i den andra matrisen.

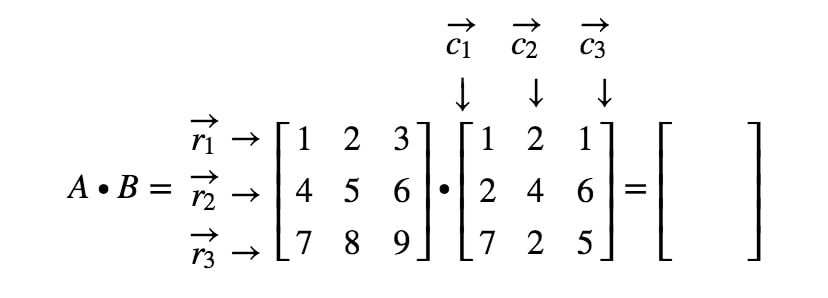
Bemärk att den första posten i matrisen ligger i 1:a^{st}1:a raden och 1:a^{st}1:a kolumnen, så vi tar punktprodukten av r1r_{1}r1 och c1c_{1}c1. Detta ger oss:

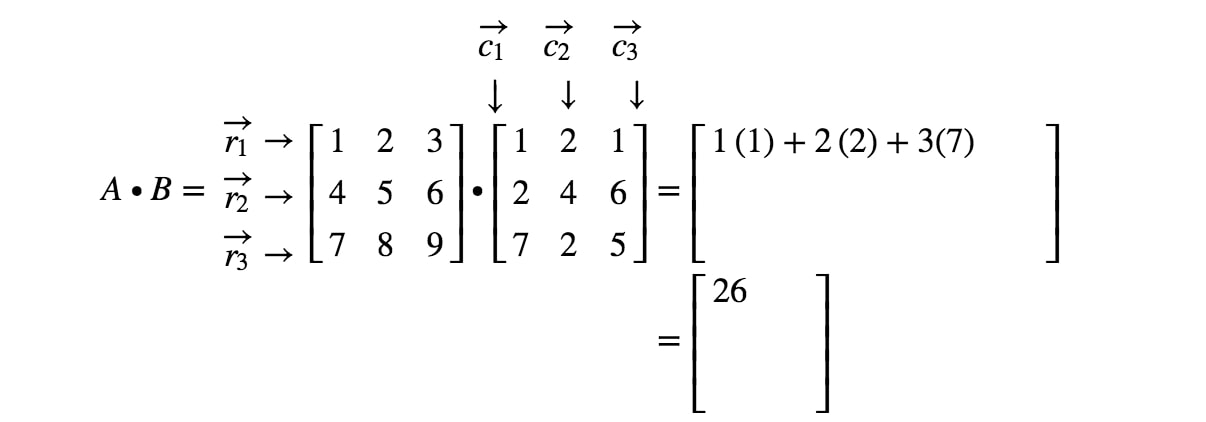
Märk nu att den andra posten i matrisen är belägen i 1:a^{st}1:a raden och 2:a^{st}2:a kolumnen. Vi tar alltså punktprodukten av r1r_{1}r1 och c2c_{2}c2. Detta ger oss:

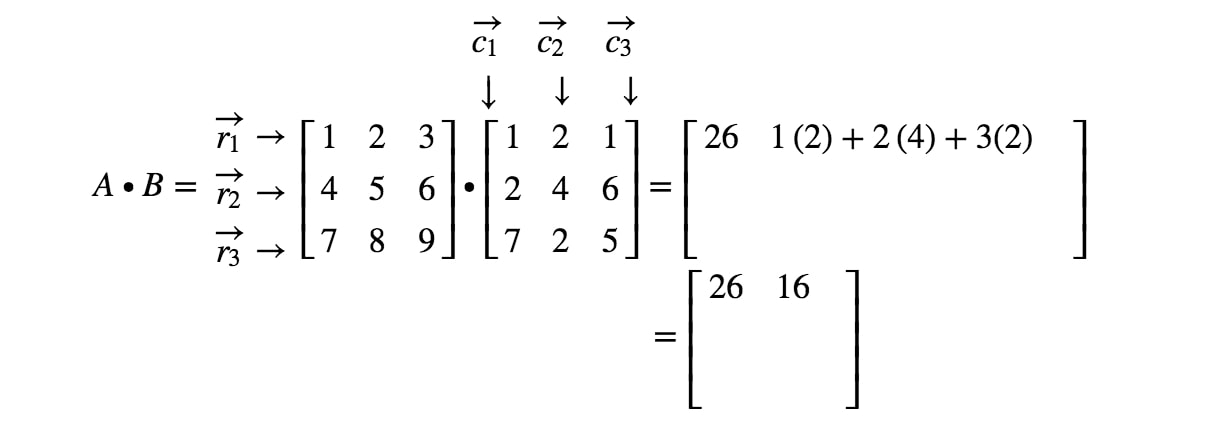
Om vi ska fortsätta att lokalisera alla poster och göra punktprodukten som motsvarar raderna och kolumnerna får vi slutresultatet:

Vi är klara! Lägg märke till att ju större matriserna är, desto tråkigare blir matrismultiplikationen. Detta beror på att vi måste hantera fler och fler tal! I allmänhet är matrismultiplikationsformeln för 3 x 3-matriser

Hur multiplicerar man matriser med olika dimensioner?

Här långt har vi multiplicerat matriser med samma dimensioner. Dessutom vet vi att om man multiplicerar två matriser med samma dimension får man en matris med samma dimensioner. Men vad händer om vi multiplicerar en matris med olika dimensioner? Hur kan vi veta vilka dimensioner den beräknade matrisen har? Först måste vi se att multiplikation av matriserna ger en definierad matris.

Är matrisen definierad?

Det finns fall där det inte är möjligt att multiplicera två matriser tillsammans. I dessa fall kallar vi matrisen för odefinierad. Hur kan vi se om de är odefinierade?

Produkten av två matriser är endast definierad om antalet kolumner i den första matrisen är lika med antalet rader i den andra matrisen.

Låt oss försöka använda den här definitionen i det här exemplet.

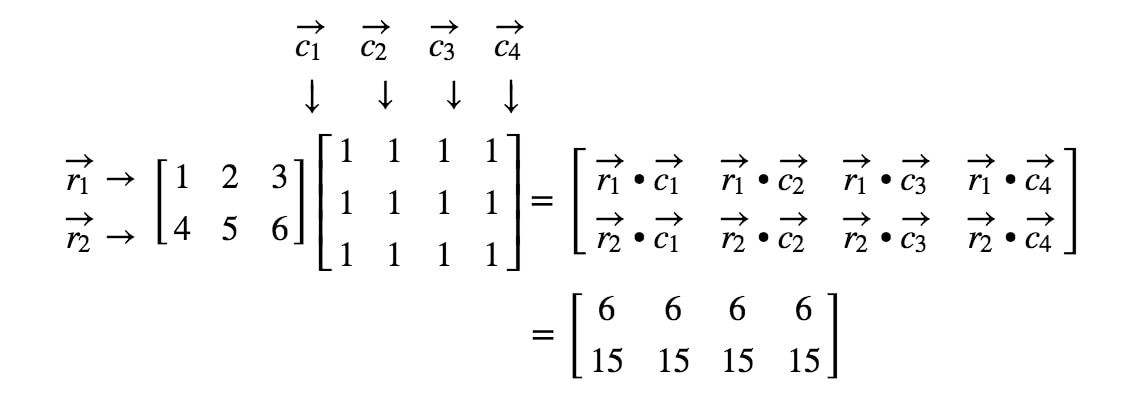
Fråga 5: Låt

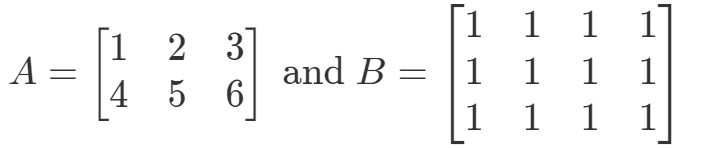
Är A∙BA \bullet BA∙B definierad?

Först ska du notera att den första matrisen har tre kolumner. Dessutom har den andra matrisen 3 rader. Eftersom båda är lika med 3 vet jag att A∙BA \bullet BA∙B är definierad.

När vi nu vet att den är definierad, hur skulle vi då kunna veta måtten på A∙BA \bullet BA∙B?

Dimensionens egenskap

För att hitta dimensionerna hos A∙BA \bullet BA∙B måste vi först titta på dimensionerna hos och separat.

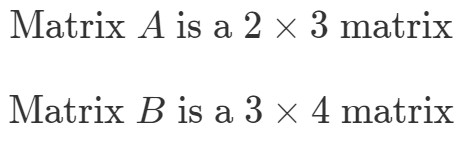
Nu ska vi ställa dimensionerna av matriserna sida vid sida så här:

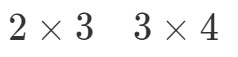
Vad vi ska göra nu är att ta det första numret och det sista numret och kombinera dem för att få dimensionerna av A∙BA \bullet BA∙B. Se att det första numret är 2 och det sista numret är 4. Så dimensionerna för A∙BA \bullet BA∙B blir:

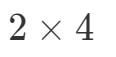
När vi nu känner till matrisens dimensioner kan vi bara beräkna varje post genom att använda punktprodukterna. Detta ger oss:

Nu när vi vet hur man multiplicerar matriser på ett bra sätt, varför inte ta en titt på några regler för matrismultiplikation?

Matrismultiplikationsegenskaper

Vad för typ av egenskaper har matrismultiplikation egentligen? Låt oss först formellt definiera allting.

Låt X,Y,ZX, Y, Y, ZX,Y,Z vara matriser, InI_{n}In vara en identitetsmatris och OnO_{n}On vara en nollmatris. Om alla dessa fem matriser har samma dimensioner har vi följande egenskaper för matris till matrismultiplikation:

Den associativa egenskapen säger att det inte spelar någon roll i vilken ordning man multiplicerar. Med andra ord, att beräkna X∙YX \bullet YX∙Y och sedan multiplicera med ZZZ skulle ge dig samma resultat som att beräkna Y∙ZY \bullet ZY∙Z och sedan multiplicera med XXX. Låt oss göra ett exempel.

Fråga 6: Visa att den associativa egenskapen fungerar med dessa matriser:

Om vi tittar på den vänstra sidan av ekvationen i den associativa egenskapen ser vi att (XY)Z(XY)Z(XY)Z(XY)Z ger:

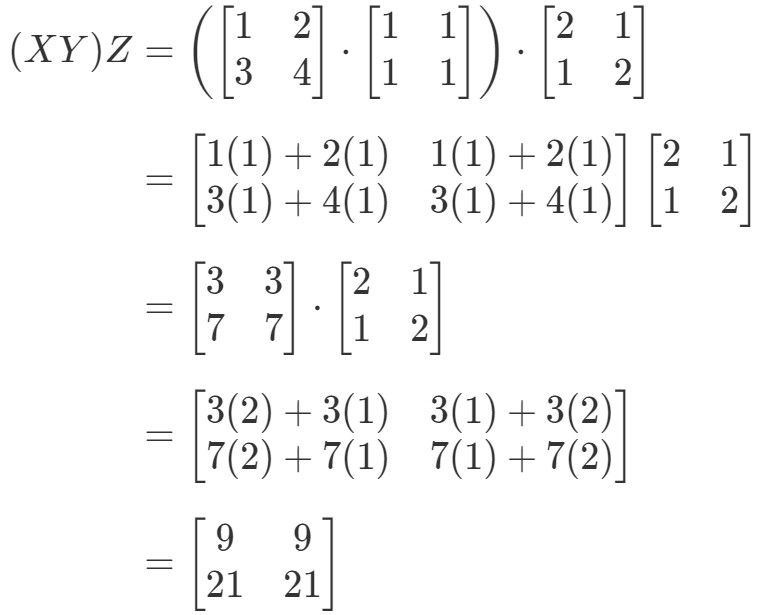
Om vi nu tittar på ekvationens högra sida i den associativa egenskapen ser vi att X(YZ)X(YZ)X(YZ)X(YZ) ger:

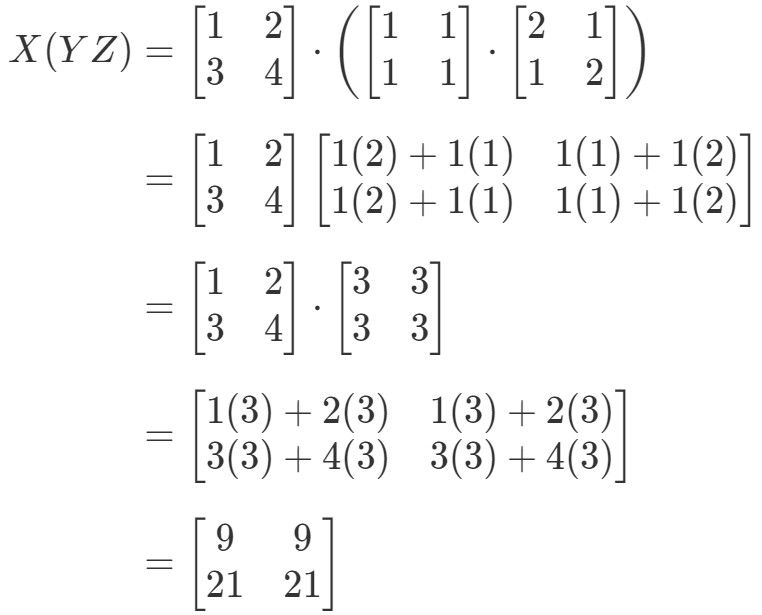
Se hur ekvationens vänstra sida och högra sida båda är lika. Därmed vet vi att den associativa egenskapen faktiskt fungerar! Återigen innebär detta att matrisens multiplikationsordning inte spelar någon roll!

Nu är nästa egenskap den distributiva egenskapen. Den distributiva egenskapen säger att:

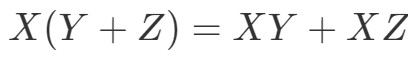
Vi ser att vi får använda folietekniken även för matriser. Bara för att visa att denna egenskap fungerar, låt oss göra ett exempel.

Fråga 7: Visa att den distributiva egenskapen fungerar för följande matriser:

Visa att den vänstra sidan av ekvationen är X(Y+Z)X(Y+Z)X(Y+Z)X(Y+Z). Att beräkna det ger alltså:

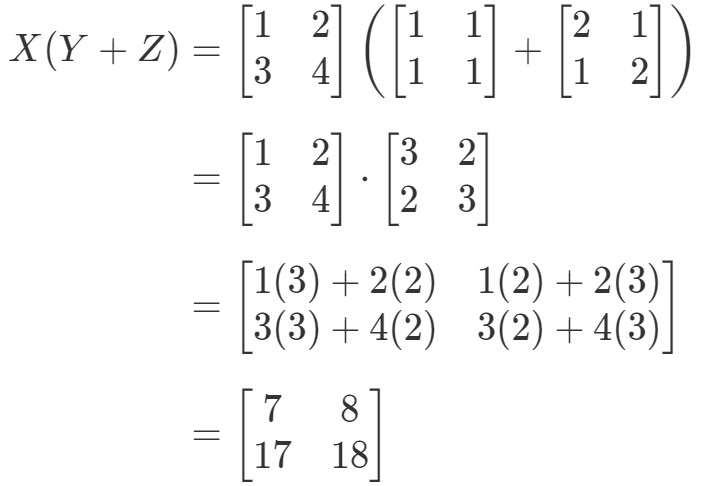
Nu ska vi kontrollera om ekvationens högra sida ger oss exakt samma sak. Lägg märke till att ekvationens högra sida är XY+XZXY + XZXY+XZ. Att beräkna detta ger oss:

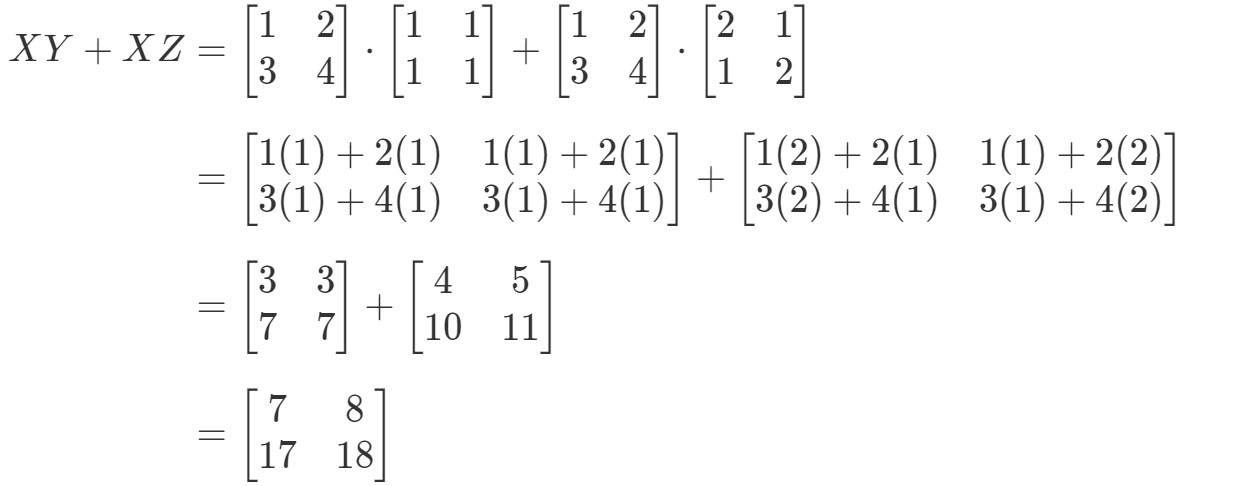
Bemärk att ekvationens vänstra sida är exakt samma sak som ekvationens högra sida. Därför kan vi bekräfta att den distributiva egenskapen faktiskt fungerar.

Är matrismultiplikation kommutativ?

Vi vet att matrismultiplikation uppfyller både den associativa och den distributiva egenskapen, men vi talade inte alls om den kommutativa egenskapen. Betyder det att matrismultiplikation inte uppfyller den? Det gör den faktiskt inte, och vi kan kontrollera det med ett exempel.

Fråga 8: Om matrismultiplikation är kommutativ måste följande vara sant:

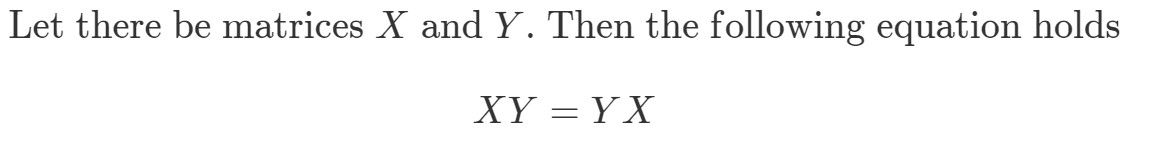
Visa att XYeqYXXY eq YXXYeqYX om

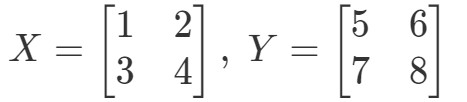
Först beräknar vi vänstersidan av ekvationen. Genom att beräkna XYXYXY får vi:

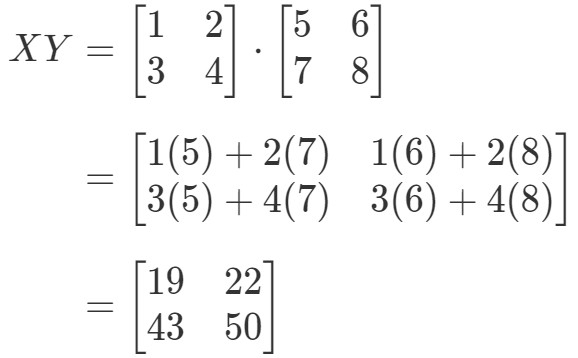
När vi nu beräknar ekvationens högra sida får vi:

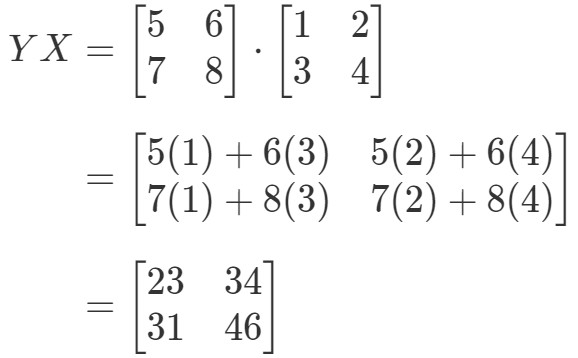
Som du kan se,

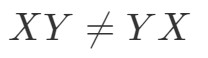
För att vi har

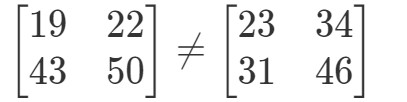
De här två matriserna är helt olika.

Nu återstår ytterligare några egenskaper för multiplikation av matriser. Dessa egenskaper behandlar dock noll- och identitetsmatriserna.

Matrismultiplikation för nollmatrisen

Matrismultiplikationsegenskapen för nollmatrisen säger följande:

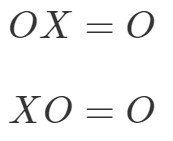
där OOO är en nollmatris.

Detta innebär att om du multiplicerar en nollmatris med en annan matris som inte är noll, får du en nollmatris. Låt oss testa om detta stämmer med ett exempel.

Fråga 9: Visa att ekvationen OX=OOX = OOX=O och XO=OXO = OXO=O gäller om:

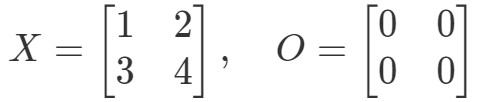
Låt oss först titta på ekvationen

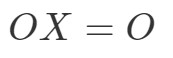
Bemärk att beräkningen av OXOXOX ger oss:

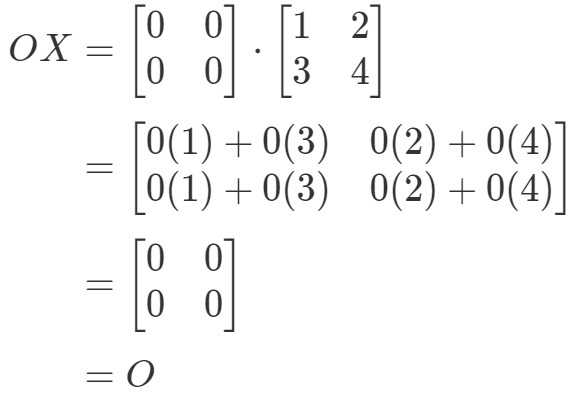
Vi ser att OX=OOX = OOX=O, så ekvationen gäller. På samma sätt får vi följande om vi beräknar XOXOXOXO:

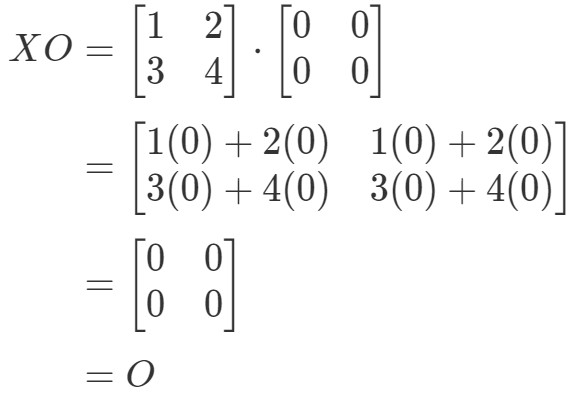
Vi ser att ekvationen XO=OXO = OXO=O håller, så vi är klara.

Matrismultiplikation för identitetsmatrisen

Hur är det nu med egenskapen matrismultiplikation för identitetsmatriser? Jo, egenskapen säger följande:

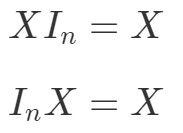
där InI_{n}In är en n×nn \ gånger nn×n identitetsmatris. Återigen kan vi se att följande ekvationer gäller med ett exempel.

Fråga 10: Visa att ekvationerna XI2=XX I_{2} = XXI2=X och I2X=XI_{2} X = XI2X=X gäller med följande matriser

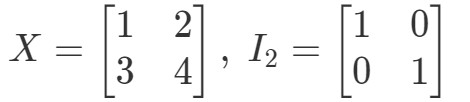
Så för ekvationen XI2=XX I_{2} = XXI2=X har vi:

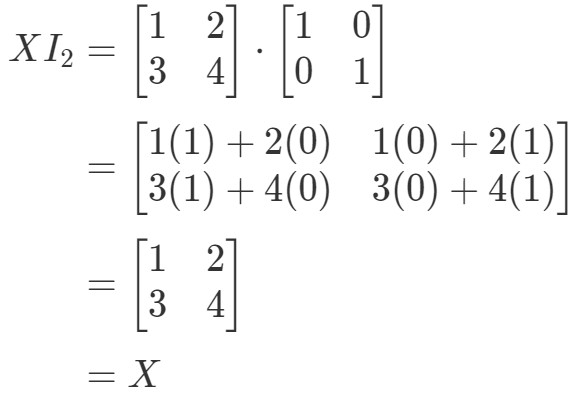
Så ekvationen gäller. I likhet med ekvationen I2X=XI_{2}X = XI2X=X har vi:

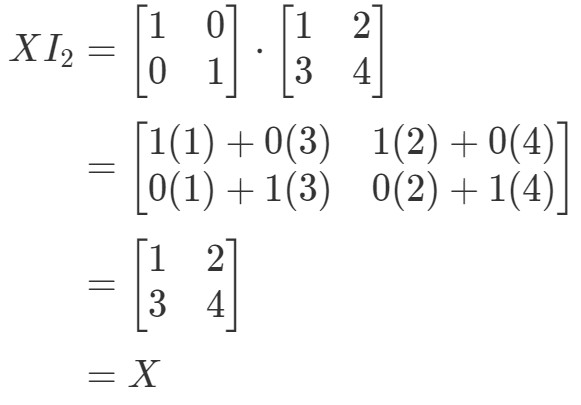
Återigen gäller ekvationen. Vi är alltså klara med frågan och båda ekvationerna är giltiga, vilket avslutar alla egenskaper för matrismultiplikation. Om du nu vill titta på en verklig tillämpning av matrismultiplikation rekommenderar jag att du tittar på den här artikeln.

https://www.mathsisfun.com/algebra/matrix-multiplying.html