Free Press

Matrixvermenigvuldiging

Er zijn precies twee manieren om matrices te vermenigvuldigen. De eerste manier is om een matrix te vermenigvuldigen met een scalair. Dit staat bekend als scalaire vermenigvuldiging. De tweede manier is een matrix te vermenigvuldigen met een andere matrix. Dat staat bekend als matrixvermenigvuldiging.

Scalaire vermenigvuldiging

Scalaire vermenigvuldiging is eigenlijk een heel eenvoudige matrixbewerking. Om een scalair met een matrix te vermenigvuldigen, nemen we eenvoudigweg de scalair en vermenigvuldigen die met elke ingang in de matrix. Laten we een voorbeeld geven.

Vraag 1: Bereken 2A2A2A als

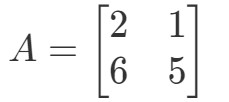
De vraag is om uit te vinden wat 2A2A2A is. Met andere woorden, we vinden

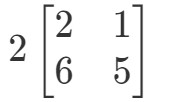
Merk op dat als we 2 vermenigvuldigen met elke ingang in de matrix, we dat krijgen:

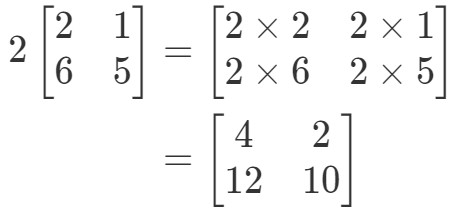
Zeer eenvoudig! Laten we er nog een doen.

Vraag 2: Bereken 0A0A0A als

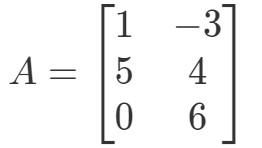
Wederom proberen we 0A0A0A0A te vinden. Dit betekent dat we op zoek gaan naar het antwoord op

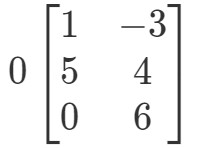
De matrix zal een vreemde vorm hebben, maar het concept blijft hetzelfde. We zullen nog steeds de scalair 0 vermenigvuldigen met elke ingang in de matrix. Dat levert op:

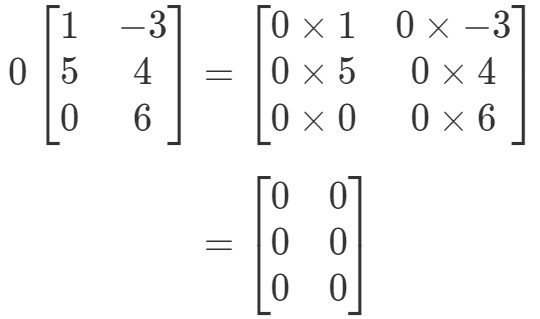
Merk op dat alle items in de matrix 0 zijn. Dit staat bekend als een nulmatrix die 3 x 2 is.

Nu we zeer vertrouwd zijn met scalaire vermenigvuldiging, waarom gaan we dan niet over op matrixvermenigvuldiging?

Hoe matrices te vermenigvuldigen

Om een matrix met een andere matrix te vermenigvuldigen, moeten we eerst leren wat een dotproduct is.

Wat is dotproduct?

Dotproduct (ook bekend als vectorvermenigvuldiging) is een manier om het product van twee vectoren te berekenen. Stel bijvoorbeeld dat de twee vectoren zijn:

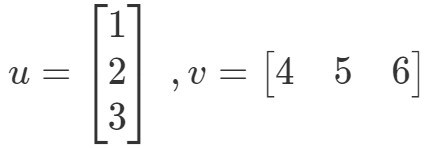
Hoe zou ik deze twee vectoren vermenigvuldigen? Gewoon de overeenkomstige waarden vermenigvuldigen, en de producten bij elkaar optellen. Met andere woorden,

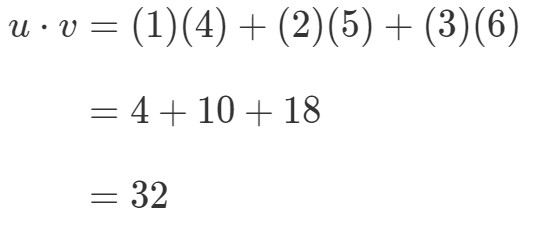
Dus we krijgen een enkele waarde door vectoren te vermenigvuldigen. Merk echter op dat de twee vectoren hetzelfde aantal ingangen hebben. Wat als een van de vectoren een ander aantal ingangen heeft dan de andere? Bijvoorbeeld, laat

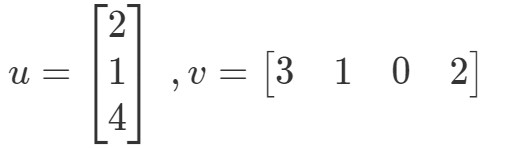
Als ik de overeenkomstige waarden vermenigvuldig en bij elkaar optel, dan krijg ik:

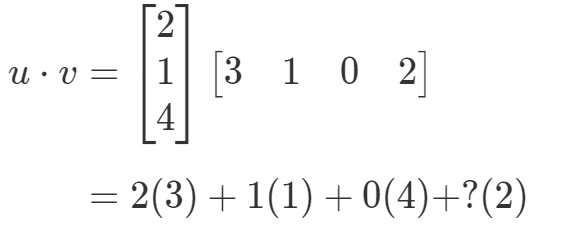
Er is hier een probleem. De eerste drie getallen hebben overeenkomstige getallen om mee te vermenigvuldigen, maar het laatste getal niet. Dus wat doen we hier? Het antwoord is dat we hier niets kunnen doen. Dit betekent alleen dat we het scalair product van deze twee vectoren niet kunnen berekenen.

Dus de conclusie is dat we het scalair product van twee vectoren met verschillende aantallen ingangen niet kunnen vinden. Ze moeten hetzelfde aantal ingangen hebben.

2 x 2 Matrixvermenigvuldiging

Waar ging het dan om bij het leren van het dotproduct? Wel, we zullen het scalair product gebruiken wanneer we twee matrices met elkaar vermenigvuldigen. Wanneer we een matrix met een andere matrix vermenigvuldigen, willen we de rijen en kolommen als een vector behandelen. Meer specifiek, we willen elke rij in de eerste matrix behandelen als vectoren, en elke kolom in de tweede matrix als vectoren. Laten we een voorbeeld geven.

Vraag 3: Vind A∙BA als

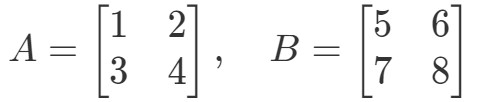
Multiplicatie van de twee matrices geeft ons:

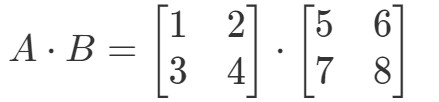
Nu zijn de rijen en de kolommen waarop we ons richten

waarin r1r_{1}r1 de eerste rij is, r2r_{2}r2 de tweede rij is, en, c1,c2c_{1}, c_{2}c1,c2 de eerste en tweede kolom zijn. Nu gaan we elke rij en kolom die we hier zien behandelen als een vector.

Merk hier op dat vermenigvuldiging van een 2 x 2 matrix met een andere 2 x 2 matrix een 2 x 2 matrix oplevert. Met andere woorden, de matrix die we krijgen moet 4 ingangen hebben.

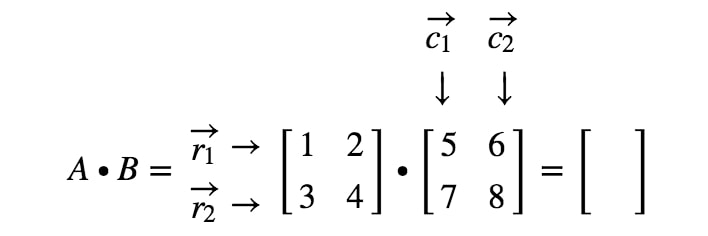
Hoe komen we precies aan de eerste ingang? Wel, merk op dat het eerste gegeven zich op de eerste rij en eerste kolom bevindt. We nemen dus gewoon het scalair product van r1r_{1}r1 en c1c_{1}c1. De eerste uitkomst is dus

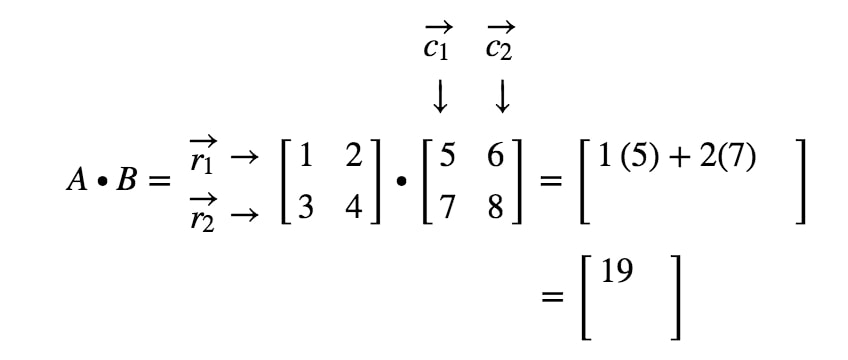
Hoe krijgen we deze keer de tweede uitkomst? Merk op dat het tweede gegeven zich in de eerste rij en de tweede kolom bevindt. We nemen dus gewoon het scalair product van r1r_{1}r1 en c2c_{2}c2. De tweede positie wordt dus

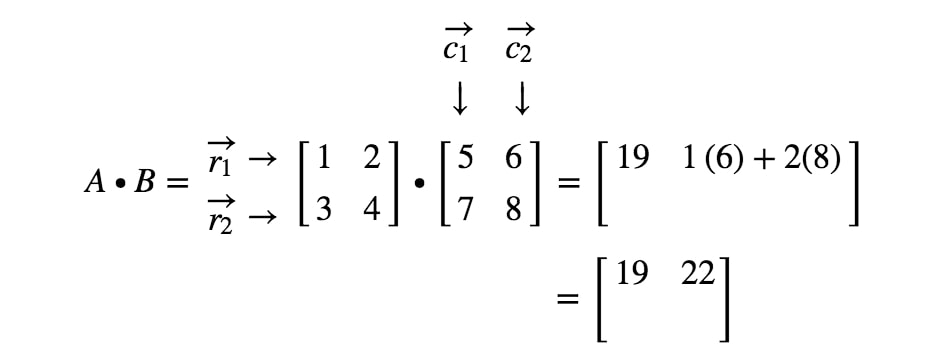
Nu gaan we dezelfde strategie gebruiken om de laatste twee posities te zoeken. Merk op dat de op een na laatste vermelding zich in de 2e2^{nd}2e rij en 1e1^{st}1e kolom bevindt, en de laatste vermelding in de 2e2^{nd}2e rij en 2e2^{nd}2e kolom. We nemen dus het scalair product van r2r_{2}r2 en c1c_{1}c1, en het scalair product van r2r_{2}r2 en c2c_{2}c2. Dit geeft ons:

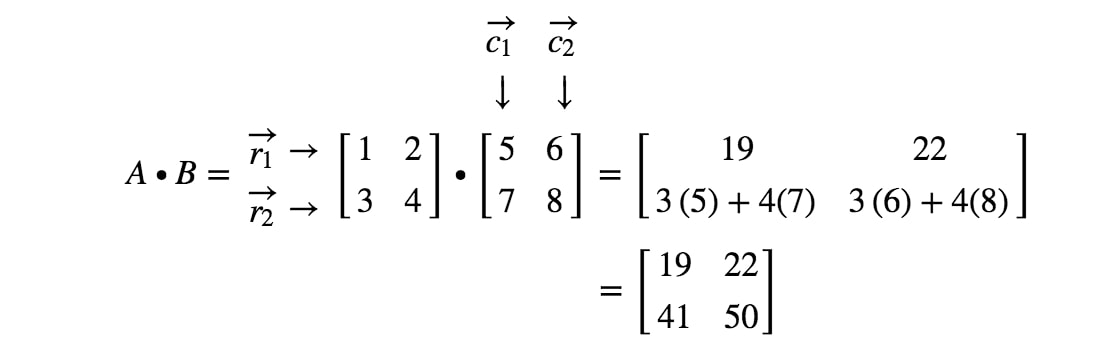
Nu zijn we klaar! Dit is wat we krijgen als we 2 x 2 matrices vermenigvuldigen. In het algemeen is de matrixvermenigvuldigingsformule voor 2 x 2 matrices

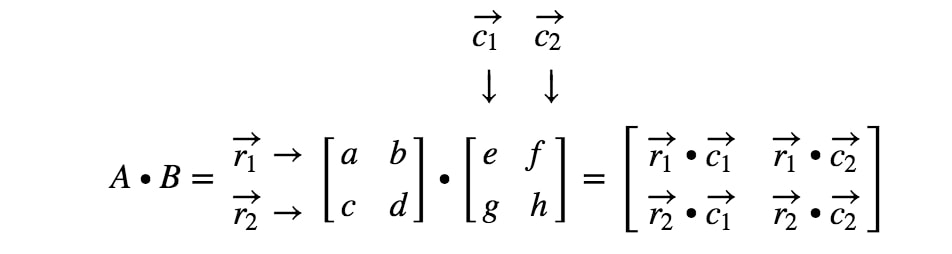
3×3 matrixvermenigvuldiging

Nu lijkt het proces van een 3 x 3 matrixvermenigvuldiging heel erg op het proces van een 2 x 2 matrixvermenigvuldiging. Nogmaals, waarom doen we geen voorbeeld van een matrixvermenigvuldiging?

Vraag 4:Vind A∙BA als

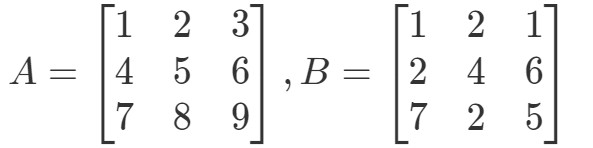
Vooreerst valt op dat vermenigvuldiging ons een andere 3 x 3 matrix moet opleveren. Met andere woorden,

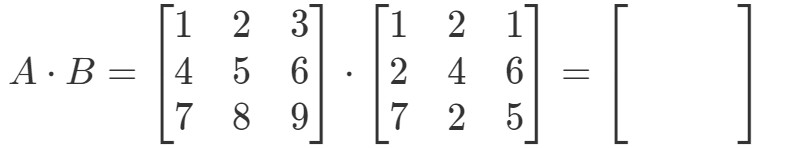
Nou, laten we al onze rijen in de eerste matrix en kolommen in de tweede matrix een label geven.

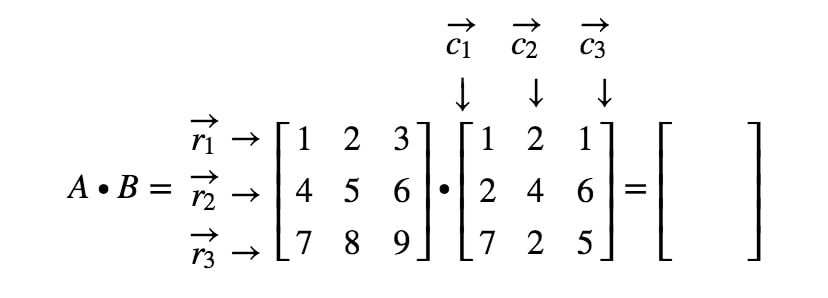
Merk op dat de eerste ingang van de matrix in de 1e1^{st}1e rij en 1e1^{st}1e kolom staat, dus nemen we het scalair product van r1r_{1}r1 en c1c_{1}c1. Dit geeft:

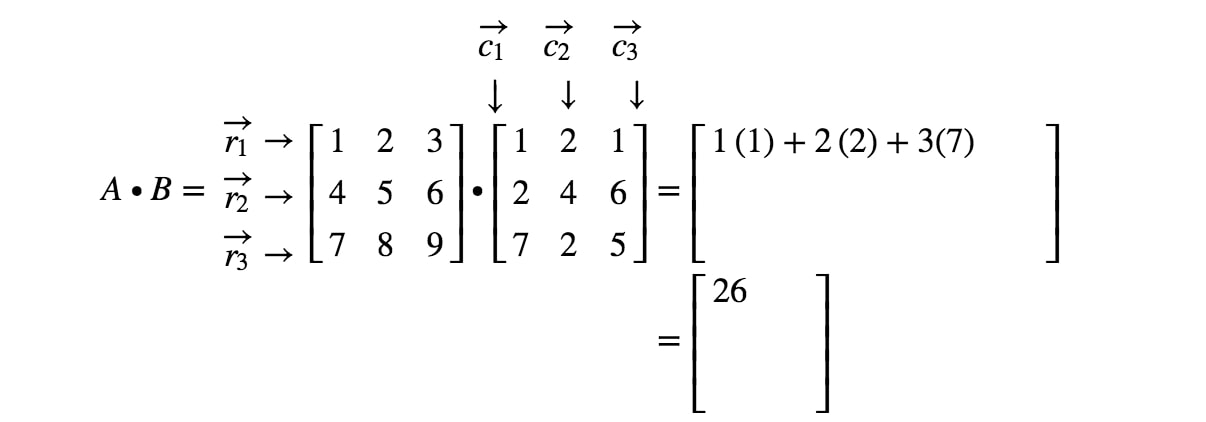
Merk nu op dat de tweede ingang van de matrix zich in de 1e1^{st}1e rij en 2e2^{nd}2e kolom bevindt. We nemen dus het scalair product van r1r_{1}r1 en c2c_{2}c2. Dit levert op:

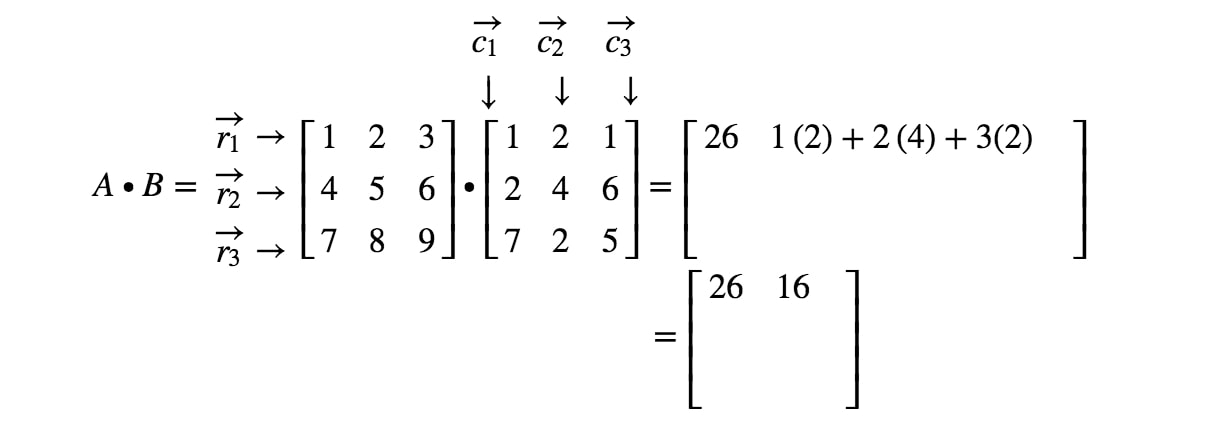
Als we alle ingangen blijven lokaliseren en het puntproduct uitvoeren dat overeenkomt met de rijen en kolommen, dan krijgen we het eindresultaat.

We zijn klaar! Merk op dat hoe groter de matrices zijn, hoe vervelender de matrixvermenigvuldiging wordt. Dit komt omdat we met steeds meer getallen te maken krijgen! In het algemeen is de matrixvermenigvuldigingsformule voor 3 x 3 matrices

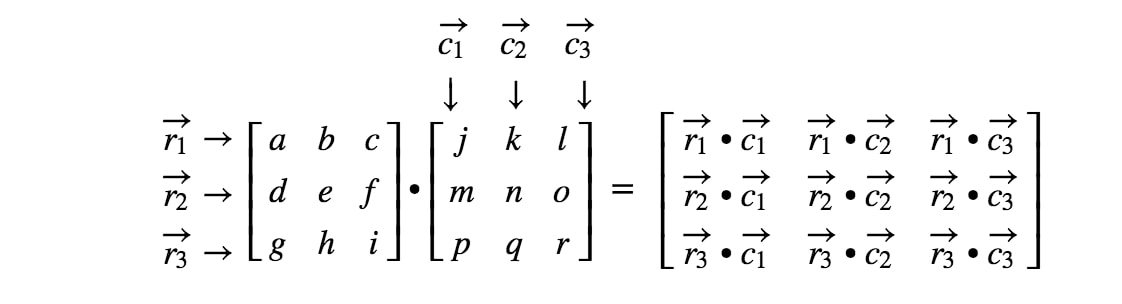
Hoe vermenigvuldig je matrices met verschillende afmetingen?

Tot nu toe hebben we matrices met dezelfde afmetingen vermenigvuldigd. Bovendien weten we dat vermenigvuldiging van twee matrices met dezelfde dimensie een matrix van dezelfde afmetingen oplevert. Maar wat gebeurt er als we een matrix met verschillende afmetingen vermenigvuldigen? Hoe weten we dan de afmetingen van de berekende matrix? Eerst moeten we zien of vermenigvuldiging van de matrices een gedefinieerde matrix oplevert.

Is de matrix gedefinieerd?

Er zijn gevallen waarin het niet mogelijk is om twee matrices met elkaar te vermenigvuldigen. In die gevallen noemen we de matrix ongedefinieerd. Hoe weten we of ze ongedefinieerd zijn?

Het product van twee matrices is alleen gedefinieerd als het aantal kolommen in de eerste matrix gelijk is aan het aantal rijen van de tweede matrix.

Laten we proberen deze definitie in dit voorbeeld te gebruiken.

Vraag 5: Laat

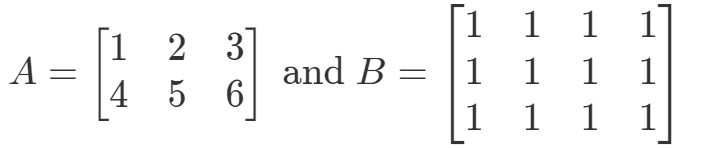
Is A∙BA ∙bullet BA∙B gedefinieerd?

Merk eerst op dat de eerste matrix 3 kolommen heeft. Ook de tweede matrix heeft 3 rijen. Omdat ze allebei gelijk zijn aan 3, weet ik dat A∙BA ∙bullet BA∙B gedefinieerd is.

Nu we weten dat hij gedefinieerd is, hoe zouden we dan de afmetingen van A∙BA ∙bullet BA∙B kunnen weten?

De dimensie-eigenschap

Om de afmetingen van A∙BA \bullet BA∙B te vinden, moeten we eerst de afmetingen van en afzonderlijk bekijken.

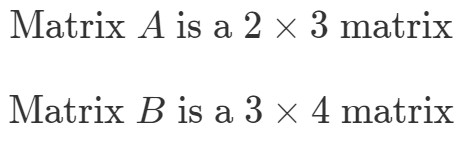
Nu gaan we de afmetingen van de matrices zo naast elkaar zetten:

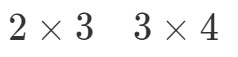
Wat we nu gaan doen is het eerste getal en het laatste getal nemen en die combineren om de afmetingen te krijgen van A∙BA ∙Bullet BA∙B. Zie dat het eerste getal 2 is en het laatste getal 4. Dus de afmetingen van A∙BA ∙bullet BA∙B worden:

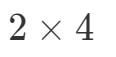
Nu we de afmetingen van de matrix weten, kunnen we gewoon elk gegeven berekenen met behulp van de puntproducten. Dit geeft ons:

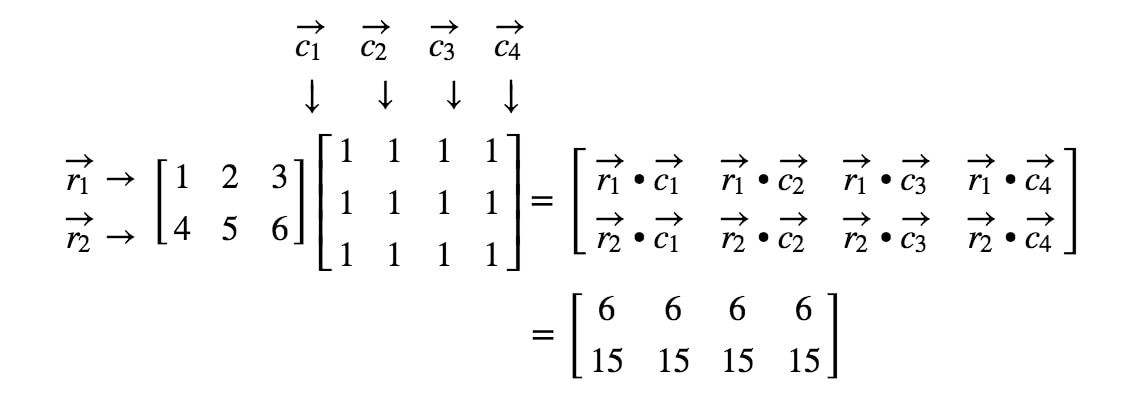
Nu we goed weten hoe we matrices kunnen vermenigvuldigen, waarom kijken we niet eens naar enkele matrixvermenigvuldigingsregels?

Eigenschappen van matrixvermenigvuldiging

Wat voor eigenschappen heeft matrixvermenigvuldiging eigenlijk? Laten we eerst alles formeel definiëren.

Laat X,Y,ZX, Y, ZX,Y,Z matrices zijn, InI_{n}In een identiteitsmatrix, en OnO_{n}On een nulmatrix. Als al deze vijf matrices even groot zijn, dan hebben we de volgende eigenschappen voor matrixvermenigvuldiging:

De associatieve eigenschap stelt dat de volgorde waarin je vermenigvuldigt er niet toe doet. Met andere woorden, als je X∙YX \bullet YX∙Y berekent en dan met ZZZ vermenigvuldigt, krijg je hetzelfde resultaat als wanneer je Y∙ZY \bullet ZY∙Z berekent en dan met XXX vermenigvuldigt. Laten we een voorbeeld geven.

Vraag 6: Laat zien dat de associatieve eigenschap werkt met deze matrices:

Kijken we naar de linkerkant van de vergelijking in de associatieve eigenschap, dan zien we dat (XY)Z(XY)Z(XY)Z geeft:

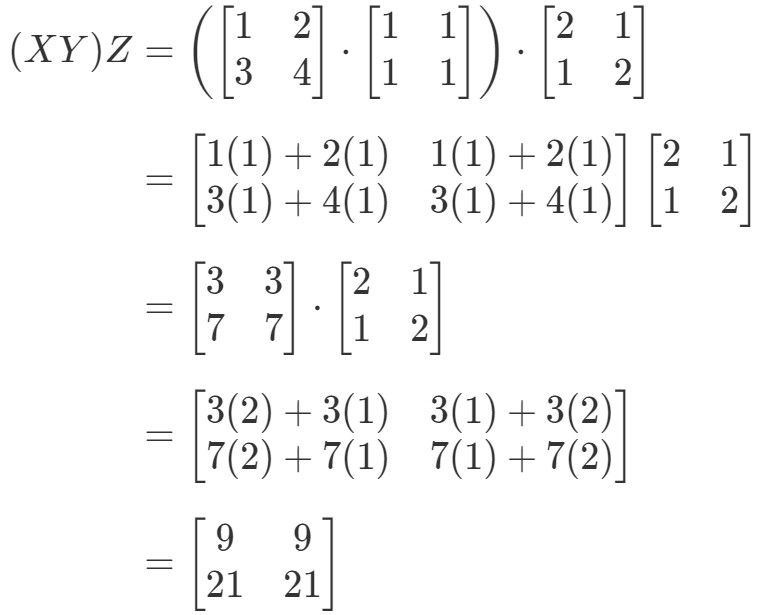
Kijken we nu naar de rechterkant van de vergelijking in de associatieve eigenschap, dan zien we dat X(YZ)X(YZ)X(YZ) geeft:

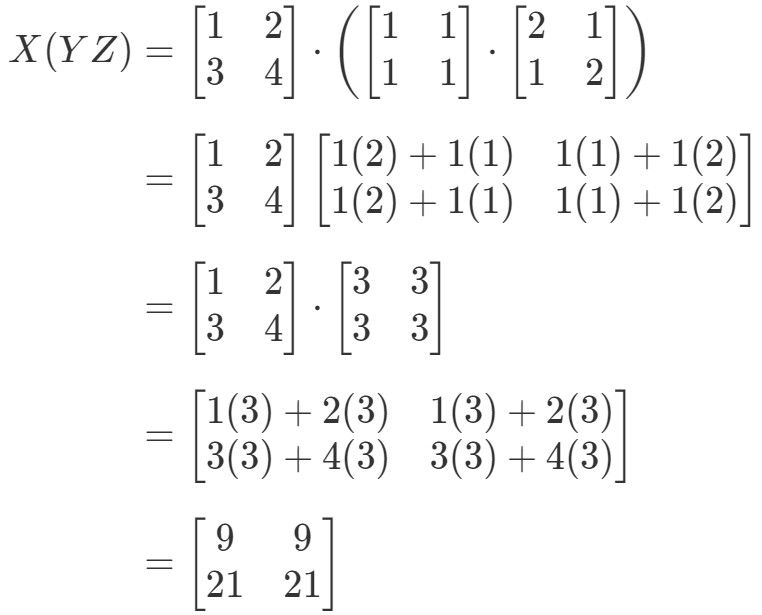
Zien we hoe de linkerkant en de rechterkant van de vergelijking beide gelijk zijn. We weten dus dat de associatieve eigenschap echt werkt! Nogmaals, dit betekent dat de volgorde van de matrixvermenigvuldiging er niet toe doet!

Nu de volgende eigenschap is de distributieve eigenschap. De distributieve eigenschap stelt dat:

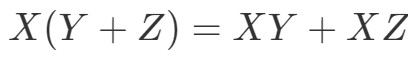
We zien dat we de folietechniek ook voor matrices mogen gebruiken. Om te laten zien dat deze eigenschap werkt, doen we een voorbeeld.

Vraag 7: Laat zien dat de distributieve eigenschap werkt voor de volgende matrices:

Zie dat het linkerlid van de vergelijking X(Y+Z)X(Y + Z)X(Y+Z) is. Als we dat berekenen, krijgen we:

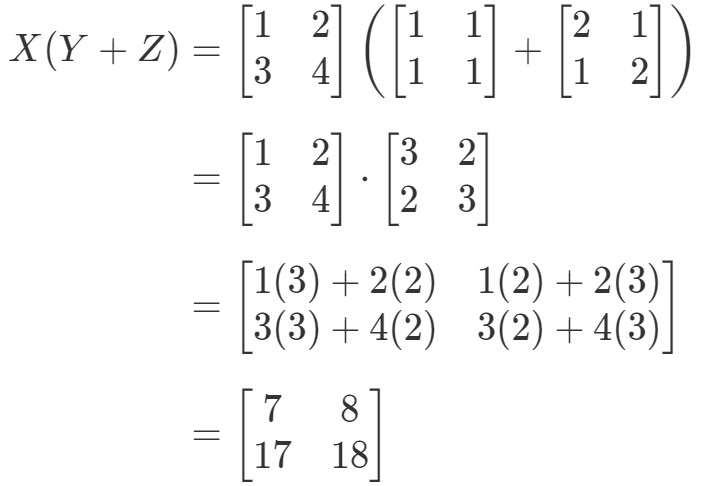
Nu gaan we kijken of het rechterlid van de vergelijking ons precies hetzelfde geeft. Merk op dat het rechterlid van de vergelijking XY+XZXY + XZXY+XZ is. Als we dit berekenen, krijgen we:

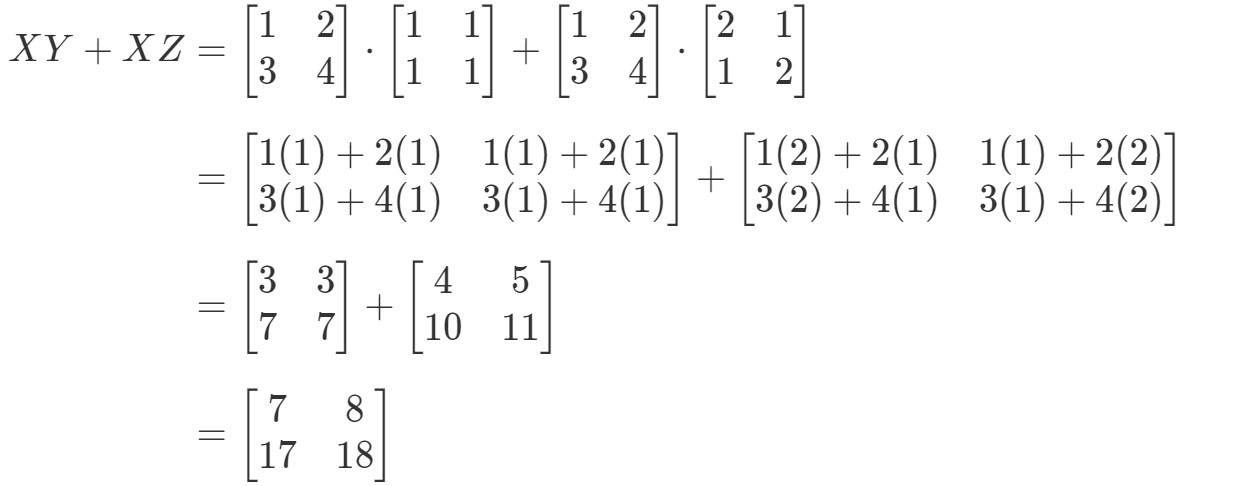
Merk op dat het linkerlid van de vergelijking precies hetzelfde is als het rechterlid van de vergelijking. We kunnen dus bevestigen dat de distributieve eigenschap inderdaad werkt.

Is matrixvermenigvuldiging commutatief?

We weten dat matrixvermenigvuldiging zowel aan de associatieve als aan de distributieve eigenschap voldoet, maar we hebben het helemaal niet gehad over de commutatieve eigenschap. Betekent dat dat matrixvermenigvuldiging daar niet aan voldoet? In feite niet, en we kunnen het controleren met een voorbeeld.

Vraag 8: Als matrixvermenigvuldiging commutatief is, dan moet het volgende waar zijn:

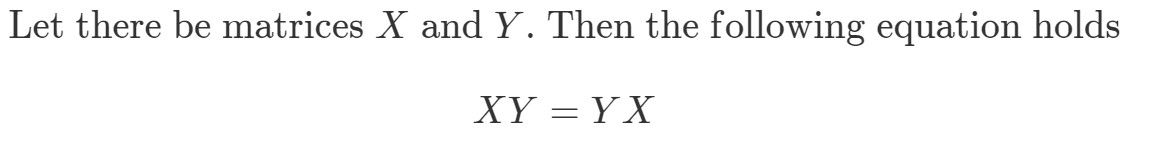
Ontdek dat XYeqYXXY eq YXXYeqYX als

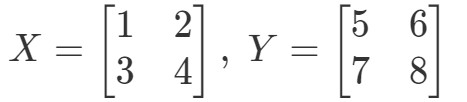
Zeerst berekenen we het linkerlid van de vergelijking. Door XYXYXY te berekenen krijgen we:

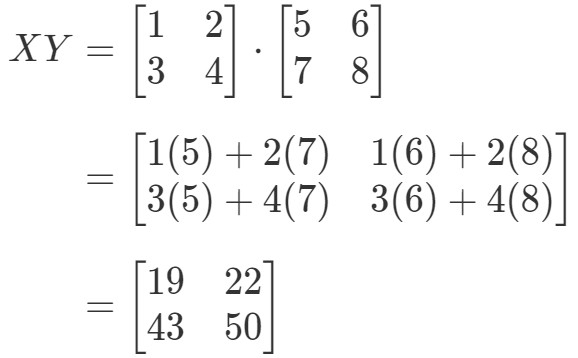
Nu berekenen we het rechterlid van de vergelijking en krijgen we:

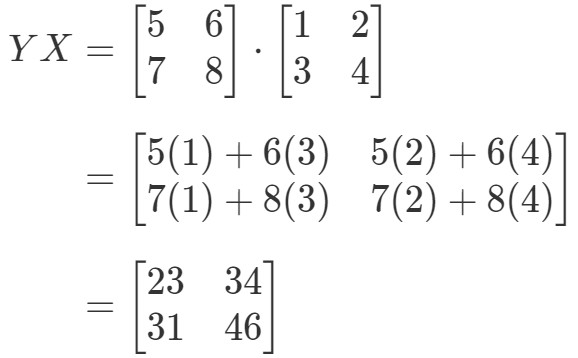
Zoals u ziet,

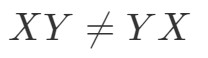
Want we hebben

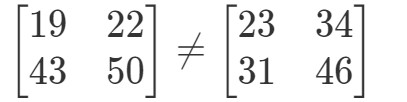
Deze twee matrices zijn totaal verschillend.

Nu zijn er nog een paar eigenschappen van de vermenigvuldiging van matrices. Deze eigenschappen hebben echter betrekking op de nul- en identiteitsmatrices.

Matrixvermenigvuldiging voor de nulmatrix

De matrixvermenigvuldigingseigenschap voor de nulmatrix luidt als volgt:

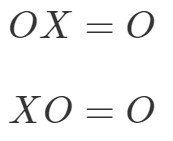
waar OOO een nulmatrix is.

Dit betekent dat als je een nulmatrix zou vermenigvuldigen met een andere matrix die niet nul is, je dan een nulmatrix krijgt. Laten we met een voorbeeld testen of dit waar is.

Vraag 9: Laat zien dat de vergelijking OX=OOX = OOX=O en XO=OXO = OXO=O geldt als:

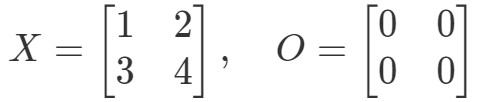
Laten we eerst eens kijken naar de vergelijking

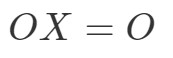
Merk op dat berekening van OXOXOX ons oplevert:

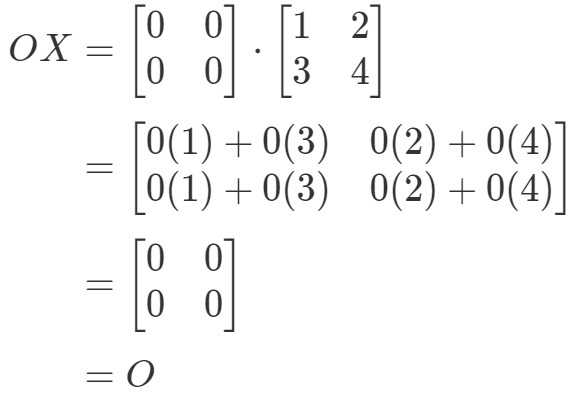
We zien dat OX=OOX = OOX=O, dus de vergelijking geldt. Op dezelfde manier, als we XOXOXO berekenen, krijgen we:

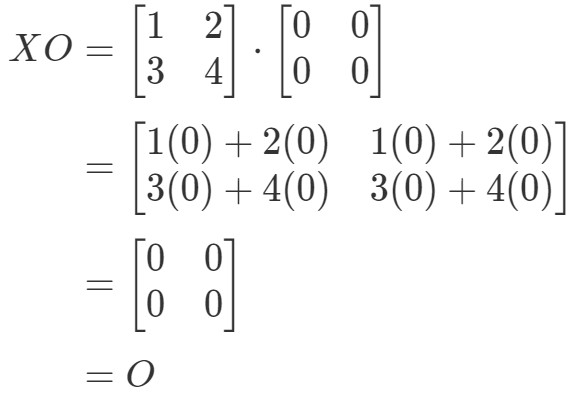
We zien dat de vergelijking XO=OXO = OXO=O geldt, dus we zijn klaar.

Matrixvermenigvuldiging voor de identiteitsmatrix

Hoe zit het nu met de matrixvermenigvuldigingseigenschap voor identiteitsmatrices? Welnu, de eigenschap stelt het volgende:

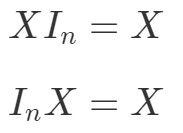
waarbij InI_{n}In een n×nn maal nn×n identiteitsmatrix is. Ook hier kunnen we met een voorbeeld zien dat de volgende vergelijkingen wel opgaan.

Vraag 10: Laat zien dat de vergelijkingen XI2=XX I_{2} = XXI2=X en I2X=XI_{2} X = XI2X=X geldt met de volgende matrices

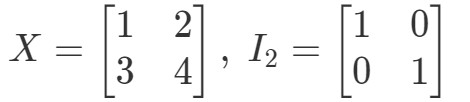
Voor de vergelijking XI2=XX I_{2} = XXI2=X geldt dus:

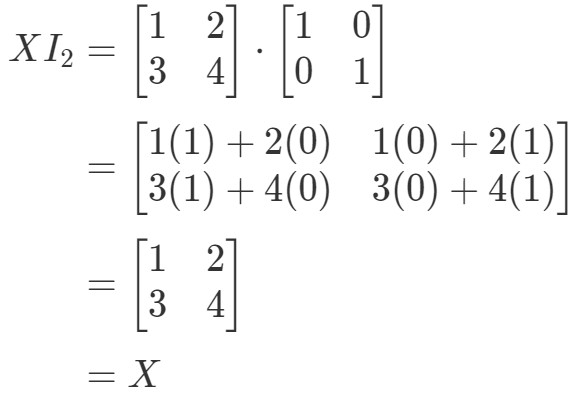
Dus de vergelijking gaat wel op. Vergelijkbaar met de vergelijking I2X=XI_{2}X = XI2X=X, hebben we:

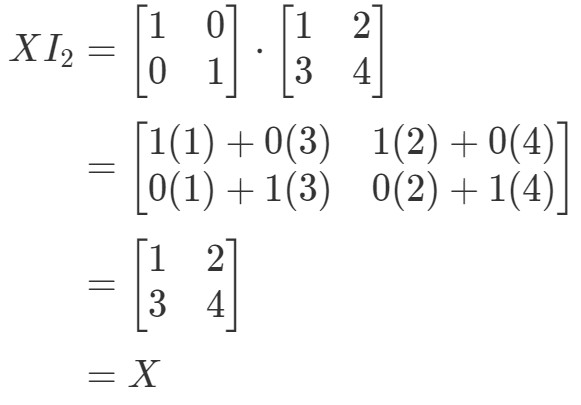
Wederom geldt de vergelijking. We zijn dus klaar met de vraag, en beide vergelijkingen zijn geldig. Hiermee zijn alle eigenschappen van matrixvermenigvuldiging opgelost. Als je nu naar een echte toepassing van matrixvermenigvuldiging wilt kijken, dan raad ik je aan dit artikel te bekijken.

https://www.mathsisfun.com/algebra/matrix-multiplying.html